探索三角形全等的条件课件北师大版七年级数学下册

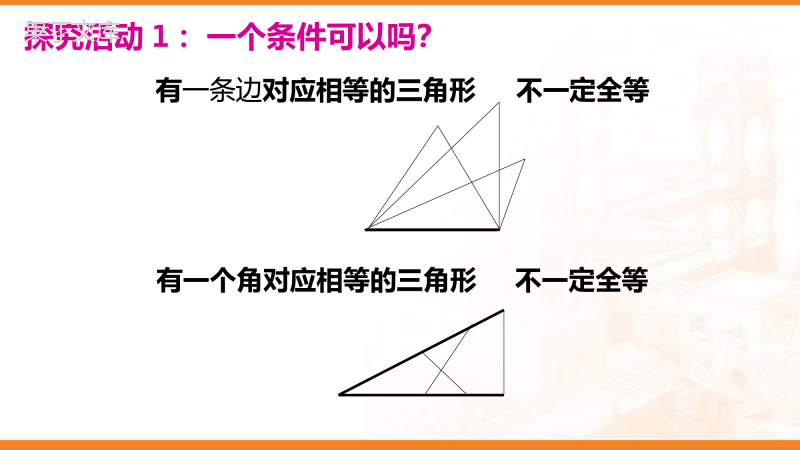
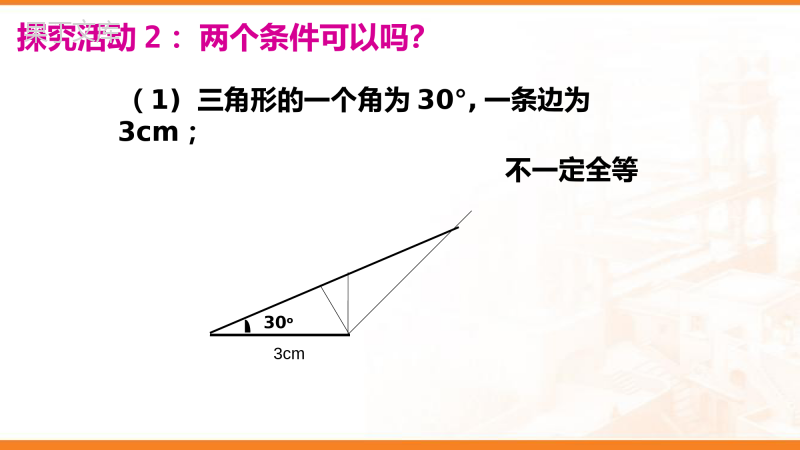
4.3.1探索三角形全等的条件ABCDEF1.什么叫全等三角形？3.已知△ABC≌△DEF，找出其中相等的边与角.2.全等三角形有什么性质？如果只满足这些条件中的一部分,那么能保证△ABC≌△DEF吗?想一想：ABCDEF有一条边对应相等的三角形不一定全等有一个角对应相等的三角形不一定全等探究活动1：一个条件可以吗？（1)三角形的一个角为30°,一条边为3cm；不一定全等30o3cm探究活动2：两个条件可以吗？(2)三角形的两个角分别是：30°，50°；不一定全等50o50o30o探究活动2：两个条件可以吗？(3)三角形的两条边分别是：4cm，6cm.不一定全等4cm4cm6cm4cm也不能保证三角形全等.两个条件你能说出有哪几种可能的情况吗？1.三个角2.三条边3.两边一角4.两角一边探究活动3：三个条件可以吗？结论:三个内角对应相等的三角形不一定全等.（1）有三个角对应相等的两个三角形60o30030060o90o90o探究活动3：三个条件可以吗？3cm4cm6cm4cm6cm3cm6cm4cm3cm（2）三边对应相等的两个三角形会全等吗？文字语言：三边对应相等的两个三角形全等.（简写为“边边边”或“SSS”）ABCDEF在△ABC和△DEF中，∴△ABC≌△DEF（SSS）.AB=DE，BC=EF，AC=DF，符号语言：边边边判定方法例1如图，有一个三角形钢架，AB=AC，AD是连接点A与BC中点D的支架．是说明：（1）△ABD≌△ACD．(2)∠BAD=∠CAD.CBDA解题思路：先找隐含条件公共边AD再找现有条件AB=AC最后找准备条件BD=CDD是BC的中点证明：∵D是BC中点，∴BD=DC．在△ABD与△ACD中，∴△ABD≌△ACD（SSS）．CBDAAB=AC(已知）BD=CD（已证）AD=AD（公共边）准备条件指明范围摆齐根据写出结论(2)∠BAD=∠CAD.由（1）得△ABD≌△ACD，∴∠BAD=∠CAD.（全等三角形对应角相等）如图,C是BF的中点，AB=DC,AC=DF.试说明:△ABC≌△DCF.BCADF在△ABC和△DCF中AB=DC∴△ABC≌△DCF(已知)(已证)AC=DFBC=CF解：∵C是BF中点∴BC=CF(已知)(SSS).已知:如图,点B、E、C、F在同一直线上,AB=DE,AC=DF,BE=CF.试说明:（1）△ABC≌DEF△；（2）∠A=∠D.解:∴△ABC≌DEF△(SSS)在△ABC和△DEF中AB=DEAC=DFBC=EF(已知)(已知)(已证)∵BE=CF∴BC=EF∴BE+CE=CF+CE（1）（2）∵△ABC≌DEF△（已证）∴∠A=∠D（全等三角形对应角相等）BCAFDEACBD解：∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC（已知）BD=CD（已证）AD=AD（公共边）∴△ABD≌△ACD（SSS）例2如图,△ABC是一个钢架，AB=AC,AD是连接A与BC中点D的支架，试说明：∠B=∠C.∴∠B=∠C由上面的结论可知，只要三角形三边的长度确定了，这个三角形的形状和大小就完全确定了.如图，将三根木条用钉子钉成一个三角形木架，然后扭动它，它的形状会改变吗？它的大小和形状是固定不变的，三角形的这个性质叫做三角形的稳定性．三角形的稳定性如图，将四根木条用钉子钉成一个四边形木架，然后扭动它，它的形状会改变吗？它的形状是可以改变的，因此四边形具有不稳定性．三角形的稳定性动手做一做1.将三根木条用钉子钉成一个三角形木架.2.将四根木条用钉子钉成一个四边形木架.三角形的稳定性1.如图，桥梁的斜拉钢索是三角形的结构，主要是为了()A.节省材料,节约成本B.保持对称C.利用三角形的稳定性D美观漂亮