探索三角形相似的条件(第2课时)(课件)-2022-2023学年九年级数学下册同步精品课堂(苏科版)

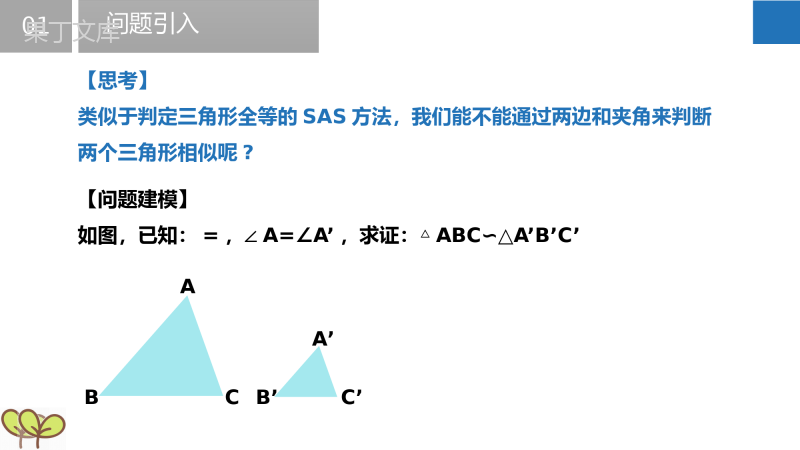
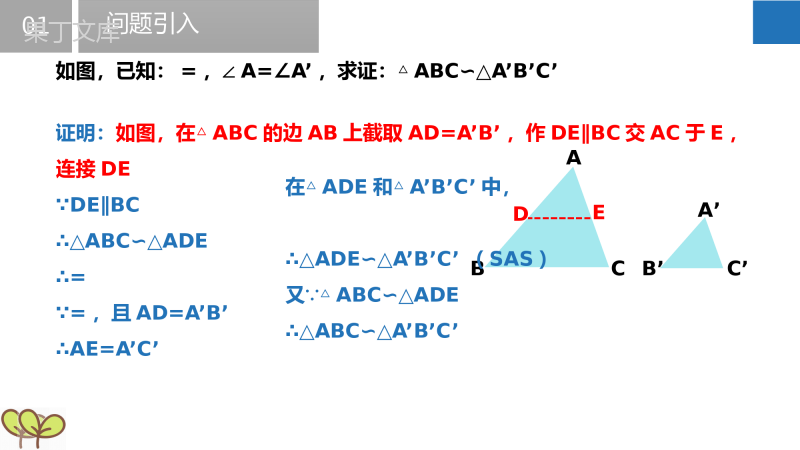
探索三角形相似的条件（下）Exploretriangularsimilarconditions苏科版九年级下册第6章图形的相似教学目标01掌握相似三角形的判定定理（二），能运用此定理证明两个三角形相似02掌握相似三角形的判定定理（三），能运用此定理证明两个三角形相似，注意区分三种判定定理使用的条件相似三角形的判定定理（二）知识精讲问题引入01【思考】类似于判定三角形全等的SAS方法，我们能不能通过两边和夹角来判断两个三角形相似呢?【问题建模】如图，已知：=，∠A=∠A’，求证：△ABC∽△A’B’C’CA’C’ABB’知识精讲问题引入01证明：如图，在△ABC的边AB上截取AD=A’B’，作DE∥BC交AC于E，连接DE∵DE∥BC∴△ABC∽△ADE∴=∵=，且AD=A’B’∴AE=A’C’如图，已知：=，∠A=∠A’，求证：△ABC∽△A’B’C’CA’C’ABB’DE在△ADE和△A’B’C’中，∴△ADE∽△A’B’C’（SAS）又∵△ABC∽△ADE∴△ABC∽△A’B’C’02知识精讲两边成比例且夹角相等的两个三角形相似.判定定理（二）由此，我们得到利用两边一夹角判定两个三角形相似的方法~∵=，∠A=∠A’∴△ABC∽△A’B’C’CA’C’ABB’02知识精讲【思考】对于△ABC和△A’B’C’，=，∠B=∠B’，这两个三角形一定相似吗？试着画画看.【结论】相等的角不是对应两边的夹角时，两个三角形不一定相似02知识精讲两边成比例且夹角相等的两个三角形相似.两边相等且夹角相等的两个三角形全等（SAS）.【再次强调】无论是证明相似or证明全等，用“两边一夹角”定理时，必须时刻警惕：相等的角必须对应两边的夹角知识精讲例1、已知：如图，AD•AB=AE•AC，求证：△ADC∽△AEB．【证明】∵AD•AB=AE•AC∴=∵∠A=∠A∴△ADC∽△AEB【两边一夹角判定相似】注意题目的隐藏条件“∠A=∠A（公共角）”知识精讲例2、如图所示，点D是△ABC的AB边上一点，且AD=1，BD=2，AC=．求证：△ACD∽△ABC．【证明】∵AD=1，BD=2，AC=∴==，=∴=∵∠A=∠A∴△ACD∽△ABC知识精讲例3、在Rt△ABC中，∠B=90°，若AB=BE=EF=FC=2．求证：△AEF∽△CEA．【证明】∵∠B=90°，AB=BE=EF=FC=2∴AE==2∴AE：EF=2：2=，CE：AE=4：2=∴AE：EF=CE：AE∵∠AEF=∠CEA∴△AEF∽△CEAagain：注意题目的隐藏条件“∠AEF=∠CEA（公共角）”知识精讲例4、如图，已知菱形ABCD，点E是AB的中点，AF⊥BC于点F，连接EF、ED、DF，DE交AF于点G，且AE2=EG•ED．求证：DE⊥EF．【证明】∵AF⊥BC，∴∠AFB=90°∵点E是AB的中点∴AE=FE，∴∠EAF=∠AFE∵AE2=EG•ED，∴=∵∠AEG=∠DEA∴△AEG∽△DEA∴∠EAG=∠ADG，∴∠AFE=∠ADG∵∠AGD=∠EGF，∴∠DAG=∠FEG∵四边形ABCD是菱形∴AD∥BC，∴∠DAG=∠AFB=90°∴∠FEG=90°，即DE⊥EF相似三角形的判定定理（三）知识精讲问题引入01【思考】类似于判定三角形全等的SSS方法，我们能不能通过两边和夹角来判断两个三角形相似呢?【问题建模】如图，已知：==，求证：△ABC∽△A’B’C’CA’C’ABB’知识精讲问题引入01证明：如图，在△ABC的边AB上截取AD=A’B’，作DE∥BC交AC于E，连接DE∵DE∥BC∴△ABC∽△ADE∴==∵==，且AD=A’B’∴DE=B’C’，EA=C’A’如图，已知：==，求证：△ABC∽△A’B’C’CA’C’ABB’DE在△ADE和△A’B’C’中，∴△ADE∽△A’B’C’（SSS）又∵△ABC∽△ADE∴△ABC∽△A’B’C’02知识精讲三边成比例的两个三角形相似.判定定理（三）由此，我们得到利用三边判定两个三角形相似的方法~∵==∴△ABC∽△A’B’C’CA’C’ABB’02知识精讲【方法总结】证明相似的方法证明全等的方法定义法1、相似定义1、全等定义判定定理法2、“两角”定理2、AAS3、ASA3、“两边一夹角”定理4、SAS4、“三边”定理5、SSS6、HL知识精讲例5、如图，△ABC和△DEF三边长已知，求证△ABC～△DEF．【证明】根据题意：==，==，==∴==∴△ABC∽△A’B’C’【三边判定相似】知识精讲例6、如图，在Rt△ABC中，∠ACB=90°，点D在AC上（1）已知：AC=4，BC=2，∠CBD=∠A，求BD的长；（2）取AB，BD的中点E，F，连接CE，EF，FC，求证：△CEF∽△BAD．【分析】（1）∵∠CBD=∠A，∠BCD=∠ACB∴△CBD∽△CAB∴=，即=∴CD=1∴BD==注意：题目条件既涉及线段长度，又涉及角相等，用“两边一夹角”定理证相似知识精讲例6、如图，在Rt△ABC中，∠ACB=90°，点D在AC上（2）取AB，BD的中点E，F，连接CE，EF，FC，求证：△CEF∽△BAD．【证明】（2）∵E、F分别是Rt△ABC、Rt△BCD斜边上的中点∴CF=BD，EC=AB又∵E、F分别为是AB、BD的中点∴EF=AD∴===∴△CEF∽△BAD注意：题目中线段比例条件，或此类条件较多时，用“三边”定理证相似02知识精讲【方法总结】判定定理使用条件“两角”定理题目中只有角相等的条件，或此类条件较多时“两边一夹角”定理题目条件既涉及线段长度（或线段比例），又涉及角相等（注意：公共角、对顶角）“三边”定理题目中只有线段长度（或线段比例）条件，或此类条件较多时知识精讲例7、如图，△ABC的两条中线，BE、CF交于点G，FE//BC，证明GB：GE=2：1.【重心与相似】【证明】如图，连接EF∵△ABC的两条中线，BE、CF交于点G，∴EF=BC，EF∥BC∴∠BCG=∠EFG∵∠BGC=∠EGF∴△BCG∽△EFG∴GB：GE=BC：EF=2：1知识精讲例8、在七年级，我们通过观察、操作，发现三角形的三条中线相交于一点.你能运用相似形的有关知识证实这个结论吗?只要再证实点G在另一条中线上根据例7，由△ABC的两条中线，BE、CF交于点G，FE//BC，可知△BCG∽△EFG，于是GB：GE=BC：EF=2：1.知识精讲如图，AD是△ABC的另一条中线，设AD、BE交于点G’，连接DE同理可得：△ABG’∽△DEG’，于是G’B：G’E=AB：DE=2：1∴点G与点G重合∴三角形的三条中线相交于一点例7、GB：GE=BC：EF=2：1例8、在七年级，我们通过观察、操作，发现三角形的三条中线相交于一点.你能运用相似形的有关知识证实这个结论吗?知识精讲∵例7、GB：GE=2：1∴GE=BE三角形的三条中线相交于一点，这点叫做三角形的重心.三角形的重心与一边中点的连线的长度是对应中线的.同理：GF=CF再同理：GD=AD课后总结11、判定定理（二）：两边成比例且夹角相等的两个三角形相似.2、判定定理（三）：三边成比例的两个三角形相似.证明相似的方法证明全等的方法定义法1、相似定义1、全等定义判定定理法2、“两角”定理2、AAS3、ASA3、“两边一夹角”定理4、SAS4、“三边”定理5、SSS6、HL判定定理使用条件“两角”定理题目中只有角相等的条件，或此类条件较多时“两边一夹角”定理题目条件既涉及线段长度（或线段比例），又涉及角相等（注意：公共角、对顶角）“三边”定理题目中只有线段长度（或线段比例）条件，或此类条件较多时课后总结21、重心的概念：三角形的三条中线相交于一点，这点叫做三角形的重心.2、重心的性质：三角形的重心与一边中点的连线的长度是对应中线的.谢谢学习Thankyouforlearning