《解一元二次方程之配方法》九年级初三数学上册PPT课件（第21.2.1课时）.pptx

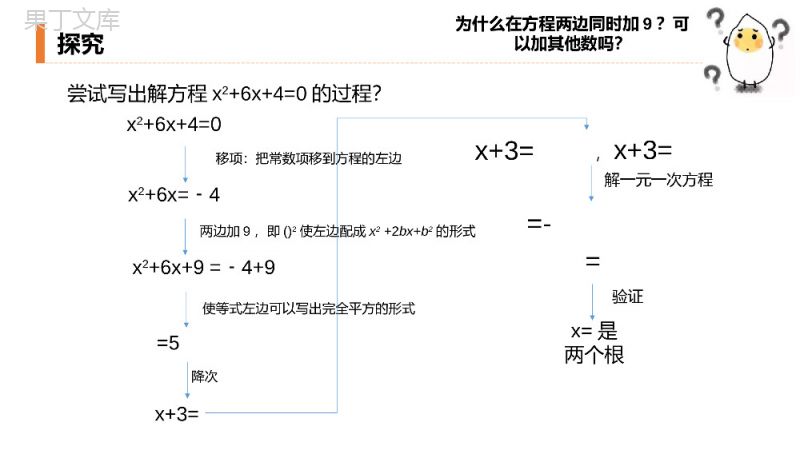
www.bangongziyuan.comTrendDesign老师：办公资源时间：2020.421.2.1解一元二次方程解一元二次方程之配方法第二十一章一元二次方程PleaseEnterYourDetailedTextHere,TheContentShouldBeConciseAndClear,ConciseAndConciseDoNotNeedTooMuchText前言学习目标1.理解配方法的概念，并运用配方法解一元二次方程。2.掌握用配方法解一元二次方程的一般步骤。重点难点重点：用配方法解一元二次方程。难点：用配方法解一元二次方程的步骤。尝试写出解方程x2+6x+4=0的过程？x2+6x+4=0移项：把常数项移到方程的左边x2+6x=4﹣两边加9，即()2使左边配成x2+2bx+b2的形式x2+6x+9=4+9﹣使等式左边可以写出完全平方的形式=5x+3=降次x+3=，x+3=解一元一次方程=-=验证x=是两个根为什么在方程两边同时加9？可以加其他数吗？探究概念：将方程通过配成完全平方形式来解一元二次方程的方法，叫做配方法.目的：关键：配方是为了降次，把一个一元二次方程转化成两个一元一次方程来解.将方程配成完全平方形式.(若方程二次项系数为1时，“方程两边加一次项系数一半的平方”)配方法概念用配方法解一元二次方程的一般步骤：200axbxca（1）移项：将含有x的项移到方程的左边，常数项移到方程的右边；（2）二次项系数化为1：两边同除以二次项的系数；（3）配方：方程两边都加上一次项系数一半的平方；（4）将原方程变成的形式；（5）判断右边代数式的符号，若n≥0，可以直接开方求解；若n<0，原方程无解。2xmn通过配方法解一元二次方程的步骤200axbxca2xmn例1：解方程:(1)x28x+1=0﹣(2)2x2+1=3x(3)3x26x+4=0﹣解：(1)移项，得:配方，得:由此可得:±√15∴x1=4+，x2=4-x28x﹣=1﹣x28x﹣+42=1+4﹣2（x4)﹣2=15整理，得:x4=﹣探究例1：解方程:(1)x28x+1=0﹣(2)2x2+1=3x(3)3x26x+4=0﹣解：(2)移项，得:系数化为1，得:2x23x=1﹣﹣x2x﹣=-配方，得:∴x1=1，x2=x2x﹣+=-整理，得:（x)﹣2=由此可得:x﹣探究例1：解方程:(1)x28x+1=0﹣(2)2x2+1=3x(3)3x26x+4=0﹣你可以通过今天学到的方法，求出第三个方程的解吗？解：(3)移项，得:系数化为1，得:3x26x=4﹣﹣x2x﹣=-配方，得:x2﹣2x+=-整理，得:（x)﹣2=-因为实数的平方不会是负数，所以无论x取何值时，(x)﹣2都是非负数，因此方程不成立，原方程无实数根。探究一般地，如果一个一元二次方程通过配方转化成(x+n)2=p的形式，那么就有：(1)当p>0时，根据平方根的意义，方程有两个不等的实数根x1=n﹣﹣，x2=﹣n﹢；(2)当p=0时，方程有两个相等的实数根x1=x2=n﹣;pp小结pp1.在下列等式内填上适当的数,使等式成立222211224xxxx（）；（）。x-2x+6(3)x2+2x+=(x+)2;(4)x26x+﹣=(x﹣)2;(5)x2+3x+=(x+)2;(6)x2x+﹣=(x﹣)2.12132332()23274()2746222课堂测试222211224xxxx（）；（）。2.下列配方有错误的是（）22222222.41025.68031797.2760416.3420322AxxxBxxxCxxxDxxx化为化为化为化为2222222222222222.410441425.6806989317777797.2760332244416.342091260912464322AxxxxxBxxxxxCxxxxxxxDxxxxxxx，，，，，，，，，【解题过程】课堂测试22222222.41025.68031797.2760416.3420322AxxxBxxxCxxxDxxx化为化为化为化为2222222222222222.410441425.6806989317777797.2760332244416.342091260912464322AxxxxxBxxxxxCxxxxxxxDxxxxxxx，，，，，，，，，3.已知，求a，b，c的值。224xxabxc22224442xxabxcxxx。【解题过程】解：∵412abc，，。此类问题解题的关键在于通过配方法使等式两边结构相同课堂测试224xxabxc22224442xxabxcxxx。412abc，，。4.二次三项式的值（）A.小于1B.大于1C.大于等于1D.不大于12243xx【思路点拨】将二次三项式配方，然后根据平方大于等于0，求出最值。222243221213211xxxxx。【解题过程】解：∵22101x，原式。课堂测试2243xx222243221213211xxxxx。22101x，原式。感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明www.bangongziyuan.comTrendDesign老师：办公资源时间：2020.4感谢各位的仔细聆听解一元二次方程之配方法第二十一章一元二次方程PleaseEnterYourDetailedTextHere,TheContentShouldBeConciseAndClear,ConciseAndConciseDoNotNeedTooMuchText