北师大版--九年级上册--探索反比例函数基本图形面积不变性-优质课件

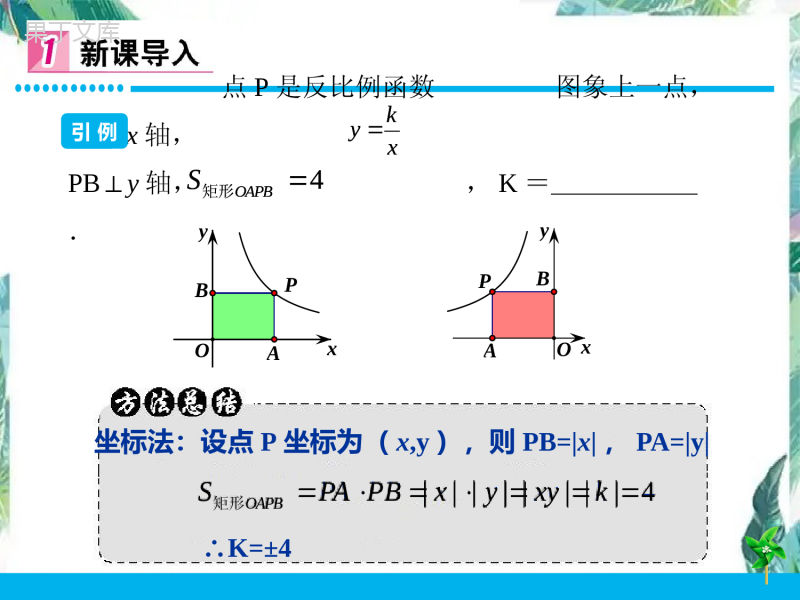
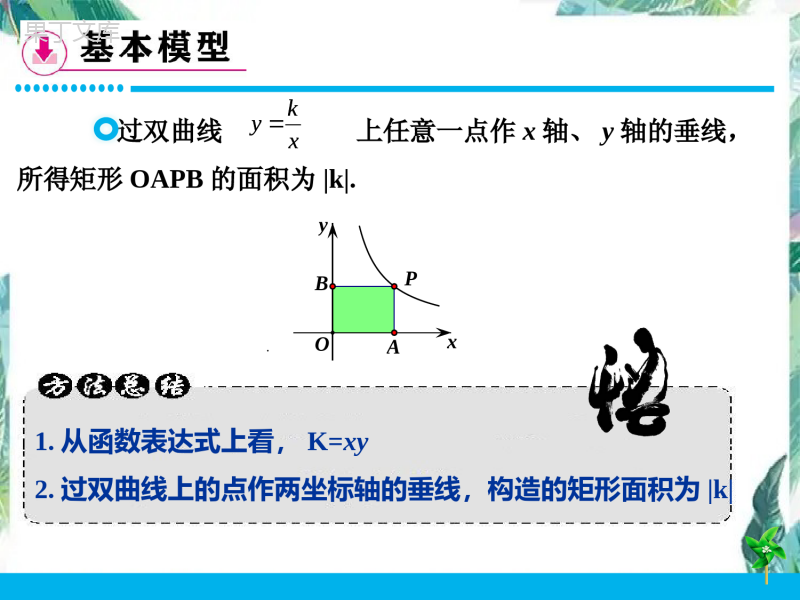
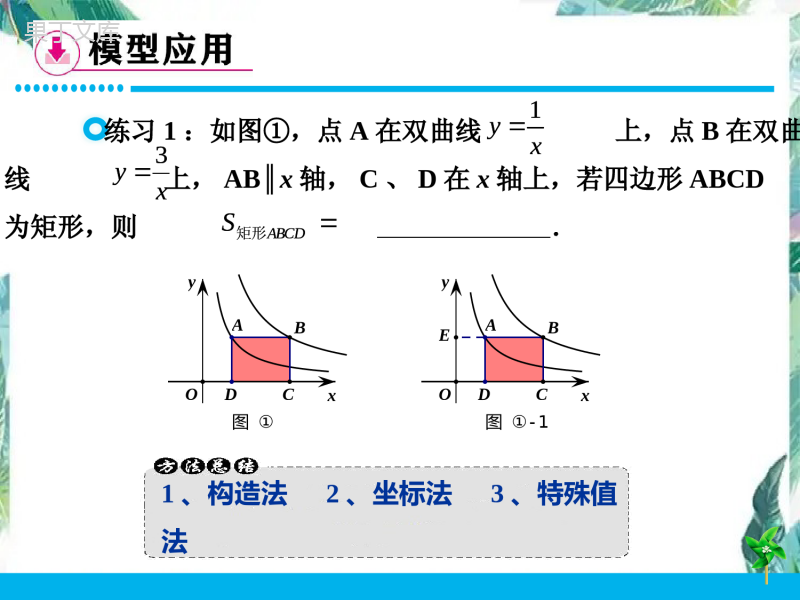
1.结合图象理解反比例函数K的几何意义2.掌握反比例函数基本图形的面积不变性3.学会从“形”与“数”两个角度思考问题4.渗透从特殊到一般、转化、数形结合思想xky4OAPBS矩形点P是反比例函数图象上一点，PA⊥x轴，PB⊥y轴，，K＝．引例xyBAOPxyxAPBO坐标法：设点P坐标为（x,y），则PB=x，PA=y∴K=±4xky4OAPBS矩形4kxyyxPBPASOAPB矩形xyBAOP．xky过双曲线上任意一点作x轴、y轴的垂线，所得矩形OAPB的面积为k.1.从函数表达式上看，K=xy2.过双曲线上的点作两坐标轴的垂线，构造的矩形面积为kxkyxy1xy3ABCDS矩形练习1：如图①，点A在双曲线上，点B在双曲线上，AB∥x轴，C、D在x轴上，若四边形ABCD为矩形，则．1、构造法2、坐标法3、特殊值法xy图①DACOBxy图①-1DAECOBxy1xy3ABCDS矩形PB边不变，让OA在x轴上移动，PACB的面积是否为定值？PA边不变，让OB在y轴上移动，PACB的面积是否为定值？xyBAOP1、分割图形：转化为两个平行四边形2、改斜归正：转化为矩形xy1xy2练习2：如图②，点A在双曲线上，点B在双曲线上，AB∥x轴，C、D在x轴上，若四边形ABCD为平行四边形，则ABCD的面积为．xy图②CBOADxy图②-1CBOADxy图②-2CBOADxy1xy22连接OP，把矩形OAPB分割成两个三角形PA边不变，点O在y轴上移动，△O´AP的面积是否为定值？△OAP、△OBP的面积分别是多少？PB边不变，点O在x轴上移动，△O´BP的面积是否为定值？xyxy2图BOAOPPxy1xy3ABCS练习3：如图③，点A在双曲线上，点B在双曲上，AB∥x轴，C在x轴上，．xy图③AOBCxy图③-1AOBCxy1xy3ABCS)0(3xxy练习4：如图④，点A是x轴正半轴上的一个定点，点P是曲线上的一个动点，PB⊥y轴于点B，当点P坐标逐渐增大时，四边形OAPB的面积将会（）逐渐增大B.不变C.逐渐变小D.先增大后减小xy图④BOPA)0(3xxy取点A关于原点的对称点A´，则.APAS取点B关于原点的对称点B´，则.BPBS取点P关于原点的对称点P´，则.PPAS取点P关于原点的对称点P´，则.PPBSxyxyxyxy2-6图2-5图2-4图2-3图BP'OP'AOB'BOA'AOPPPPAPASBPBSPPASPPBS作PDx⊥轴、PDy⊥轴，两垂线交于点D，则PPDS取点A关于原点的对称点A´，取点P关于原点的对称点P´，则.APPAS平行四边形xyxy2-8图2-7图CA'AP'AOP'OPPPPDSAPPAS平行四边形)0(xxky)0(2xxy例题如图⑤，点A、B分别在反比例函数图象上，OAOB⊥，若OB＝2OA，则K＝xy图⑤BOA)0(xxky)0(2xxy1、学会了什么数学模型？2、如何添加辅助线？3、学会了哪些解题的方法？4、感受到哪些数学思想方法？5、你还有哪些困惑？xkyAOBS如图，反比例函数图象上有两点A（2，4）（4，b），则．思考xyAOBxkyAOBS