2021-2022学年人教版初中数学七年级下册-5.1.1相交线-课件-(3)

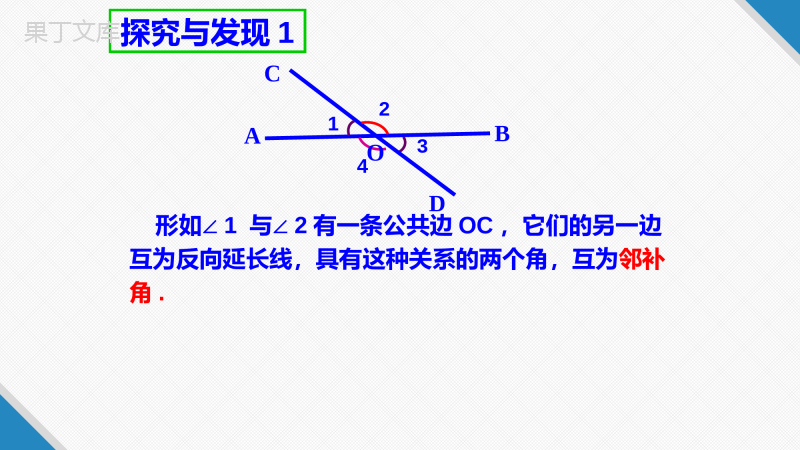
相交线和平行线是我们日常生活和生产中经常见到的，研究它们对今后的学习、工作和生活都很有用。这节课我们先来研究相交线。ABCDO直线AB、CD相交于点O如果两条直线有一个公共点，就说这两条直线相交，公共点叫做这两条直线的交点。握紧把手时，随着两个把手之间的角逐渐变小，剪刀刃之间的角也相应变小直到剪开布片。如果把剪刀的构造看作两条相交的直线，这就关系到两条相交直线所成的角的问题。观察右图，注意剪刀剪开布片过程中有关角的变化。1234ABCD形如∠1与∠2有一条公共边OC，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角.O探究与发现1OABCD）（1342）（如果两个角有一条公共边，它们的另一边互为反向延长线，那么这两个角互为邻补角。注意：(1)邻补角的本质特征是：①两个角有一条公共边；②两角的另一条边互为反向延长线。（2）邻补角是有特殊位置的两个互补的角。邻补角：图中还有哪些角也是邻补角呢？有几对邻补角？补角与邻补角有何区别和联系呢？1234ABCDO探究与发现2图中还有哪些角也是对顶角呢？形如∠1与∠3有一个公共顶点O，并且∠1的两边分别是∠3的两边的反向延长线，具有这种位置关系的两个角，互为对顶角.OABCD）（1342）（对顶角：如果两个角有一个公共点，并且其中一个角的两边是另一个角的两边的反向延长线，那么这两个角互为对顶角。注意以下两点：(1)辨认对顶角的要领：一看是不是两条直线相交所成的角，二看是不是有公共顶点；三看是不是没有公共边，(2)对顶角是成对存在的，它们是互为对顶角，如∠1是∠3的对顶角，同时，∠3是∠1的对顶角，也常说∠1和∠3是对顶角。OABCD探究与发现3对顶角相等4321∠1与∠3在数量上又有什么关系呢？对顶角的性质:对顶角相等.OABCD）（1342）（为什么?已知：直线AB与CD相交于O点(如图),求证:∠1=∠3，∠2=∠4证明：∵直线AB与CD相交于O点,∴∠1+∠2=180°，∠3+∠2=180°∴∠1=∠3同理可得：∠2=∠41练习1、下列各图中∠1、∠2是对顶角吗？为什么？21212)((())1练习2、下列各图中∠1、∠2是邻补角吗？为什么？21212)((()（∠2＝180°－∠1＝180°－30°解：由邻补角的定义，∠1=30°可得＝150°由对顶角相等，可得∠3＝∠1＝30°∠4＝∠2＝150°若∠1＋∠３=５０°，求各角的度数。若∠１=m°，求各角的度数。例题讲解例1：如图,直线a、b相交，若∠1=30°,求∠2、∠3、∠4的度数。•变式1：若∠2是∠1的3倍，求∠3的度数？•变式2：若∠2-∠1=400,求∠4的度数？？？？30°例2：如图,若∠1:∠2=3:6，求各角的度数。解:设∠1=3x°,则∠2=6x°根据邻补角的定义,得3x+6x=180x=20则∠1=60°,∠2=120°根据对顶角相等,得∠3=60°,∠4=120°答：∠1=60°,2=120°∠，∠3=30°，∠4=120°达标测试一、判断题1、有公共顶点且相等的两个角是对顶角。（）2、两条直线相交，有两组对顶角。（）3、两条直线相交所构成的四个角中有一个角是直角，那么其余的三个角也是直角。（）二、选择题1、如右图直线AB、CD交于点O，OE为射线，那么（）A、∠AOC和∠BOE是对顶角；B、∠COE和∠AOD是对顶角；C、∠BOC和∠AOD是对顶角；D、∠AOE和∠DOE是对顶角。2、如右图中直线AB、CD交于O，OE是∠BOC的平分线且∠BOE=50度，那么∠AOC=（）度ABCDOE×√√CA50°？解：∵∠DOB=∠，（）=70°（已知）∴∠DOB=°（等量代换）又∵∠1=30°（）∴∠2=∠-∠=-=°三、解答题1.如图，直线AB、CD相交于O，∠AOC=70°1=30°∠；求∠2的度数.ACBDE1AOC∠AOCDOB170°30°40对顶角相等已知702))O70°30°？2．如图，直线AB，CD，EF相交于点O，∠AOE＝40°，∠BOC＝2AOC∠，求∠DOF的度数．解：设∠AOC＝x°，则∠BOC＝(2x)°.∵∠AOC与∠BOC是邻补角，∴∠AOC＋∠BOC＝180°，则x＋2x＝180，解得x＝60，∴∠AOC＝60°.∵∠DOF与∠EOC是对顶角，∴∠DOF＝∠EOC＝∠AOC－∠AOE＝60°－40°＝20°.3．如图，直线AB，CD相交于点O，OA平分∠EOC.(1)若∠EOC＝80°，求∠BOD的度数；解：∵OA平分∠EOC，∴∠AOC＝∠EOC＝40°，从而∠BOD＝∠AOC＝40°.解：∵∠EOCEOD∠＝45∶，∴∠EOC＝80°.∵OA平分∠EOC，∴∠AOE＝40°，∴∠EOB＝180°－∠AOE＝180°－40°＝140°.(2)若∠EOCEOD∶∠＝45∶，求∠EOB的度数．归纳小结角的名称特征性质相同点不同点对顶角邻补角对顶角相等邻补角互补②有公共顶点;③没有公共边①两条直线相交形成的角；①两条直线相交而成；②有公共顶点;③有一条公共边①都是两条直线相交而成的角；③都是成对出现的②都有一个公共顶点；②两直线相交时，对顶角只有两对邻补角有四对①有无公共边