第二章相交线与平行线回顾与思考课件北师大版七年级数学下册

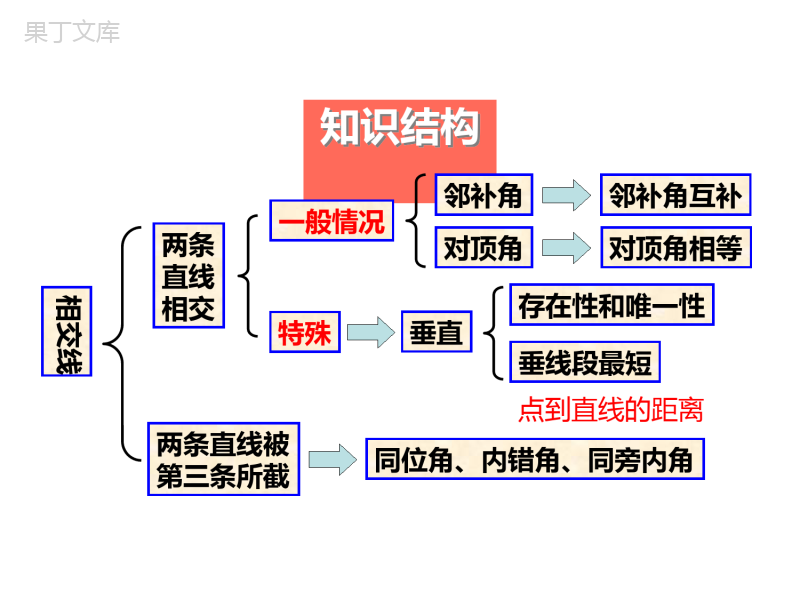
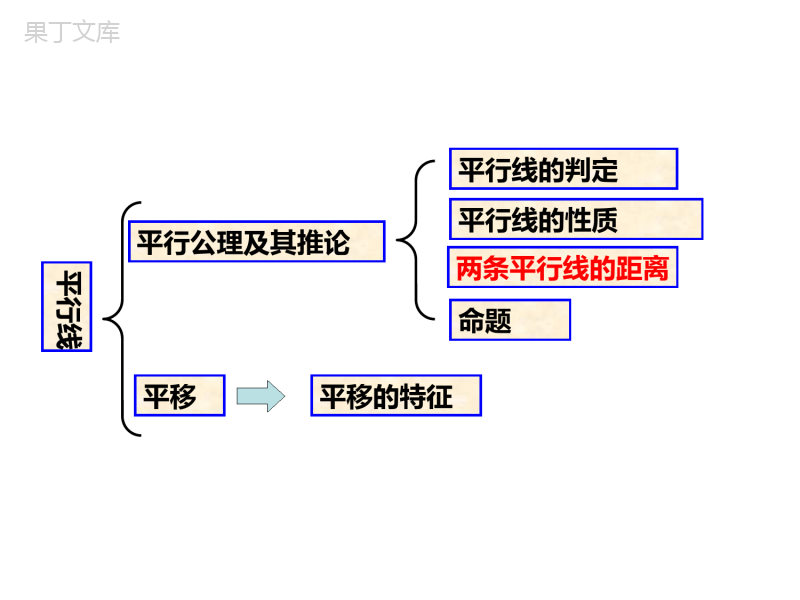
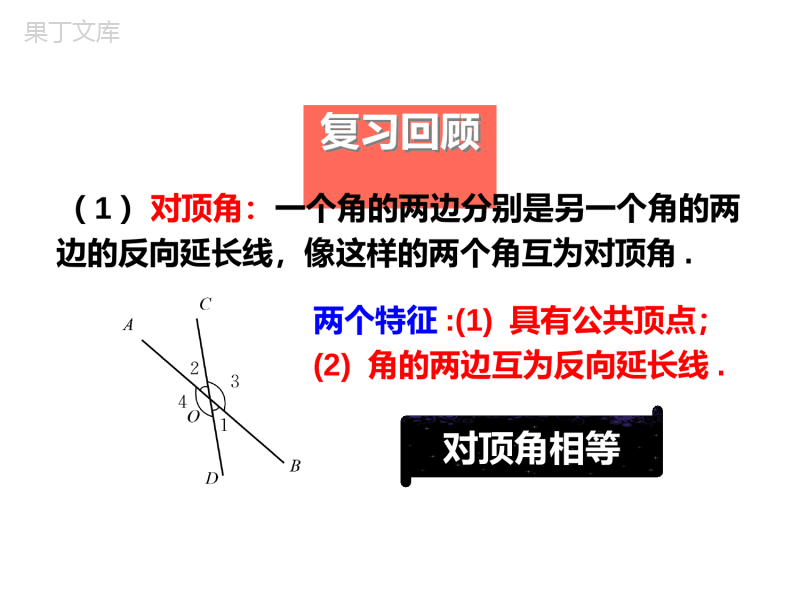
章末复习北师大版七年级数学下册知识结构相交线两条直线相交一般情况邻补角对顶角邻补角互补对顶角相等特殊垂直存在性和唯一性垂线段最短两条直线被第三条所截同位角、内错角、同旁内角点到直线的距离平行线平行公理及其推论平行线的判定平行线的性质两条平行线的距离命题平移平移的特征复习回顾（1）对顶角：一个角的两边分别是另一个角的两边的反向延长线，像这样的两个角互为对顶角.两个特征:(1)具有公共顶点；(2)角的两边互为反向延长线.对顶角相等（2）补角：如果两个角的和是180°，那么称这两个角互为补角.（3）余角：如果两个角的和是90°，那么称这两个角互为余角.（4）垂线：两条直线相交成直角时，叫做互相垂直，其中一条叫做另一条的垂线.lAlA性质1：过一点有且只有一条直线与已知直线垂直.性质2：连接直线外一点与直线上各点的所有线段中，垂线段最短.lOCBAP（5）平行线：在同一平面内，不相交的两条直线叫做平行线.bac12345678∠1与∠5像这样具有相同位置关系的一对角叫做同位角.∠4与∠6像这样的一对角叫做内错角.∠4与∠5像这样的一对角叫做同旁内角.过直线外一点有且只有一条直线与这条直线平行．平行于同一条直线的两条直线平行．ABPabcABCD4132（6）平行线的性质：性质1：两直线平行，同位角相等.性质2：两直线平行，内错角相等.性质3：两直线平行，同旁内角互补.（7）平行线的判定：判定1：同位角相等，两直线平行.判定2：内错角相等，两直线平行.判定3：同旁内角互补，两直线平行.ABCD4132（1）作射线O´A´；（2）以点O为圆心，任意长为半径作弧，交OA于点C，交OB于点D；（3）以点O´为圆心，同样(OC)长为半径作弧，交O´A´于点C´；（4）以点C´为圆心，CD长为半径作弧，交前面的弧于点D´；（5）过点D´作射线O´B´.∠A´O´B´即为所求.作法示范CDBOAC´D´如何“作一个角等于已知角”？已知：∠AOB.求作：∠A´O´B´，使∠A´O´B´=∠AOB.O´A´A´O´B´（8）用尺规作角：典例精析例1下列说法错误的是（）A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补则两直线平行典例精析例1下列说法错误的是（）A.同位角不一定相等B.内错角都相等C.同旁内角可能相等D.同旁内角互补则两直线平行B例2同一平面内，下列说法：①过两点有且只有一条直线；②两直线不平行，则一定相交；③过一点有且只有一条直线与已知直线垂直；④过一点有且仅有一条直线与已知直线平行，其中正确的个数是（）A.1个B.2个C.3个D.4个例3如图，下列条件能证明AD∥BC的是（）A.∠A=∠CB.∠B=∠DC.∠B=∠CD.∠A+∠B=180°例4如图，（1）∵∠ABD=∠BDC（已知），∴______∥（）；（2）∵∠DBC=∠ADB（已知），∴______∥（）；（3）∵∠CBE=∠DCB（已知），∴______∥（）；（4）∵∠CBE=∠A，（已知），∴______∥（）；（5）∵∠A+∠ADC=180°（已知），∴______∥（）；（6）∵∠A+∠ABC=180°（已知），∴______∥（）.例5如图，∠1=2∠，AC平分∠DAB，DC∥AB吗？为什么？例6、如图，直线abc∥∥，直角三角板的直角顶点落在直线b上，如果∠1=36°，那么∠2的度数（）。A、36°B、44°C、54°D、64°例7.如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上，如果∠1=20°，那么∠2的度数是（）。A、15°B、20°C、25°D、30°例8、如图，折叠一张矩形纸片，已知∠1=70°，则∠2的度数是（）。A、70°B、110°C、35°D、55°1.如图，AB//CD，请问：∠A、∠E、∠C满足什么关系.EDCBAEDCBAFEDCBAFEDCBAEDCBA21∠E=∠A+∠C添加辅助线单击输入您的封面副标题2.如图，AB//CD，请问：∠A、∠E、∠C满足什么关系.EDCBAEDCBAFABCDEFABCDEABCDEEDCBAABCDE∠E+∠A+∠C=360°单击输入您的封面副标题3.如图，AB//CD，请问：∠A、∠E、∠C满足什么关系.EDCBAEDCBAEDCBAF∠C=∠E+∠AG∠A=∠E+∠C单击输入您的封面副标题4.如图，AB//CD，请问：∠A、∠E、∠C满足什么关系.EDCBAEDCBAFABCDEFABCDEEDCBAABCDEABCDE∠A=∠E+∠C单击输入您的封面副标题5.如图，AB//CD，请问：∠A、∠E、∠C满足什么关系.EDCBAABCDEEDCBAABCDEABCDE∠E=180°-∠A+∠C随堂练习1.如图，BC⊥AC，CB=8cm，AC=6cm，AB=10cm，那么点A到BC的距离是______，点B到AC的距离是______，A、B两点的距离是______，点C到AB的距离是______.2.设a、b、c为平面上三条不同直线，若a//b，b//c，则a与c的位置关系是________；若a⊥b，b⊥c，则a与c的位置关系是________；若a//b，b⊥c，则a与c的位置关系是________.平行平行垂直2.设a、b、c为平面上三条不同直线，若a//b，b//c，则a与c的位置关系是________；若a⊥b，b⊥c，则a与c的位置关系是________；若a//b，b⊥c，则a与c的位置关系是________.3.下列图形中，由AB∥CD，能得到∠1=2∠的是（）4.如图，直线L1∥L2，则∠α为（）A.150°B.140°C.130°D.120°5.（1）如图，已知∠1＝∠2，试判断a、b的位置关系.（2）直线a//b，∠1=2∠吗？为什么？6.如图，已知△ABC，AD⊥BC于D，E为AB上一点，EF⊥BC于F，DG//BA交CA于G.1∠与∠2相等吗？为什么？