《变化率问题》人教版高中数学选修2-2PPT课件（第1.1.1课时）.pptx

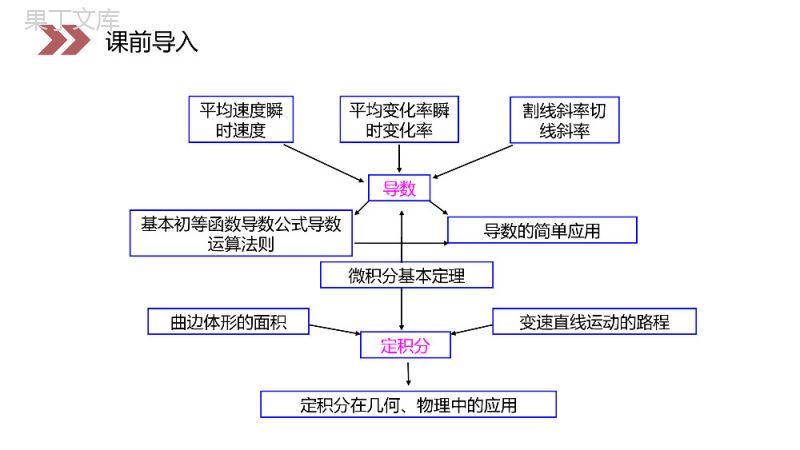
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.1.1变化率问题第1章导数及其应用人教版高中数学选修2-2为什么在相同的时间内木块的位移不一样呢？动动脑观察课前导入观察为什么跳水运动员的速度越来越快呢？课前导入课前导入解决以上2个问题,就需要我们来学习一种新的函数来解释这种现象！平均速度瞬时速度平均变化率瞬时变化率割线斜率切线斜率导数基本初等函数导数公式导数运算法则导数的简单应用微积分基本定理定积分曲边体形的面积变速直线运动的路程定积分在几何、物理中的应用课前导入问题1气球膨胀率新知探究我们都吹过气球回忆一下吹气球的过程,可以发现,随着气球内空气容量的增加,气球的半径增加越来越慢.从数学角度,如何描述这种现象呢?气球的体积V(单位:L)与半径r单位:(dm)之间的函数关系是34V(r)=πr3如果将半径r表示为体积V的函数,那么33Vr(V)=4π新知探究34V(r)=πr333Vr(V)=4π当V从0增加到1时,气球半径增加气球的平均膨胀率为r(1)-r(0)0.62(dm)r(1)-r(0)(dm/L)1-00.62当V从1增加到2时,气球半径增加气球的平均膨胀率为r(2)-r(1)0.16(dm)r(2)-r(1)(dm/L)2-10.16显然0.62>0.16新知探究r(1)-r(0)0.62(dm)r(1)-r(0)(dm/L)1-00.62r(2)-r(1)0.16(dm)r(2)-r(1)(dm/L)2-10.16思考当空气容量从V1增加到V2时,气球的平均膨胀率是多少?2121()()rVrVVV你想对了吗？新知探究2121()()rVrVVV问题2高台跳水想想运动员跳水的过程？新知探究在高台跳水运动中,运动员相对于水面的高度h(单位：米)与起跳后的时间t（单位：秒）存在函数关系h(t)=-4.9t2+6.5t+10.如何用运动员在某些时间段内的平均速度粗略地描述其运动状态?请计算0t0.5≦≦和1t2≦≦时的平均速度在0t0.5≦≦这段时间里h(0.5)-h(0)v==4.05m/s)0.5-0（在1t2≦≦这段时间里h(2)-h(1)v==-8.2m/s)2-1（新知探究h(0.5)-h(0)v==4.05m/s)0.5-0（h(2)-h(1)v==-8.2m/s)2-1（探究计算运动员在这段时间里的平均速度，并思考下面的问题：650t49（1）运动员在这段时间里是静止的吗？（2）你认为用平均速度描述运动员运动状态有什么问题？新知探究650t49平均速度不能反映他在这段时间里运动状态，需要用瞬时速度描述运动状态.新知探究同学们，从上面的问题中能够发现什么共同点呢？总结2121f(x)-f(x)x-x新知探究以上两个问题都是求变化率，我们可以用函数关系式y=f(x)来表示.那么变化率为2121f(x)-f(x)x-x上述问题中的变化率可用式子表示称为函数f(x)从x1到x2的平均变化率.2121f(x)-f(x)x-x很重要！知识要点新知探究2121f(x)-f(x)x-x一般我们用Δx表示，即.21x-x21Δx=x-x21类似地,Δf=fx-fx..于是,平均变化率可示为ΔfΔx表新知探究21x-x21Δx=x-x21类似地,Δf=fx-fx..于是,平均变化率可示为ΔfΔx表是一个整体符号，而不是与相乘.注意！x很重要！新知探究xxx例题11、已知函数f(x)=-x2的图象上的一点A(-1,-1)及临近一点B(0,0),则Δy/Δx=()A.3B.4C.1D.-1c新知探究解：=0-(-1)=1；=0-（-1）=1；yx1yxyx1yx•观察函数f(x)的图象平均变化率表示什么?2121f(x)-f(x)x-xOABxyY=f(x)x1x2f(x1)f(x2)X2-x1f(x2)-f(x1)直线AB的斜率例题2新知探究2121f(x)-f(x)x-x汽车在前两秒内速度由0增加到10m/s,在后两秒内增至30m/s,其运动状态如何呢？如果我们用平均速度描述其运动状态，前两秒内:v=5(m/s)后两秒内：v=10(m/s)你想对了吗？例题3新知探究想一想你还能想到生活中类似的问题吗？举个例子吧！新知探究我们把式子称为函数f(x)从到的平均变化率.（averagerateofchange）2121fx-fxx-x1x2x课堂小结平均变化率的求解步骤：（1）求函数的增量Δf=Δy=f(x2)-f(x1);（2）计算平均变化率fx.2121f(x)-f(x)x-x2121fx-fxx-x1x2xfx.2121f(x)-f(x)x-x1、已知函数f(x)=-x2+x的图象上的一点A（-1,-2）及临近一点B（-1+Δx,-2+Δy），则Δy/Δx=（）A.3B.3Δx-(Δx)2C.3-(Δx)2D.3-ΔxD课堂练习2、函数在区间上的平均变化率是（）2fx=x-1,3A.4B.21434C.D.B2Δy3-1解：==2Δx3-(-1)课堂练习2fx=x-1,314342Δy3-1解：==2Δx3-(-1)3、函数在区间[1，1.5]上的平均变化率为_______________.2y=2x222-1.15.1.5-1yx得（1.5）5解：由平均变化率的公式课堂练习2y=2x222-1.15.1.5-1yx得（1.5）4、已知函数,则变化率可用式子_____________，此式称之为函数从到的___________.平均变化率可以表示为_____________.fx2121fx-fxx-x1x2x平均变化率ΔyΔx你做对了吗？课堂练习fx2121fx-fxx-x1x2xΔyΔx5、过曲线y=f(x)=x3上两点P（1，1）和Q（1+Δx,1+Δy）作曲线的割线，求出当Δx=0.1时割线的斜率.解：K=3Δx+(Δx)2=3+3×0.1+(0.1)2=3.31.课堂练习6、已知一次函数在区间[-2，6]上的平均变化率为2，且函数图象过点（0，2），试求此一次函数的表达式.y=f(x)课堂练习解：由平均变化率的含义可知该直线的斜率为2，设直线方程为y=2x+b,又因为直线经过点（0，2），代入方程得b=2.则直线方程为：y=2x+2.y=f(x)感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2