2021-2022学年人教版数学九年级上册24.4.1弧长及扇形面积--课件

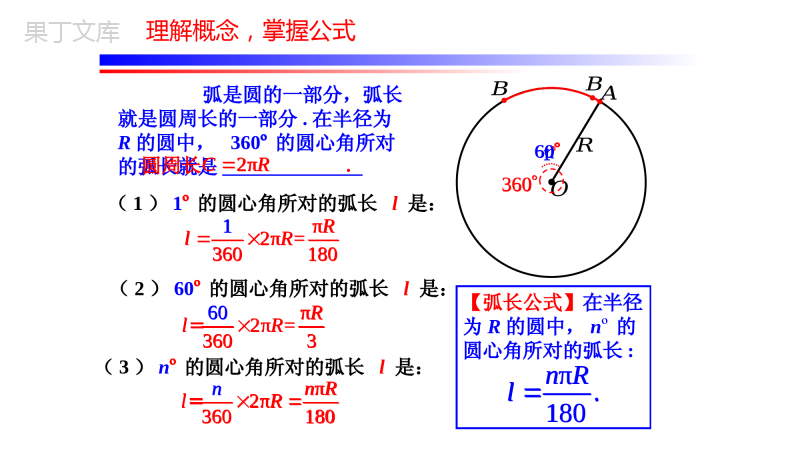
学习目标1了解扇形的概念；2理解并掌握弧长和扇形面积的计算公式；3会利用弧长和扇形面积公式熟练计算。【思考】如图，若这个圆的直径为4米，A，B两点分别表示其中两条轴的端点.可以发现，这个大水车的外圈是一个以O为圆心，OA为半径的圆，6条轴（直径）把这个圆平均分成了12等分.（2）如何求与半径OA、OB所围成图形的面积呢？??⏜（1）如何求的长度呢？??⏜我们身边的数学2πCR2πSR2πCR2πSR（1）1º的圆心角所对的弧长l是：（3）nº的圆心角所对的弧长l是：弧是圆的一部分，弧长就是圆周长的一部分.在半径为R的圆中，360º的圆心角所对的弧长就是______________π2π1=360180RlR（2）60º的圆心角所对的弧长l是：π2π=360630RlR=π2π360180nRlRn=π.180nRl【弧长公式】在半径为R的圆中，nº的圆心角所对的弧长:2πCR圆周长.?????160n360理解概念，掌握公式π2π1=360180RlRπ2π=360630RlR=π2π360180nRlRn=π.180nRl2πCR160n360【练习1】如图，等边△ABC的边长为1．依次以A，B，C为圆心，以AC，BC1，CC2为半径画弧（其中C1，C2，C3分别在边BA，CB，AC的延长线上）．试计算曲线C-C1-C2-C3的“展直长度”L.120π1120π2120π3=++180180180L解：246=π+π+π=4π333课堂小练，巩固提高120π1120π2120π3=++180180180L解：246=π+π+π=4π333【思考】图中阴影部分面积总和是_______平方单位？14π32π360nRS扇形S扇形120由组成圆心角的两条半径和圆心角所对的弧围成的图形叫做扇形.nR232120π33π360CCCS扇形12120π11π3603ACCS扇形122120π24π3603BCCS扇形π180nRl在半径为R的圆中，圆的面积是，2πSR那么圆心角为nº的扇形面积是：3R12lR类比弧长公式，推导扇形面积公式14π32π360nRS扇形S扇形120nR232120π33π360CCCS扇形12120π11π3603ACCS扇形122120π24π3603BCCS扇形π180nRl2πSR3R12lR如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m.求截面上有水部分的面积(结果保留小数点后两位).,,OAOB解：如图所示,连接,ODABABC作交于点,ACAOOCAOC△是等边三角形0.6m,0.60.30.3(m),OAODOABOABSSS扇形有水部分的面积：60,120.AODAOB,,ODCDADOC即垂直平分22120π0.610.630.30.22(m)3602SDC由弦及其所对的弧组成的图形叫做弓形.??.AC连接220.60.30.33,0.63,ADAB细心观察，认真思考,,OAOB解：如图所示,连接,ODABABC作交于点,ACAOOCAOC△是等边三角形0.6m,0.60.30.3(m),OAODOABOABSSS扇形有水部分的面积：60,120.AODAOB,,ODCDADOC即垂直平分22120π0.610.630.30.22(m)3602SDC.AC连接220.60.30.33,0.63,ADAB【变式】水平放置的圆柱形排水管道的截面半径是0.6m,其中水面宽m.那么截面上有水部分的面积为____________m2(结果保留小数点后两位).0.63如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m.求截面上有水部分的面积(结果保留小数点后两位).0.22SSS圆原弓形+SSS三角形扇形或SSS三角形扇形SSS弓形三角形扇形0.91或DC???细心观察，认真思考20.6π0.220.91S割补法0.630.22SSS圆原弓形+SSS三角形扇形或SSS三角形扇形SSS弓形三角形扇形0.91或DC20.6π0.220.91S【练习2】如图，正三角形ABC的边长为a，D，E，F分别为BC，CA，AB的中点，以A，B，C三点为圆心，长为半径作圆.求图中阴影部分的面积.?23ABCAFESSS阴影扇形260π()132322180aaa223π8a换成字母也一样3ABCAFESSS阴影扇形260π()132322180aaa223π8a【思考】如图，若这个圆的直径为4米，A，B两点分别表示其中两条轴的端点.可以发现，这个大水车的外圈是一个以O为圆心，OA为半径的圆，6条轴（直径）把这个圆平均分成了12等分.（2）如何求与半径OA、OB所围成图形的面积呢？??⏜（1）如何求的长度呢？??⏜60π22π(m)1803lAB2260π22π(m)3603OABS扇形回归课题，解决问题60π22π(m)1803lAB2260π22π(m)3603OABS扇形【数学日记】学习是一个知识积累的过程，在这个过程中，我们应当注意前后知识的联系、转化与类比等，这样，认识才能不断深化，能力才能不断提高.2π360nRS扇形12SlR扇形或π180nRl回顾本节课知识，思考并回答下列问题：（1）弧长和扇形面积公式是什么？（2）你是如何推导得到这两个公式的？通过知识之间的转化、类比来获得新知识.SSS弓形三角形扇形比如：（3）通常可以采用什么方法求不规则图形的面积？割补法善于总结是一个良好的学习习惯2π360nRS扇形12SlR扇形或π180nRlSSS弓形三角形扇形比如：课堂练习1.75°的圆心角所对的弧长是2.5πcm，则此弧所在圆的半径是cm。62.半径为6的圆中，30°圆周角所对的弧长是cm。2π4.一个扇形的弧长为20πcm，面积是240πcm2，则扇形的半径。3.一个扇形的圆心角为120°,它的面积为3πcm2，那么该扇形的半径.3cm圆心角24cm150°课堂练习5、已知扇形的圆心角为120°，半径为2，则这个扇形的面积，S扇=_.346、已知半径为2的扇形，其弧长为，则这个扇形的面积，S扇=——．3434如图，继续依次以A，B，C……为圆心，AC3，BC4，CC5……为半径画弧……，试探究曲线C-C1-C2…-Cn的“展直长度”为：_________（用含n的代数式表示）.课后探究，提升思维运用新知提升能力ABCA'C'B'A"L1.把Rt△ABC的斜边放在直线L上,绕点B按顺时针方向在L上转两次,使它转到A"B'C',设BC=1，∠CAB=30°,则顶点A运动到点A"的位置时，（1）点A所经过的路线长是多少？运用新知提升能力1.把Rt△ABC的斜边放在直线L上,绕点B按顺时针方向在L上转两次,使它转到A"B'C',设BC=1，∠CAB=30°,则顶点A运动到点A"的位置时，（1）点A所经过的路线长是多少？（2）点A所经过的路线长与L所围成的面积？ABCA'C'B'A"L2.如图，已知菱形ABCD的边长为1.5，B，C两点在扇形AEF的弧EF上，求：及扇形ABC的面积.⌒BC运用新知提升能力祝：同学们学习进步!同仁们工作顺利!