《椭圆及其标准方程》人教版高二数学选修2-1PPT课件（第1课时）.pptx

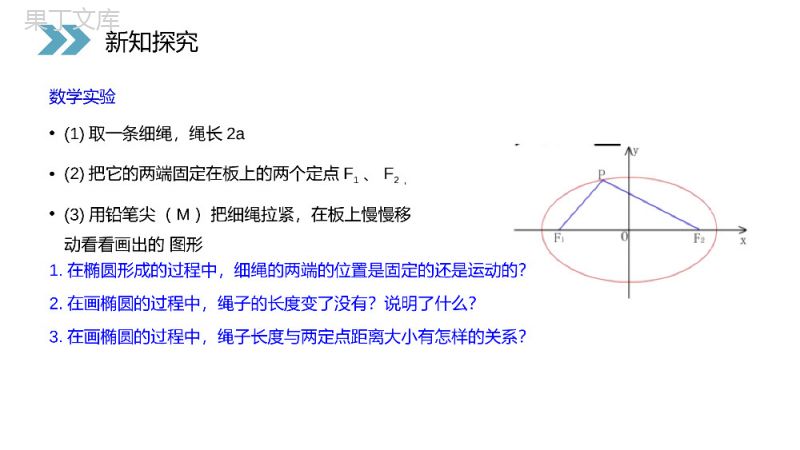
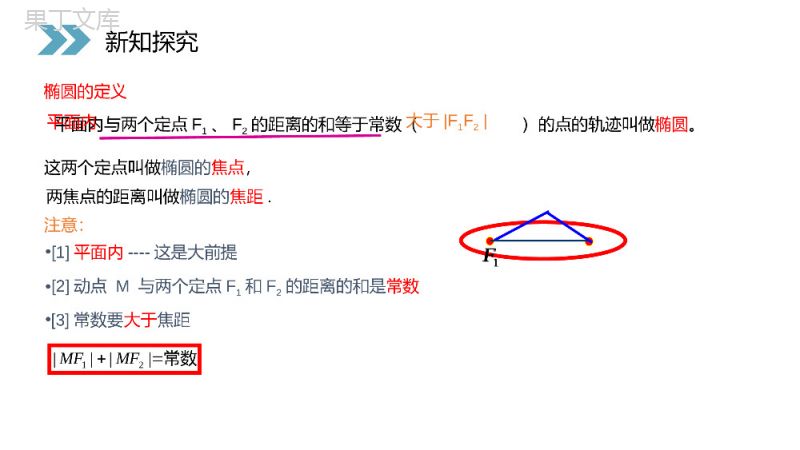
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-12.2.1椭圆及其标准方程第一课时第2章圆锥曲线与方程人教版高中数学选修2-1FEDEDFEyDxyxrbarbyaxyx421,2,2,04,,)()(3)2()(y)(xAB12222222212212半径为）圆心（）圆的一般方程：（），半径为圆心为（）圆的标准方程：（的点的轨迹的集合到定点的距离等于定长圆的定义：）两点间的距离公式：（复习检测FEDEDFEyDxyxrbarbyaxyx421,2,2,04,,)()(3)2()(y)(xAB12222222212212半径为）圆心（）圆的一般方程：（），半径为圆心为（）圆的标准方程：（的点的轨迹的集合到定点的距离等于定长圆的定义：）两点间的距离公式：（问题1：取一条定长的细绳，把它的两端都固定在图板的同一点处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖（动点）画出的轨迹是一个什么图形？笔尖（动点）满足什么几何条件？问题一：椭圆的画法新知探究数学实验•(1)取一条细绳，绳长2a•(2)把它的两端固定在板上的两个定点F1、F2，•(3)用铅笔尖（M）把细绳拉紧，在板上慢慢移动看看画出的图形1.在椭圆形成的过程中，细绳的两端的位置是固定的还是运动的？2.在画椭圆的过程中，绳子的长度变了没有？说明了什么？3.在画椭圆的过程中，绳子长度与两定点距离大小有怎样的关系？新知探究平面内与两个定点F1、F2的距离的和等于常数（）的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距.注意：•[3]常数要大于焦距1F•[2]动点M与两个定点F1和F2的距离的和是常数椭圆的定义•[1]平面内----这是大前提平面内大于F1F2常数21MFMF新知探究1FMF1F2时，动点的轨迹为）当（FFMFMF12121时，动点的轨迹为）当（FFMFMF22121时，动点的轨迹为）当（FFMFMF32121问题2:当点M到F1、F2的距离之和不大F1F2时，点M的轨迹是什么？1FM2F椭圆线段F1F2不存在新知探究时，动点的轨迹为）当（FFMFMF12121时，动点的轨迹为）当（FFMFMF22121时，动点的轨迹为）当（FFMFMF321211FM2F例1：用定义判断下列动点M的轨迹是否为椭圆.(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹.(2)到F1(0,-2)、F2(0,2)的距离之和为4的点的轨迹.(3)到F1(-2,0)、F2(0，2)的距离之和为3的点的轨迹.是不是是新知探究问题1：根据椭圆的形状，如何建立直角坐标系？建立平面直角坐标系通常遵循的原则：对称、“简洁”OxyOxyOxyMF1F2方案一F1F2方案二OxyMOxy问题二：椭圆方程的推导新知探究解：取过焦点F1、F2的直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系(如图).设M(x,y)是椭圆上任意一点，椭圆的焦距2c(c>0)，M与F1和F2的距离的和等于正常数2a(2a>2c)，则F1、F2的坐标分别是(-c,0)、(c,0).xF1F2M0y含有两个根号的式子，怎样化简呢？aMFMF221222221)(,)(ycxMFycxMFaycxycx2)()(2222得方程由椭圆的定义得:根据两点间距离公式建系设点列式化简问题2：如何求椭圆的方程呢？新知探究aMFMF221222221)(,)(ycxMFycxMFaycxycx2)()(2222得方程)(222caa两边除以得.122222cayax2222222222422yacacxaxaxccxaa两边再平方，得整理得)()(22222222caayaxca移项2222)(2)(ycxaycx2222222)()(44)(ycxycxaaycx平方222)(ycxacxa整理得新知探究)(222caa.122222cayax2222222222422yacacxaxaxccxaa)()(22222222caayaxca2222)(2)(ycxaycx2222222)()(44)(ycxycxaaycx222)(ycxacxa642-2-4-6-8-10-5510F1BF2xyOMMMabc222cab0ba的线段吗？代表找出观察椭圆，你能从图中22,,caca问题3：a—长半轴长b—短半轴长c—半焦距长轴长：2a短轴长：2b焦距：2c新知探究222cab0ba的线段吗？代表找出观察椭圆，你能从图中22,,caca令,222bca其中0b代入上式，得)0(12222babyax焦点是F1(-c,0)、F2(c,0)该方程叫做椭圆的标准方程。这里，222bac椭圆的标准方程F1F2MOxy新知探究,222bca0b)0(12222babyax222bacF1F2MOxyF1F2MOxy)0(12222babxay问题4：如果焦点在y轴上，椭圆的标准方程会是什么？x2与y2的分母哪一个大，则焦点在哪一个轴上.当焦点在y轴上时，焦点是F1(0，-c)、F2(0，c)新知探究)0(12222babxay22(2)12516xy2222(5)11xymm22(1)11616xy22(3)9252250xy22(4)321xy例2：下列方程哪些表示椭圆？若表示椭圆焦点在那个轴上？（m不为0）变式：p36页练习第1,2题（P42页）课堂练习22(2)12516xy2222(5)11xymm22(1)11616xy22(3)9252250xy22(4)321xy目标检测：(1)已知椭圆的方程为：,则a=_____，b=_______，c=_______，焦点坐标为：，焦距等于_____;若曲线上一点M到左焦点F1的距离为3，则点M到另一个焦点F2的距离等于_________，则∆F1MF2的周长为___________15422yx21(0,-1)、(0,1)25253252MF1+MF2=2aF1F2MOxyF1F2MOxy课堂练习15422yx5253252(2)已知椭圆的方程为：，则a=_____，b=_______，c=_______，焦点坐标为：____________焦距等于______;若CD为过左焦点F1的弦，则∆F2CD的周长为________1162522yx543(3,0)、(-3,0)6２0CF1+CF2=2a（3）a=5，c=4的椭圆标准方程是192522yx192522xy或F1F2CD课堂练习1162522yx192522yx192522xy1、椭圆的定义：我们把平面内与两个定点的距离之和等于常数的点的轨迹叫做椭圆。21,FF（大于）21FF（a>c）即2a21MFMF2、椭圆的图形与标准方程这两个定点F1,F2叫做椭圆的焦点，两焦点间的距离F1F2叫做焦距。课堂小结21,FF21FF21MFMF2222+=1>>0xyabab标准方程中，分母哪个大，焦点就在哪个轴上!12-,0,0，FcFc120,-0,，FcFc标准方程相同点焦点位置的判断不同点图形焦点坐标a、b、c的关系焦点在x轴上焦点在y轴上222cab22221(0)yxababyxMOF1F2课堂小结2222+=1>>0xyabab12-,0,0，FcFc120,-0,，FcFc222cab22221(0)yxabab感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第2章圆锥曲线与方程人教版高中数学选修2-1