2022年秋鲁教版(五四制)数学九年级上册---三角函数的应用-课件

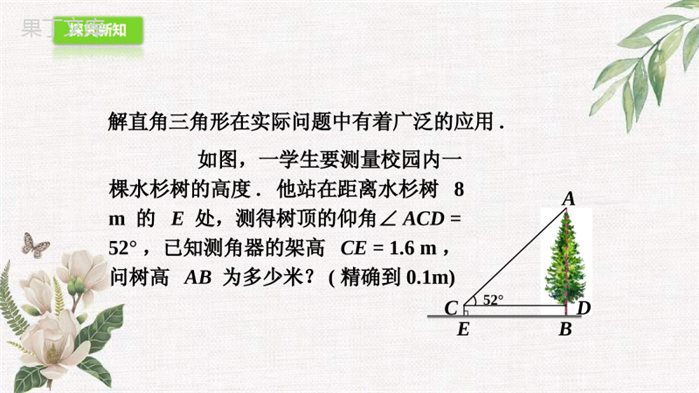
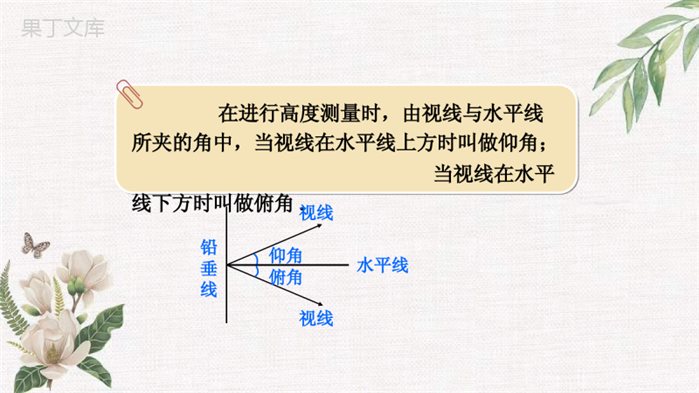
2.5三角函数的应用1.巩固用三角函数有关知识解决问题,学会解决坡度、坡角问题.2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.3.培养学生的数学意识,渗透数形结合的数学思想和方法.重点:理解坡度和坡角的概念.难点:利用坡度和坡角等条件,解决有关的实际问题.对于坡度i表示成1∶m的形式学生易疏忽,教学中应着重强调,引起学生的重视.解直角三角形在实际问题中有着广泛的应用.如图，一学生要测量校园内一棵水杉树的高度.他站在距离水杉树8m的E处，测得树顶的仰角∠ACD=52°，已知测角器的架高CE=1.6m，问树高AB为多少米？(精确到0.1m)EBDCA52°在进行高度测量时，由视线与水平线所夹的角中，当视线在水平线上方时叫做仰角；当视线在水平线下方时叫做俯角.铅垂线水平线仰角俯角视线视线EBDCA52°解在Rt△ACD中，∠ACD=52°，CD=EB=8m.由tan∠ACD=，得ADCDAD=CD·tan∠ACD=8×tan52°=8×1.2799≈10.2（m）EBDCA52°由DB=CE=1.6m，得AB=AD+DB=10.2+1.6=11.8（m）答：树高AB为11.8m.例例11如图，铁路路基的横断面是四边形ABCD.AD∥BC，路基顶宽BC=9.8m，路基高BE=5.8m，斜坡AB的坡度i=1:1.6，斜坡CD的坡度i′=1:2.5，求铁路路基下底宽AD的值（精确到0.1m）与斜坡的坡角α和β(精确到1°)的值.ADEBCαβi=1∶1.6i′=1∶2.59.8ADEBCαβi=1∶1.6i′=1∶2.59.8解过点C作CF⊥AD于点F，得CF=BE，EF=BC，∠A=α，∠D=β.F∵BE=5.8m，，，BEAE11.6CFDF12.5ADEBCαβi=1∶1.6i′=1∶2.59.8F∴AE=1.6×5.8=9.28（m），DF=2.5×5.8=14.5（m）.AD=AE+EF+DF=9.28+9.8+14.5≈33.6（m）ADEBCαβi=1∶1.6i′=1∶2.59.8F由tanα=i=，tanβ=i′=，得11.612.5α≈32°，β≈22°.答：铁路路基下底宽为33.6m，斜坡的坡角分别为32°和22°例例22已知：在直线y=kx+b上有任意两点P1（x1，y1），P2（x2，y2），这条直线向上方向与x轴正方向所夹的锐角为α.求证：tanα==k.yyxx2121证明证明由α是锐角，可知直线y=kx+b是上升的，即函数y=kx+b的值随x值的增大而增大.xyOαQ1Q2αRP1（x1，y1）P2（x2，y2）如图，设x1＜x2，则y1＜y2.过点P1，P2作x轴的垂线，垂足分别为Q1，Q2，再过点P1作x轴的平行线P1R交P2Q2于点R，得∠P2P1R=α.xyOαQ1Q2αRP1（x1，y1）P2（x2，y2）∵P1，P2都在直线y=kx+b上，∴y1=kx1+b，①y2=kx2+b.②由②–①，得在△P2P1R中，tanα===RPRP21yyxx2121yyxx2121xyOαQ1Q2αRP1（x1，y1）P2（x2，y2）y2–y1=k（x2–x1）∴k=.yyxx2121即tanα==k.yyxx2121谈谈你的收获