第7章--锐角三角函数-复习课件

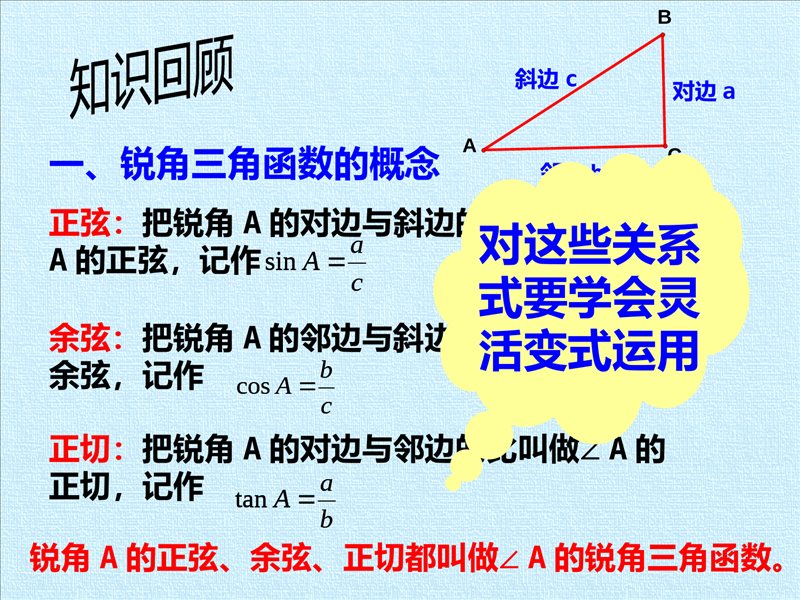
第7章锐角三角函数复习课件学习目标知识回顾典型例题和及时反馈1.巩固三角函数的概念，巩固用直角三角形边之比来表示某个锐角的三角函数。2.熟记30°，45°，60°角的三角函数值。会计算含有特殊角的三角函数的值，会由一个特殊锐角的三角函数值，求出它的对应的角度。3.掌握直角三角形的边角关系，会运用勾股定理，直角三角形的两锐角互余及锐角三角函数解直角三角形。4.会用解直角三角形的有关知识解决简单的实际问题。锐角三角函数1.锐角三角函数的定义⑴正弦⑵余弦⑶正切2.30°、45°、60°特殊角的三角函数值3.解直角三角形⑴定义⑵解直角三角形的依据①三边间关系②锐角间关系③边角间关系⑶解直角三角形在实际问题中的应用一、锐角三角函数的概念正弦：把锐角A的对边与斜边的比叫做∠A的正弦，记作caAsin余弦：把锐角A的邻边与斜边的比叫做∠A的余弦，记作正切：把锐角A的对边与邻边的比叫做∠A的正切，记作cbAcosbaAtanBCA对边a邻边b斜边c锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。对这些关系式要学会灵活变式运用caAsincbAcosbaAtan同一锐角的正弦值和余弦值之间的关系是：正弦值等于它的余角的余弦值，余弦值等于它的余角的正弦值。sinA＝cos（90°一A）＝cosBcosA＝sin（90°一A）＝sinB思考：同一个锐角的正弦值和余弦值之间有何关系？二、特殊角的三角函数值2123222123223313锐角的三角函数值有何变化规律呢？2123222123223313三、解直角三角形由直角三角形中，除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形。1.什么叫解直角三角形？2.直角三角形中的边角关系：222cba∠A十∠B＝90°caAsincbAcosbaAtan归纳：只要知道其中的2个元素（至少有一个是边），就可以求出其余3个未知元素。（1）三边关系：（勾股定理）（2）两锐角的关系：（3）边角的关系：222cbacaAsincbAcosbaAtan四、解直角三角形的应用1.仰角和俯角在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角。铅直线水平线视线视线仰角俯角坡度（坡比）：坡面的铅直高度h和水平距离l的比叫做坡度，用字母i表示，则2.坡度、坡角坡角：坡面与水平面的夹角叫做坡角，用字母α表示。tanhilhltanhil坡度通常写成的形式。tanhiltanhil解：原式=2×+1×2121=1+21例1.计算2sin30°+tan45°×cos60°21=步骤：一“代”二“算”例2.若，则锐角α=01tan330°点拨：本题是由特殊角的三角函数值求角度，首先将原式变形为tanα=，从而求得α的度数。332121212101tan333例3.在Rt△ABC中，∠C=90°，∠A=30°，a=5，求b、c的大小。解:∵sinA=a/c，∴c=a/sinA=5/sin30=5/(1/2)=10。ABC530°∠B=90°-∠A=90°-30°=60°，∵tanB=b/a，∴b=a·tanB=5·tan60°=35解直角三角形分为两类:一是已知一边一角解直角三角形；二是已知两边解直角三角形。35例4.如图，在△ABC中，AD是BC边上的高，若tanB=cos∠DAC。（１）AC与BD相等吗？说明理由；DCBA故BD=AC解：（１）在Rt△ABD和△ACD中，tanB=，＝BDADACAD因为tanB=cos∠DAC，所以＝BDADACADcos∠DAC（２）若sinC＝，BC=12，求AD的长。1312BDADACADBDADACAD1312例4.如图，在△ABC中，AD是BC边上的高，若tanB=cos∠DAC。（１）AC与BD相等吗？说明理由；DCBA（２）若sinC＝，BC=12，求AD的长。1312设AC=13k，AD=12k，所以CD=5k，又AC=BD=13k，（2）在Rt△ACD中，因为sinC＝1312所以BC=18k=12，故k=32所以AD=12×＝８32131213123232.30cos260tan45sin22)1(200026tan303sin602cos45.1.若，则锐角α=02sin22.若，则锐角α=0320tan(）3.计算：45°80°21221.30cos260tan45sin22)1(200026tan303sin602cos45.02sin20320tan(）212214.如图，在Rt△ABC中，∠C=90，b=，c=4。则a=，∠B=，∠A=。32ABC260°30°D5.如果那么△ABC是（）A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形03tan321cosBA3203tan321cosBA例5.海中有一个小岛P，它的周围18海里内有暗礁，渔船跟踪鱼群由西向东航行，在点A测得小岛P在北偏东60°方向上，航行12海里到达B点，这时测得小岛P在北偏东45°方向上。如果渔船不改变航线继续向东航行，有没有触礁危险？请说明理由。D分析：作PD⊥BC，设PD=x，则BD=x，AD=x+12，根据AD=PD，得x+12=x，求出x的值，再比较PD与18的大小关系。3333解：有触礁危险。理由：过点P作PD⊥AC于D。设PD为x，在Rt△PBD中，∠PBD=90°－45°＝45°。∴BD＝PD＝x，AD=12+x。在Rt△PAD中，∵∠PAD＝90°－60°＝30°，,3PDAD∴渔船不改变航线继续向东航行，有触礁危险。,312xx18)13(61312xD,3PDAD,312xx18)13(61312x例6.我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示，BCAD∥，斜坡AB=40米，坡角∠BAD=60°，为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造。经地质人员勘测，当坡角不超过45°时，可确保山体不滑坡，改造时保持坡脚A不动，从坡顶B沿BC削进到E处，问BE至少是多少米（结果保留根号）？GF分析:就是当∠EAD=45°时，求BE的长，作BF⊥AD，EG⊥AD，则BE=GF=AG-AF。过点B作BF⊥AD，在Rt△ABF中，AB=40，∠BAD=60°，过点E作EG⊥AD，在Rt△ABF中，GE=BF当∠EAD=45°时，,320sinBADABBF。20cosBADABAF,320GEAG20320AFAGGFBE点评：题目中没有直角三角形时，我们可以作辅助线构造直角三角形，作辅助线时要考虑如何充分和便利的使用已知条件。GF解:,320sinBADABBF。20cosBADABAF,320GEAG20320AFAGGFBE6.直角三角形纸片的两直角边分别BC为6，AC为8，现将△ABC，按如图折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是。ABC68ED方法点拨:设CE=x，则AE=BE=8-x，利用勾股定理求出x，再求tan∠CBE的值。2472477.如图，某数学兴趣小组在活动课上测量学校旗杆高度。已知小明的眼睛与地面的距离是1.7m，看旗杆顶部的仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，看旗杆顶部的仰角为30°。两人相距28米且位于旗杆两侧（点B，N，D在同一条直线上）。请求出旗杆MN的高度。（结果保留整数）MN=12米8.如图，甲船在港口P的北偏西60°方向，距港口80海里的A处，沿AP方向以12海里/时的速度驶向港口P。乙船从港口P出发，沿北偏东45°方向匀速驶离港口P，现两船同时出发，2小时后乙船在甲船的正东方向，求乙船的航行速度。214214谢谢