第4课时-一次函数的应用(课件)-2022-2023学年八年级数学上册同步精品课堂(北师大版)

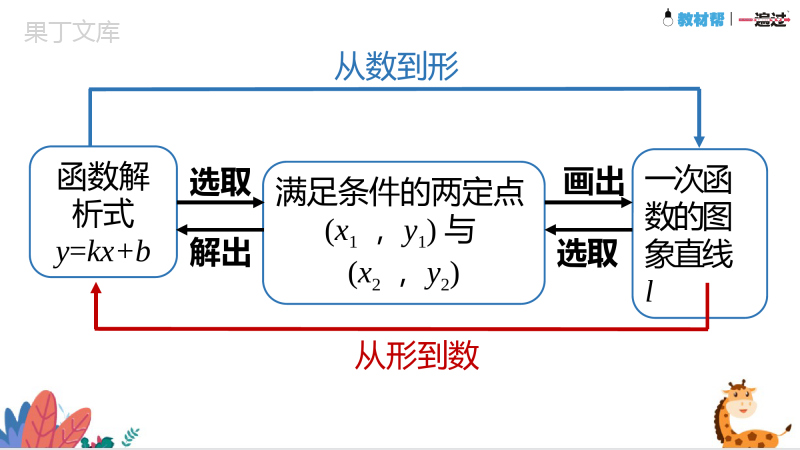
第4课时一次函数的应用例4已知一次函数的图象经过点(3，5)与(-4，-9)，求这个一次函数的解析式.知识点：待定系数法求一次函数解析式新知探究分析：求一次函数y=kx+b的解析式，关键是求出k，b的值.从已知条件可以列出关于k，b的二元一次方程组，并求出k，b.这两点的坐标适合解析式解：设这个一次函数的解析式为y=kx+b（k≠0）∵y=kx+b的图象过点（3，5）与（-4，-9）,3k+b=5,-4k+b=-9,∴∴这个一次函数的解析式为y=2x-1.k=2,b=-1,解得待定系数法：先设出函数解析式，再根据条件确定解析式中未知的系数，从而得出函数解析式的方法，叫做待定系数法.由上面的例题你能归纳出求函数解析式的方法吗？函数解析式y=kx+b满足条件的两定点(x1，y1)与(x2，y2)一次函数的图象直线l选取解出选取画出从数到形从形到数设出一次函数的解析式y=kx+b（k≠0）解所列的方程组，求出k，b的值列设解将已知的两组x，y的对应值分别代入所设的解析式中，列出关于k，b的二元一次方程组用待定系数法求一次函数解析式的步骤将求出的k，b的值代入所设解析式中，得到所求一次函数的解析式代一次函数应用的两种类型：（1）题目中已知一次函数的解析式，可直接运用一次函数的性质求解.（2）题目中没有给出一次函数的解析式，而是通过语言、表格和图象给出一次函数的情境，这时需要先根据题目给出的信息求出一次函数的解析式，再利用一次函数的性质求解.知识点2：一次函数的简单应用新知探究注意：应用一次函数解决实际问题的关键是：（1）确定函数与自变量之间的解析式；（2）确定实际问题中自变量的取值范围，即实际问题的答案要符合实际情况.例5“黄金1号”玉米种子的价格为5元/kg，如果一次购买2kg以上的种子，超过2kg部分的种子价格打8折.（1）填写表：购买量/kg0.511.522.533.54⋯付款金额/元⋯2.557.51012141618（2）写出付款金额关于购买量的函数解析式，并画出函数图象.分析：付款金额与种子价格相关，问题中种子价格不是固定不变的，它与购买量有关.设购买xkg种子，当0≤x≤2时，种子价格为5元/kg；当x＞2时，其中有2kg种子按5元/kg计价，其余的（x-2）kg(即超出2kg部分)种子按4元/kg（即8折）计价.因此，写函数解析式与画（2）设购买量为xkg，付款金额为y元.当0≤x≤2时，y=5x.当x＞2时，y=4（x-2）+10=4x+2.函数图象如图所示.y与x的函数解析式也可以合起来表示为（1）一次购买1.5kg种子，需付款多少元？（2）一次购买3kg种子，需付款多少元？1.55=7.5(元).34+2=14(元).7.514思考你能由上面的函数解析式解决以下问题吗？由函数图象也能解决这些问题吗？已知一次函数的图象经过两点（1，4）,（-1，0），求这个一次函数的解析式.跟踪训练新知探究设该一次函数的解析式为y=kx+b（k≠0）想将(1，4),(-1，0)代入k+b=4,-k+b=0k=2,b=2解析式为y=2x+2问题1怎样选取上网收费方式？收费方式月使用费/元包时上网时间/h超时费/(元/min)A30250.05B50500.05C120不限时下表中给出A，B，C三种上宽带网的收费方式.选择哪种方式能节省上网费用？新知探究思考1上表中哪些方式上网费用是变化的，哪些是不变的？思考2A，B方式中上网费用是怎样构成的？解：A，B方式的上网费用是随着时间的变化而变化的，C方式的上网费用是不变的.解：A,B方式的上网费用是由月使用费用+超时费用构成的.思考3设上网时间为xh，则A,B,C三种方式的上网费用分别为y1,y2,y3,其中y1,y2都是关于x的函数，比较以上三种方式哪种方式更优惠应该怎么比较？分析：x代表上网时间，则需要比较在x>0的范围内，y1,y2,y3的大小关系，费用最少的，即为最优惠的.解：从表中可以看出：当0≤x≤25时，y1=30.收费方式月使用费/元包时上网时间/h超时费/(元/min)A30250.05当x>25时，y1=30+0.0560(x-25)=3x-45.30,(0≤x≤25)3x-45,(x>25)A方式的函数解析式为：y1=从表中可以看出：当0≤x≤50时，y2=50.收费方式月使用费/元包时上网时间/h超时费/(元/min)B50500.05当x>50时，y2=50+0.0560(x-50)=3x-100.50,(0≤x≤50)3x-100,(x>50)B方式的函数解析式为：y2=从表中可以看出：C方式无论上网时间多久，每月只用交一次费用即可.收费方式月使用费/元包时上网时间/h超时费/(元/min)C120不限时C方式的函数解析式为：y3=120(x≥0)在同一坐标系中分别画出A,B,C三种方式的函数图象，并进行比较：从图中可以看出：在直线l1的左侧，A方式最省钱.A方式和B方式在直线l1上有交点，此时有3x-45=50，解得x=31.030502550120y1x上网时间/hy上网费用/元l1y3y2l2从图中可以看出：在直线l1和直线l2之间，B方式最省钱.B方式和C方式在直线l2上有交点，此时有3x-100=120，解得x=73.030502550120y1xyl1y3y2l2上网费用/元上网时间/h从图中可以看出：在直线l2的右侧，C方式最省钱.030502550120y1xyl1y3y2l2上网费用/元上网时间/h（1）当上网时间为0≤x≤31时，选择A方式最省钱；（2）当上网时间为3173时，选择C方式最省钱.问题2怎样租车？甲种客车乙种客车载客量（人/辆）4530租金（元/辆）400280某学校计划在总费用2300元的限额内，租用汽车送234名学生和6名教师集体外出活动，每辆汽车上至少要有1名教师.现有甲、乙两种大客车，它们的载客量和租金如表所示：思考1租车方案有哪几种？解：①单独租用甲种客车；②单独租用乙种客车；③同时租用甲种客车和乙种客车.思考2如果甲、乙都租，你能确定合租车辆的范围吗？解：若单独租用甲种客车，则需要240÷45=5,即至少需要6辆；若单独租用乙种客车，则需要240÷30=8,即至少需要8辆.又每辆汽车上至少要有1名教师，共6名教师，所以最多租用汽车6辆，综上，合租车辆为6辆.解：设租用甲种客车x辆，则租用乙种客车(6-x)辆.租车总费用为y元.从人数上：6名教师和234名学生共计240人，所以甲种客车和乙种客车总共的载客量要≥240.从费用上：学校计划的费用是2300元，所以甲种客车和乙种客车总共的费用要≤2300.思考3请给出最节省费用的租车方案.45x+30(6-x)≥240，400x+280(6-x)≤2300.由题意可得，解得4≤x≤5.甲种客车乙种客车载客量（人/辆）4530租金（元/辆）400280设租用甲种客车x辆，则租用乙种客车(6-x)辆.虽然4≤x≤5，但是根据实际意义，x只能取4或5.由题意可得y=400x+280(6-x)=120x+1680(x=4或5)设租车总费用为y元.方案一：当x=4时,即需租用甲种客车4辆,乙种客车2辆.此时y=1204+1680=2160元.方案二：当x=5时,即需租用甲种客车5辆,乙种客车1辆.此时y=1205+1680=2280元.你能不计算就得出结论吗？综上，选择方案一更划算.由y=120x+1680(x=4或5),可以看出函数值y随着自变量x的增大而增大.因为5>4,所以当x=4时，费用更少.可通过一次函数的性质来判断选择最佳方案实际上是在比较的基础上完成的，在没有学习函数之前，一般是将全部方案一一列举出来，然后根据题意选择一个最佳方案；学习函数之后，我们可以利用函数的性质，直接求出最佳方案.用一次函数选择最佳方案的一般步骤1.析：分析题意，弄清数量关系.2.列：列出函数解析式、不等式或方程.3.求：求出自变量取不同值对应的函数值的大小，或函数的最大（小）值.4.选：结合实际需要选择最佳方案.归纳：解决含多个变量的问题时，可以分析这些变量之间的关系，从中选取一个取值能影响其他变量的值的变量作为自变量，然后根据问题的条件寻求可以反映实际问题的函数，以此作为解决问题的数学模型.一家电信公司提供两种手机月通话方式供用户选择，其中一种有月租，另一种无月租，这两种收费方式的通话费用y（元）与通话时间x（分钟）之间的函数关系如图所示.请你判断下列叙述是否正确.yxl2400O20400l1随堂练习（1）l1描述的是无月租费用的收费方式.（2）l2描述的是有月租费用的收费方式.（3）当每月的通话时间超过400分钟的时候选择有月租的收费方式更省钱.yxl2400O20400l1提示：由图可知，超过400分钟后，直线l1在l2的下面，即l1所描述方式的费用小于l2所描述的方式的费用.一次函数求一次函数解析式应用待定系数法①设；②列；③解；④代.①已知一次函数解析式②题目中未给出一次函数解析式课堂小结步骤1.一次函数的图象经过点（2，1）且与直线y=3x平行，求此函数的解析式.解：∵一次函数的图像与直线y=3x平行，∴可设这个一次函数解析式为y=3x+b.∵一次函数图象经过点（2，1）,∴6+b=1,解得b=-5∴这个一次函数的解析式为y=3x-5.拓展提升2.已知一次函数y=kx+4的图象经过点（-3，-2）.解：（1）把点（-3，-2）的坐标代入y=kx+4，得-3k+4=-2，解得k=2，∴这个一次函数的解析式为y=2x+4.（1）求这个函数的解析式；（2）画出函数的图象；（2）由y=2x+4得，当y=0时，x=-2,当x=0时，y=4.∴一次函数解析式y=2x+4与x轴、y轴的交点坐标分别为（-2，0），（0，4）,经过这两点画出的直线即为所求，如图.y=2x+4（3）∵一次函数解析式为y=2x+4，∴当x=3时，y=23+4=10≠5∴点（3，5）不在此函数的图象上y=2x+4（3）判断点（3，5）是否在此函数的图象上.学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元.（1）求A，B两种奖品的单价；（2）学校准备购买A，B两种奖品共计30个，且A奖品的数量不少于B奖品数量的.请设计出最省钱的购买方案，并说明理由.拓展提升解:（1）设A奖品的单价为x元，B奖品的单价为y所以A奖品的单价为30元，B奖品的单价为15元.根据题意，得解得x=30,y=15.3x+2y=120，5x+4y=210，（1）求A，B两种奖品的单价；学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A奖品和2个B奖品共需120元；购买5个A奖品和4个B奖品共需210元.（2）设购买A奖品a个，则购买B奖品(30-a)个，购买奖品的花费为W元.因为15>0，所以当a取最小值时，W有最小值.由题意可知，W=30a+15(30-a)=15a+450.因为a≥(30-a)，解得a≥.又因为a为正整数,所以当a=8时,W有最小值,此时30-8=22,即购买A奖品8个，购买B奖品22个时最省钱.