第20课时-平行线的判定与性质

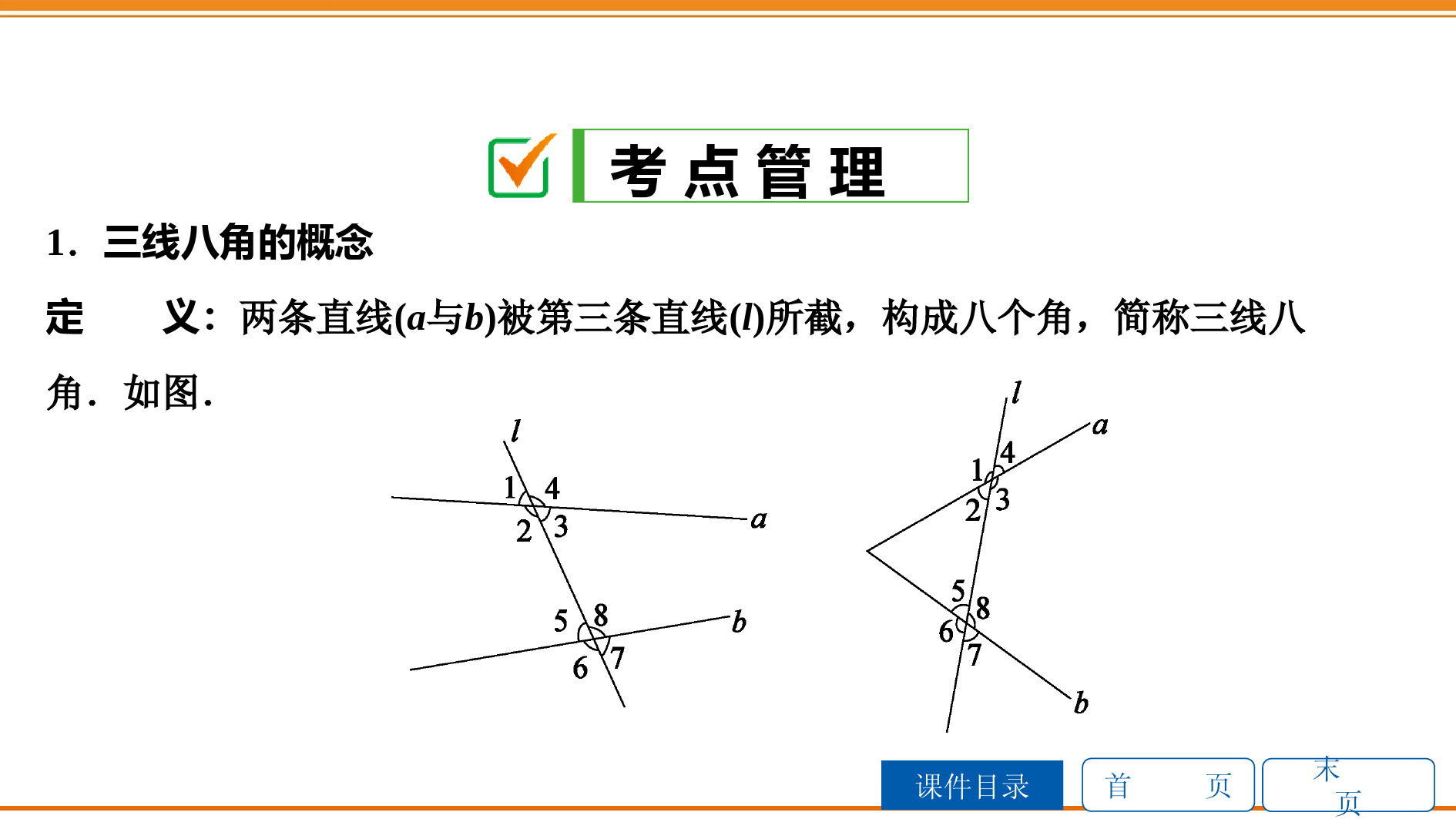
首页课件目录末页第二部分图形与几何第六章线段、角、相交线与平行线考点管理中考再现课时作业归类探究第20课时平行线的判定与性质首页课件目录末页考点管理1．三线八角的概念定义：两条直线(a与b)被第三条直线(l)所截，构成八个角，简称三线八角．如图．首页课件目录末页(1)同位角：如果两个角在截线l的同侧，且在被截直线a，b的同一方向，那么这两个角叫做同位角(位置相同)．∠1和∠5，∠4和∠8，∠2和∠6，∠3和∠7是同位角．(2)内错角：如果两个角在截线l的两旁(交错)，在被截直线a，b之间(内)，那么这两个角叫做内错角(位置在内且交错)．∠2和∠8，∠3和∠5是内错角．(3)同旁内角：如果两个角在截线l的同侧，在被截直线a，b之间(内)，那么这两个角叫做同旁内角．∠2和∠5，∠3和∠8是同旁内角．特点：同位角、内错角和同旁内角都是由三条直线构成的两个角，它们是成对出现的．首页课件目录末页2．平行线定义：在同一平面内不相交的两条直线叫做平行线．平行公理：经过直线外一点，有且只有与这条直线平行．性质：(1)两直线平行，同位角相等；(2)两直线平行，内错角相等；(3)两直线平行，同旁内角互补．一条直线首页课件目录末页判定：(1)同位角相等，两直线平行；(2)内错角相等，两直线平行；(3)同旁内角互补，两直线平行；(4)平行于同一直线的两条直线平行；(5)同一平面内，垂直于同一直线的两条直线平行．注意：只有在同一平面内垂直于同一条直线的两条直线才一定互相平行．首页课件目录末页方法技巧：平行线的性质和判定常用来解决下列问题：(1)画图形的平移；(2)证明线段或角相等；(3)证明两直线平行；(4)证明两直线垂直．首页课件目录末页中考再现1．[2019·邵阳]如图，已知两直线l1与l2被第三条直线l3所截，下列等式一定成立的是()DA．∠1＝∠2B.∠2＝∠3C．∠2＋∠4＝180°D.∠1＋∠4＝180°首页课件目录末页【解析】∠1与∠2是同位角，∠2与∠3是内错角，∠2与∠4是同旁内角，由平行线的性质可知，选项A，B，C成立的条件为l1∥l2，而∠1与∠4是邻补角．故选D.首页课件目录末页2．[2019·长沙]如图，一对平行线AB，CD被直线AE所截，若∠1＝80°，则∠2的度数是()A．80°B.90°C．100°D.110°C首页课件目录末页【解析】如答图，∵∠1＝80°，∴∠3＝100°.∵AB∥CD，∴∠2＝∠3＝100°.故选C.首页课件目录末页3．[2019·衡阳]如图，已知AB∥CD，AF交CD于点E，且BE⊥AF，∠BED＝40°，则∠A的度数是()A．45°B.50°C．80°D.90°B【解析】∵AB∥CD，∴∠B＝∠BED＝40°.∵BE⊥AF，∴∠A＝50°.故选B.首页课件目录末页4．[2019·岳阳]如图，已知BE平分∠ABC，且BE∥DC，若∠ABC＝50°，则∠C的度数是()A．20°B.25°C．30°D.50°B首页课件目录末页【解析】∵BE平分∠ABC，∴∠EBC＝12∠ABC＝12×50°＝25°.∵BE∥DC，∴∠C＝∠EBC＝25°.故选B.首页课件目录末页5．[2019·娄底]如图，AB∥CD，AC∥BD，若∠1＝28°，则∠2的度数为.28°【解析】∵AC∥BD，∠1＝28°，∴∠A＝∠1＝28°.又∵AB∥CD，∴∠2＝∠A＝28°.首页课件目录末页归类探究类型之一平行线的性质[2019·鄂州]如图，一块直角三角板的一个顶点落在直尺的一边上，若∠2＝35°，则∠1的度数为()BA．45°B.55°C．65°D.75°首页课件目录末页【解析】如答图，作EF∥AB∥CD.∴∠2＝∠AEF＝35°，∠1＝∠FEC.∵∠AEC＝90°，∴∠1＝90°－35°＝55°.故选B.首页课件目录末页1．[2019·宜昌]如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α＝135°，则∠β等于()CA．45°B.60°C．75°D.85°首页课件目录末页【解析】如答图，∵∠α＝135°，∴∠1＝45°.∴∠β＝180°－45°－60°＝75°.故选C.首页课件目录末页2．[2019·荆州]已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置(∠ABC＝30°)，其中A，B两点分别落在直线m，n上，若∠1＝40°，则∠2的度数为()A．10°B.20°C．30°D.40°B首页课件目录末页【解析】∵直线m∥n，∴∠2＋∠ABC＋∠1＋∠BAC＝180°.∵∠ABC＝30°，∠BAC＝90°，∠1＝40°，∴∠2＝180°－30°－90°－40°＝20°.故选B.首页课件目录末页3．[2019·原创]如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两块三角板的一直角边重合，含30°角的三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是()A．15°B.22.5°C．30°D.45°A首页课件目录末页【解析】如答图，过点A作AB∥a，则∠1＝∠2.∵a∥b，∴AB∥b.∴∠3＝∠4＝30°.而∠2＋∠3＝45°，∴∠2＝15°.∴∠1＝15°.故选A.【点悟】两直线平行是确定等角的一个重要途径，证明两角相等，常从判断它们所处的“三线八角”中的直线是否平行来入手．首页课件目录末页类型之二平行线的判定与性质的综合运用[2019·济宁]如图，直线a，b被直线c，d所截，若∠1＝∠2，∠3＝125°，则∠4的度数是()A．65°B.60°C．55°D.75°C首页课件目录末页【解析】如答图．∵∠1＝∠2，∴a∥b，∴∠3＝∠5＝125°，∴∠4＝180°－∠5＝180°－125°＝55°.故选C.首页课件目录末页4．[2019·凉山]如图，BD∥EF，AE与BD交于点C，∠B＝30°，∠A＝75°，则∠E的度数为()DA．135°B.125°C．115°D.105°【解析】∵∠ACD＝∠A＋∠B＝30°＋75°＝105°，且BD∥EF，∴∠E＝∠ACD＝105°.故选D.首页课件目录末页5．[2019·泰安]如图，直线l1∥l2，∠1＝30°，则∠2＋∠3＝()A．150°B.180°C．210°D.240°C首页课件目录末页【解析】如答图，过点A作l3∥l1.∵l1∥l2，∴l2∥l3，∴∠4＝∠1＝30°，∠5＋∠3＝180°，∴∠2＋∠3＝∠4＋∠5＋∠3＝210°.故选C.首页课件目录末页类型之三平行线的开放探究型问题已知平面内的两条直线有相交和平行两种位置关系．首页课件目录末页(1)如图①，若AB∥CD，点P在AB，CD外部，则有∠B＝∠BOD.又∵∠BOD是△POD的外角，∴∠BOD＝∠BPD＋∠D，得∠BPD＝∠B－∠D.若将点P移到AB，CD内部，如图②，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD，∠B，∠D之间有何数量关系？请证明你的结论；(2)在图②中，将直线AB绕点B逆时针方向旋转一定角度，交直线CD于点Q，如图③，则∠BPD，∠B，∠D，∠BQD之间有何数量关系？(不需证明)(3)根据(2)的结论求图④中∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．首页课件目录末页解：(1)不成立，结论：∠BPD＝∠B＋∠D.例3答图证明：如答图，延长BP，交CD于点E.∵AB∥CD，∴∠B＝∠BED.又∵∠BPD＝∠BED＋∠D，∴∠BPD＝∠B＋∠D.(2)结论：∠BPD＝∠BQD＋∠B＋∠D.首页课件目录末页(3)设AC与BF相交于点G(图略)．由(2)的结论，得∠AGB＝∠A＋∠B＋∠E.又∵∠AGB＝∠CGF，且∠CGF＋∠C＋∠D＋∠F＝360°，∴∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝360°.首页课件目录末页【点悟】本题属于探索型题目，解题的关键是由图形提供的信息，探索、猜想、归纳出在不同位置上各角之间的变化规律．这是近几年中考中的创新型试题．首页课件目录末页课时作业(72分)一、选择题(每题5分，共25分)1．[2018·金华]如图，∠B的同位角是()A．∠1B.∠2C．∠3D.∠4D首页课件目录末页2．[2018·郴州]如图，直线a，b被直线c所截．下列条件中，不能判定a∥b的是()A．∠2＝∠4B.∠1＋∠4＝180°C．∠5＝∠4D.∠1＝∠3D首页课件目录末页3．[2019·滨州]如图，AB∥CD，∠FGB＝154°，FG平分∠EFD，则∠AEF的度数等于()A．26°B.52°C．54°D.77°B首页课件目录末页【解析】∵AB∥CD，∴∠DFG＋∠FGB＝180°.∵∠FGB＝154°，∴∠DFG＝26°.∵FG平分∠EFD，∴∠EFD＝2∠DFG＝2×26°＝52°.∵AB∥CD，∴∠AEF＝∠EFD＝52°.故选B.首页课件目录末页4．[2019·河南]如图，AB∥CD，∠B＝75°，∠E＝27°，则∠D的度数为()A．45°B.48°C．50°D.58°B首页课件目录末页【解析】∵AB∥CD，∠B＝75°，∴∠B＝∠CFE＝75°.∵∠CFE＝∠D＋∠E，∠E＝27°，∴∠D＝∠CFE－∠E＝75°－27°＝48°.故选B.首页课件目录末页5．[2019·山西]如图，在△ABC中，AB＝AC，∠A＝30°，直线a∥b，顶点C在直线b上，直线a交AB于点D，交AC于点E，若∠1＝145°，则∠2的度数是()CA．30°B.35°C．40°D.45°首页课件目录末页【解析】△ABC中，AB＝AC，∠A＝30°，∴∠B＝75°.∵∠1＝145°，∴∠EDB＝145°.如答图，过点B作BG∥a∥b，∴∠EDB＋∠DBG＝180°，∠2＝∠CBG.∵∠ABC＝∠DBG＋∠CBG，∴∠2＝75°－35°＝40°.故选C.首页课件目录末页二、填空题(每题6分，共24分)6．[2019·菏泽]如图，AD∥CE，∠ABC＝100°，则∠2－∠1的度数是.80°首页课件目录末页【解析】如答图，过点B作BF∥AD.∵AD∥CE，∴AD∥BF∥CE，∴∠1＝∠3，∠4＋∠2＝180°，∠3＋∠4＝100°，∴∠1＋∠4＝100°，∠2＋∠4＝180°，∴∠2－∠1＝80°.首页课件目录末页7．[2018·通辽]如图，∠AOB的一边OA为平面镜，∠AOB＝37°45′，在OB边上有一点E，从点E射出一束光线经平面镜反射后，反射光线DC恰好与OB平行，则∠DEB的度数是．75°30′(或75．5°)首页课件目录末页【解析】如答图，过点D作DF⊥AO，交OB于点F.∵反射角等于入射角，∴∠1＝∠2.∴∠ADC＝∠ODE.∵CD∥OB，∠ADC＝∠AOB.∴∠DEB＝∠AOB＋∠ODE＝2∠AOB＝75°30′.首页课件目录末页8．[2019·绵阳]如图，AB∥CD，∠ABD的平分线与∠BDC的平分线交于点E，则∠1＋∠2＝.90°首页课件目录末页【解析】∵AB∥CD，∴∠ABD＋∠CDB＝180°.∵BE是∠ABD的平分线，∴∠1＝12∠ABD.∵DE是∠BDC的平分线，∴∠2＝12∠CDB，∴∠1＋∠2＝90°.首页课件目录末页9．[2018·衡阳]将一副三角板如图放置，使点A落在DE上．若BC∥DE，则∠AFC的度数为.75°首页课件目录末页【解析】∵BC∥DE，∴∠ECB＝∠E＝30°.∵∠ABC＝45°，∴∠AFC＝∠ABC＋∠ECB＝45°＋30°＝75°.首页课件目录末页三、解答题(共23分)10．(11分)[2018·益阳]如图，AB∥CD，∠1＝∠2.求证：AM∥CN.首页课件目录末页证明：∵AB∥CD，∴∠EAB＝∠ACD.∵∠1＝∠2，∴∠EAB－∠1＝∠ACD－∠2，即∠EAM＝∠ACN.∴AM∥CN.首页课件目录末页11．(12分)[2019·武汉]如图，点A，B，C，D在一条直线上，CE与BF交于点G，∠A＝∠1，CE∥DF.求证：∠E＝∠F.首页课件目录末页证明：∵∠A＝∠1，∴AE∥BF，∴∠E＝∠2.∵CE∥DF，∴∠F＝∠2.∴∠E＝∠F.首页课件目录末页(12分)12．(12分)如图，已知l1∥l2，点C1在直线l1上，并且C1A⊥l2，A为垂足，C2，C3是l1上任意两点，点B在l2上．设△ABC1的面积为S1，△ABC2的面积为S2，△ABC3的面积为S3，小颖认为S1＝S2＝S3，请帮小颖说明理由．首页课件目录末页解：∵直线l1∥l2，∴△ABC1，△ABC2，△ABC3的底边AB上的高相等．∴△ABC1，△ABC2，△ABC3这3个三角形同底等高．∴△ABC1，△ABC2，△ABC3这3个三角形的面积相等，即S1＝S2＝S3.首页课件目录末页(16分)13．(16分)如图，AB∥CD，分别探讨四个图形中∠APC与∠PAB，∠PCD的关系．请你从所得到的关系中任选一个加以证明．首页课件目录末页解：∠①APC＝∠PAB＋∠PCD；∠②APC＝360°－(∠PAB＋∠PCD)；∠③APC＝∠PAB－∠PCD；∠④APC＝∠PCD－∠PAB.如证明∠①APC＝∠PAB＋∠PCD.首页课件目录末页证明：如答图，过点P作PE∥AB，则∠PAB＝∠APE.又∵AB∥CD，∴PE∥CD.∴∠PCD＝∠CPE.∴∠PAB＋∠PCD＝∠APE＋∠CPE.∴∠APC＝∠PAB＋∠PCD.