平行线分线段成比例(课件)-2022-2023学年九年级数学上册同步精品课堂(北师大版)

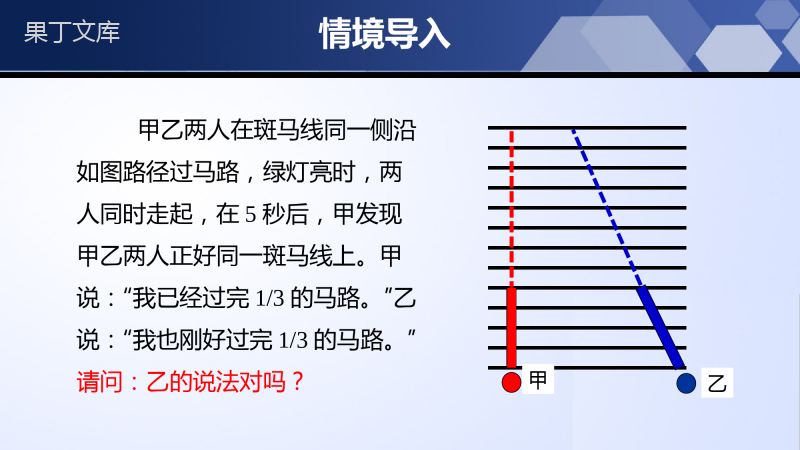
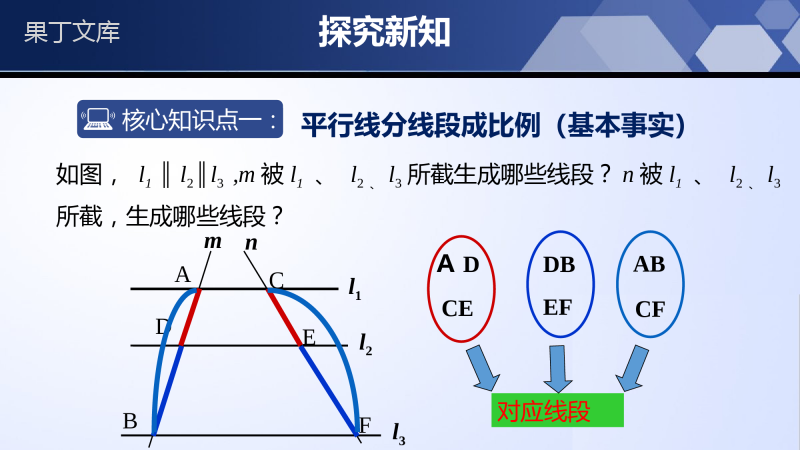
新课标北师大版九年级上册第四章图形的相似4.2平行线分线段成比例学习目标1、掌握平行线分线段成比例的基本事实及其推论。2、能熟练运用平行线分线段成比例的基本事实及其推论计算线段的长度。情境导入一、比例的基性质：（1）如果，那么（2）如果（a、b、c、d都不等于0），那么acbdadbcadbcacbd二、合比性质、等比性质：如果，那么和；如果那么；acbd+abcdbd--abcdbd==(0)acmbdnbdn++acmabdnb情境导入甲乙两人在斑马线同一侧沿如图路径过马路，绿灯亮时，两人同时走起，在5秒后，甲发现甲乙两人正好同一斑马线上。甲说：“我已经过完1/3的马路。”乙说：“我也刚好过完1/3的马路。”请问：乙的说法对吗？甲乙探究新知核心知识点一：平行线分线段成比例（基本事实）ADBl1l2l3mFECnＡDDBABCEEFCF对应线段如图，l1∥l2∥l3,m被l1、l2、l3所截生成哪些线段？n被l1、l2、l3所截，生成哪些线段？探究新知1223AAAA1223BBBB如图，小方格的边长为1，l1∥l2∥l3，则：＝________，＝________.发现：____________________.141412122323AABBAABB探究新知3232将l2向下平移至如图所示的位置，则：＝________，＝________.发现：____________________.1223AAAA1223BBBB12122323AABBAABB探究新知思考：1、上面我们探究的是在方格纸上的特殊情况，如果不在方格纸上上面的结论还成立吗？2、在平面上任意作三条平行线，用他们截两条直线，截得的线段成比例吗？试着在纸上画一画！探究新知归纳总结平行线分线段成比例定理：一般地，我们有平行线分线段成比例的基本事实：两条直线被一组平行线所截，所得的对应线段成比例.数学表达式：如图，∵l3l∥4l∥5，∴=，=，=.可简记为：=，=，=.探究新知注意：1.一组平行线两两平行，被截直线不一定平行；2.所有的成比例线段是指被截直线上的线段，与这组平行线上的线段无关；3.对应线段成比例是指同一直线上的两条线段的比等于另一条直线上与它们对应的线段的比。探究新知例:如图，已知l1l∥2l∥3，下列比例式中错误的是()A.B.C.D.DFBDCEAC=BFBDAEAC=BFDFAEAC=ACBDBFAE=D探究新知核心知识点二：平行线分线段成比例定理的推论ABCDEFabc如图，直线abc∥∥，由平行线分线段成比例的基本事实，我们可以得出图中对应成比例的线段，把直线n向左或向右任意平移，这些线段是否依然成比例呢？思考：平移的过程中，能否得到特殊的模型？如果有，请画出来。探究新知核心知识点二：平行线分线段成比例定理的推论如图，直线abc∥∥，由平行线分线段成比例的基本事实，我们可以得出图中对应成比例的线段，把直线n向左或向右任意平移，这些线段是否依然成比例呢？思考：平移的过程中，能否得到特殊的模型？如果有，请画出来。ABCDEFabc探究新知核心知识点二：平行线分线段成比例定理的推论如图，直线abc∥∥，由平行线分线段成比例的基本事实，我们可以得出图中对应成比例的线段，把直线n向左或向右任意平移，这些线段是否依然成比例呢？思考：平移的过程中，能否得到特殊的模型？如果有，请画出来。ABCDEFabc探究新知ABCDEABCDEABCDE思考：下列模型中，平行线分线段成比例的结论还能成立吗？探究新知归纳总结平行于三角形一边的直线与其他两边相交，截得的对应线段成比例.平行线分线段成比例基本事实的推论：数学表达式：如图，若DEBC∥，则有=或=或=.探究新知例：如图，在△ABC中，E，F分别是AB和AC上的点，且EF∥BC.(1)如果AE=7，EB=5，FC=4，那么AF的长是多少？(2)如果AB=10，AE=6，AF=5，那么FC的长是多少？ABCEF解:(1)∵EF∥BC，AEAFEBFC∴————，＝7AF54————，＝即＝285——.∴AF探究新知例：如图，在△ABC中，E，F分别是AB和AC上的点，且EF∥BC.(1)如果AE=7，EB=5，FC=4，那么AF的长是多少？(2)如果AB=10，AE=6，AF=5，那么FC的长是多少？ABCEF解:(2)AEAFABAC∴————，＝6510AC————.＝即＝253——，∴AC＝103—.∴FC想一想：怎样利用平行线分线段成比例的基本事实求线段长？先确定图中的平行线，由此联想到线段间的比例关系，结合待求线段和已知线段写出一个含有它们的比例式，构造出方程，解方程求出待求线段长．探究新知随堂练习D1.如图，若l1∥l2∥l3，则下列各式不一定成立的是()A.B.C.D.ACBDCEDFAEBFCEDFACBDAEBFAEBFACDF随堂练习2.如图，DE∥FG∥BC，若DB＝4FB，则EG与GC的关系是()A．EG＝4GCB．EG＝3GCC．EG＝5GCD．EG＝2GCB随堂练习3.如图，直线l1∥l2∥l3，直线AC和DF被l1，l2，l3所截，AB＝5，BC＝6，EF＝4，则DE的长为()A．2B．3C．4D．103D随堂练习4.如图，直线a∥b∥c，直线l1、l2与这三条平行线分别交于点A，B，C和点D，E，F.若AB∶BC＝12∶，EF＝6，则DE的长为________．3随堂练习5.如图，DE∥BC.(1)若AD＝BD＝2，AE＝3，则CE＝________；(2)若AD＝3，AB＝5，AE＝4，求CE的长．3解：∵DE∥BC，∴＝，即＝∴AC＝又∵AC＝AE＋CE∴CE＝AC－AE＝－4＝ADABAEAC4AC2032038335随堂练习6.如图，EG∥BC，GF∥DC，AE＝3，EB＝2，AF＝6，求AD的值．解：∵EG∥BC∴＝＝又∵GF∥DC∴＝∴＝∴FD＝AF＝×6＝4∴AD＝AF＋FD＝6＋4＝10AGCGAEEB32AGCGAFFDAFFD322323随堂练习7.如图，在△ABC中，D，E，F分别是AB，AC，BC上的点，且DE∥BC，EF∥AB，AD∶DB＝23∶，BC＝20cm，求BF的长解：∵DE∥BC，EF∥AB，∴四边形BDEF是平行四边形，∴BF＝DE，∵AD∶DB＝23∶，∴AD∶AB＝25.∶∵DE∥BC，∴DE∶BC＝AD∶AB＝25∶，即DE20∶＝25∶，∴DE＝8，∴BF＝8.故BF的长为8cm.课堂小结【平行线分线段成比例定理】两条直线被一组平行线所截，所得到的对应线段成比例平行线分线段成比例定理的符号语言：若a//b//c，则.12122323=AABBAABB【推论】平行于三角形一边的直线与其他两边（或者两边的延长边）相交，截得的对应线段成比例谢谢~