双曲线的参数方程,双曲线的参数方程公式

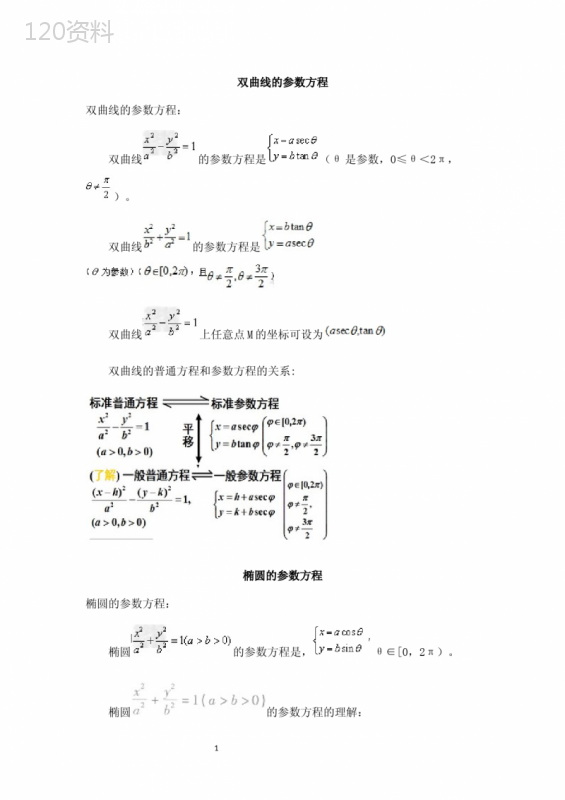
('1双曲线的参数方程双曲线的参数方程：双曲线的参数方程是（θ是参数，0≤θ＜2π，）。双曲线的参数方程是双曲线上任意点M的坐标可设为双曲线的普通方程和参数方程的关系:椭圆的参数方程椭圆的参数方程：椭圆的参数方程是，θ∈[0，2π）。椭圆的参数方程的理解：2如图，以原点为圆心，分别以a，b（a>b>0）为半径作两个圆，点B是大圆半径OA与小圆的交点，过点A作AN⊥Ox，垂足为N，过点B作BM⊥AN，垂足为M，求当半径OA绕点O旋转时，点M的横坐标与点A的横坐标相同，点M的纵坐标与点B的纵坐标相同．而A、B的坐标可以通过引进参数建立联系．设，由已知得，即为点M的轨迹参数方程，消去参数得，即为点M的轨迹普通方程。(1)参数方程，是椭圆的参数方程；(2)在椭圆的参数方程中，常数a、b分别是椭圆的长半轴长和短半轴长．a>b,称为离心角，规定参数的取值范围是[0，2π）;(3)焦点在y轴的参数方程为曲线的参数方程曲线的参数方程的定义：一般地，在平面直角坐标系中，如果曲线C上任意一点的坐标x、y都是某个变数t的函数，并且对于t的每一个允许值，由方程组①所确定的点P（x，y）都在这条曲线C上，那么方程组①就叫做这条曲线的参数方程。变数t叫做参变量或参变数，简称参数。3曲线的参数方程的理解与认识：（1）参数方程的形式：横、纵坐标x、y都是变量t的函数，给出一个t能唯一的求出对应的x、y的值，因而得出唯一的对应点；但横、纵坐标x、y之间的关系并不一定是函数关系。（2）参数的取值范围：在表述曲线的参数方程时，必须指明参数的取值范围；取值范围的不同，所表示的曲线也可能会有所不同。（3）参数方程与普通方程的统一性：普通方程是相对参数方程而言的，普通方程反映了坐标变量x与y之间的直接联系，而参数方程是通过变数反映坐标变量x与y之间的间接联系；普通方程和参数方程是同一曲线的两种不同表达形式；参数方程可以与普通方程进行互化。圆的参数方程圆的参数方程：（θ∈[0，2π）），（a，b）为圆心坐标，r为圆的半径，θ为参数（x，y）为经过点的坐标。圆心为原点，半径为r的圆的参数方程：如图，如果点P的坐标为(x，y)，圆半径为r，根据三角函数定义，点P的横坐标x、纵坐标y都是θ的函数，即4参数方程的概念参数方程的概念：一般地，在给定的平面直角坐标系中，如果曲线上任意一点的坐标x，y都是某个变数t的函数且对于t的每一个允许值，由这个方程组所确定的点M（x，y）都在这条曲线上，那么这个方程组称为这条曲线的参数方程，联系x、y之间关系的变数t称为参变数，简称参数。相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程．参数方程和普通方程的互化：在参数方程与普通方程的互化中，必须使x，y的取值范围保持一致．否则，互化就是不等价的。（1）参数方程化为普通方程的过程就是消参过程，常见方法有三种：①代入法：利用解方程的技巧求出参数t，然后代入消去参数；②三角法：利用三角恒等式消去参数；③整体消元法：根据参数方程本身的结构特征，从整体上消去．(2)普通方程化为参数方程需要引入参数．如：①直线的普通方程是2x-y+2=0，可以化为参数方程5②在普通方程xy=1中，令可以化为参数方程关于参数的几点说明：(1)参数是联系变数x，y的桥梁，可以是一个有物理意义或几何意义的变数，也可以是没有明显实际意义的变数．(2)同一曲线选取参数不同，曲线参数方程形式也不同．(3)在实际问题中要确定参数的取值范围．参数方程的几种常用方法：方法1参数方程与普通方程的互化：将曲线的参数方程化为普通方程的方法应视题目的特点而定，要选择恰当的方法消参，并要注意由于消参后引起的范围限制消失而造成的增解问题．常用的消参技巧有加减消参，代人消参，平方消参等．方法2求曲线的参数方程：求曲线的参数方程或应用曲线的参数方程，要熟记曲线参数方程的形式及参数的意义．方法3参数方程问题的解决方法：解决参数方程的一个基本思路是将其转化为普通方程，然后利用在直角坐标系下解决问题的方式进行解题．方法4利用圆的渐开线的参数方程求点：利用参数方程求解点时只需将参数代入方程就可求得。方法5求圆的摆线的参数方程：根据圆的摆线的参数方程的表达式，可知只需求出其中的r，也就是说，摆线的参数方程由圆的半径唯一确定，因此只需把点代人参数方程求出r值再代人参数方程的表达式．',)