《双曲线及标准方程》人教版高中数学选修2-1PPT课件（第2.3.1课时）.pptx

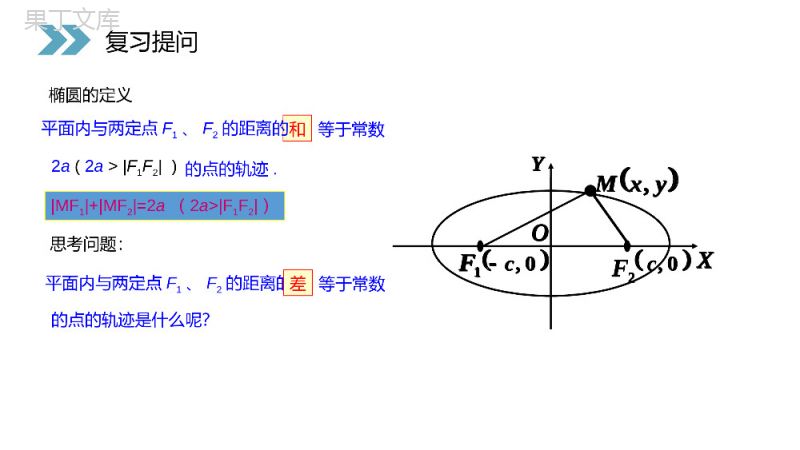
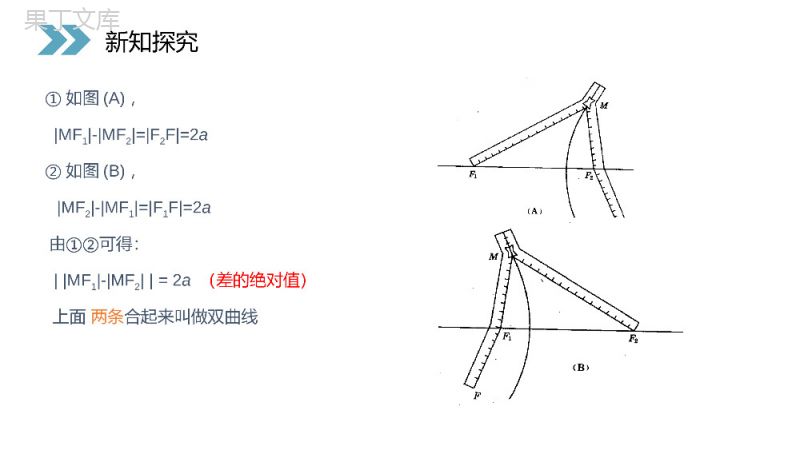
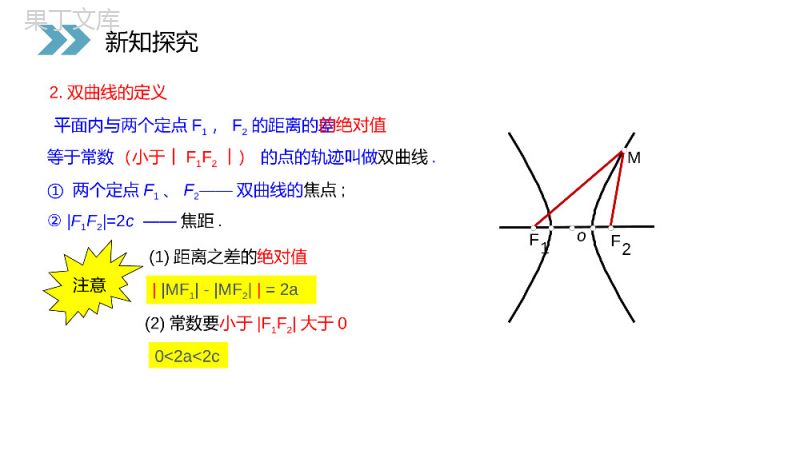
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-12.3.1双曲线及标准方程第2章圆锥曲线与方程人教版高中数学选修2-1椭圆的定义和等于常数2a(2a>F1F2)的点的轨迹.平面内与两定点F1、F2的距离的1F2F0,c0,cXYOyxM,思考问题：平面内与两定点F1、F2的距离的差等于常数的点的轨迹是什么呢？MF1+MF2=2a（2a>F1F2）复习提问1F2F0,c0,cXYOyxM,P={MMF1-MF2=2a}P={MMF1-MF2=2a}P={MMF1-MF2=－2a}1.画双曲线新知探究①如图(A)，②如图(B)，上面两条合起来叫做双曲线由①②可得：MF1-MF2=2a（差的绝对值）MF2-MF1=F1F=2aMF1-MF2=F2F=2a新知探究①两个定点F1、F2——双曲线的焦点;②F1F2=2c——焦距.oF2F1M平面内与两个定点F1，F2的距离的差等于常数的点的轨迹叫做双曲线.的绝对值（小于︱F1F2︱）注意MF1-MF2=2a2.双曲线的定义(1)距离之差的绝对值(2)常数要小于F1F2大于00<2a<2c新知探究试说明在下列条件下动点M的轨迹各是什么图形？（F1、F2是两定点,F1F2=2c(02c，动点M的轨迹.新知探究oF2FM1MF1-MF2=2aMF2-MF1=2aMF1-MF2=2a（差的绝对值）M即双曲线的左支即双曲线的右支即表示整个双曲线当MF1-MF2=2a时，M点轨迹是双曲线中靠近F2的一支；当MF2-MF1=2a时，M点轨迹是双曲线中靠近F1的一支.新知探究如何求这优美的曲线的方程？新知探究xyo设M（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)F1F2M以F1,F2所在的直线为X轴，线段F1F2的中点为原点建立直角坐标系即(x+c)2+y2-(x-c)2+y2=+2a_1.建系.2.设点．3.列式．MF1-MF2=2a4.化简.3.双曲线的标准方程新知探究2222(xc)y(xc)y2a222222((xc)y)((xc)y2a)222cxaa(xc)y22222222(ca)xaya(ca)令c2－a2=b22222xy1abyoF1M新知探究2222(xc)y(xc)y2a222222((xc)y)((xc)y2a)222cxaa(xc)y22222222(ca)xaya(ca)2222xy1ab12222byax12222bxayF2F1MxOyOMF2F1xy)00(ba，双曲线的标准方程新知探究12222byax12222bxay)00(ba，已知F1(-4,0)，F2(4,0),︱MF1︱－︱MF2︱=2a,当a=3和4时，点M轨迹分别为（）A.双曲线和一条直线B.双曲线和两条射线C.双曲线一支和一条直线D.双曲线一支和一条射线练一练:新知探究双曲线的标准方程与椭圆的标准方程有何区别与联系?新知探究新知探究定义方程焦点a.b.c的关系F（±c，0）F（±c，0）a>0，b>0，但a不一定大于b，c2=a2+b2c最大a>b>0，c2=a2-b2a最大双曲线与椭圆之间的区别与联系MF1－MF2=2aMF1+MF2=2a椭圆双曲线F（0，±c）F（0，±c）22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab判断：与的焦点位置？221169xy221916yx思考：如何由双曲线的标准方程来判断它的焦点是在X轴上还是Y轴上？结论：看前的系数，哪一个为正，则在哪一个轴上。22,yx新知探究221169xy221916yx22,yx解：(1)(2)0mm12mm或1032012212mmmmmm且1.已知方程表示椭圆，则的取值范围是____________.22112xymmm若此方程表示双曲线，的取值范围？m解：4.例题讲解课堂练习(1)(2)0mm12mm或1032012212mmmmmm且22112xymmmm22(2)33a=b=c=xy则焦点坐标为2.已知下列双曲线的方程：22(1)1a=b=c=916yx则焦点坐标为345(0,-5),(0,5)312(-2,0),(2,0)课堂练习22(2)33a=b=c=xy则焦点坐标为22(1)1a=b=c=916yx则焦点坐标为3解：由双曲线的定义知点的轨迹是双曲线.因为双曲线的焦点在轴上，所以设它的标准方程为所求双曲线的方程为：2223,,259165abcac2c=10由已知2a=6221916xyP3.已知,动点到、的距离之差的绝对值为6，求点的轨迹方程.12(5,0),(5,0)FFP1F2FP22221(0,0)xyababx课堂练习2223,,259165abcac2c=10由已知2a=6221916xyP12(5,0),(5,0)FFP1F2FP22221(0,0)xyababx4.写出适合下列条件的双曲线的标准方程(1)a=4,b=3,焦点在x轴上;(2)焦点为F1(0,-6),F2(0,6),过点M(2,-5)利用定义得2a=MF1－MF24103(3)a=4,过点(1,)分类讨论课堂练习15(4)P(-2,-3)Q(,2).3焦点在x轴上，且过，15(4)P(-2,-3)Q(,2).3变式：过，221(0,0)mxnymn由题可设双曲线的方程为：410315(4)P(-2,-3)Q(,2).3焦点在x轴上，且过，15(4)P(-2,-3)Q(,2).3变式：过，221(0,0)mxnymn由题可设双曲线的方程为：222bac定义图象方程焦点a.b.c的关系MF1-MF2=2a（０<2a0，b>0，但a不一定大于b，c2=a2+b2c最大a>b>0，c2=a2-b2a最大双曲线与椭圆之间的区别与联系MF1－MF2=2aMF1+MF2=2a椭圆双曲线F（0，±c）F（0，±c）22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab课堂小结22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第2章圆锥曲线与方程人教版高中数学选修2-1