双曲线的定义及其标准方程,双曲线的定义及其标准方程教学设计

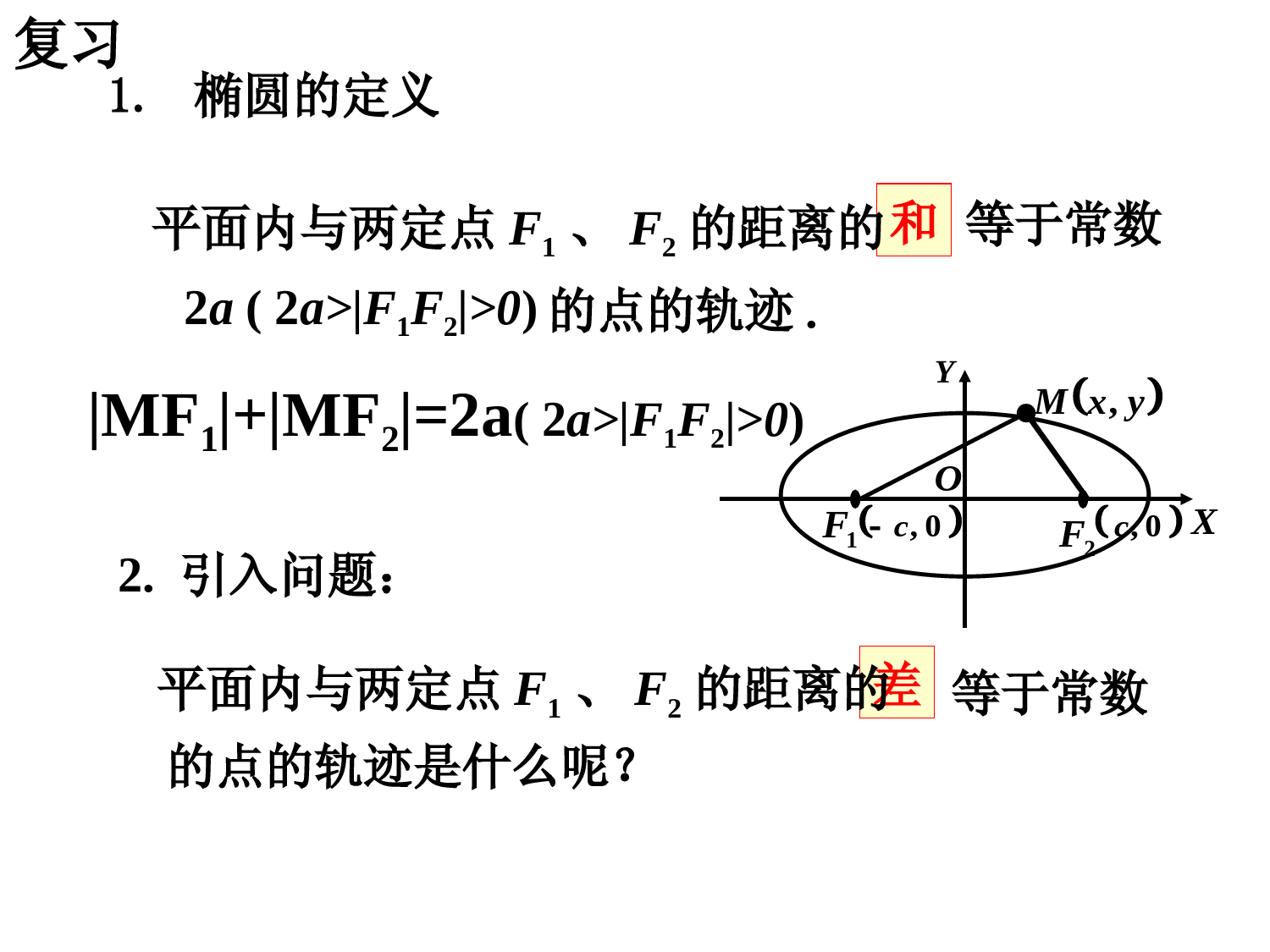
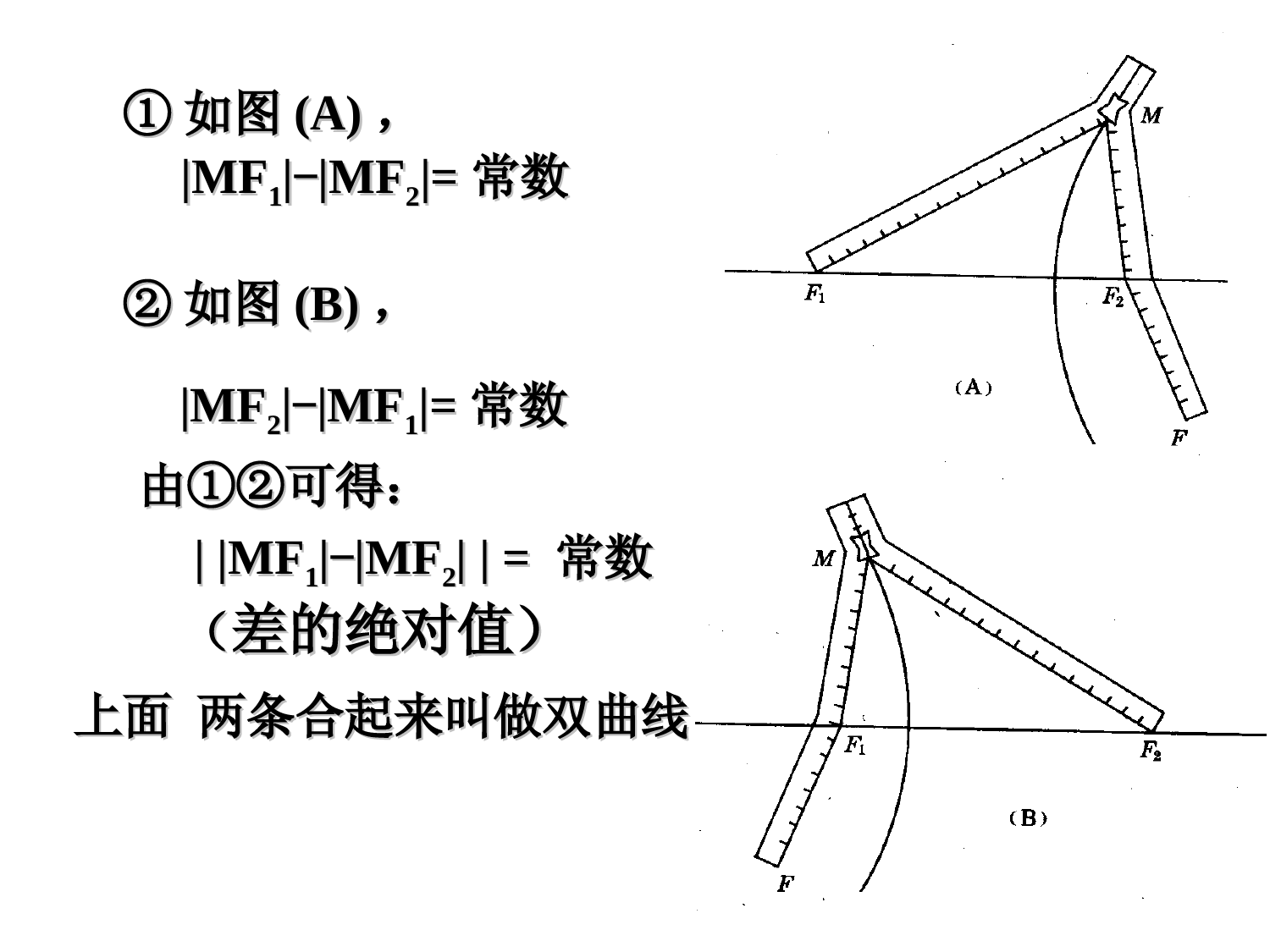
双曲线及其标准方程1.椭圆的定义和等于常数2a(2a>F1F2>0)的点的轨迹.平面内与两定点F1、F2的距离的1F2F0,c0,cXYOyxM,2.引入问题：差等于常数的点的轨迹是什么呢？平面内与两定点F1、F2的距离的复习MF1+MF2=2a(2a>F1F2>0)①①如图如图(A)(A)，，MFMF11--MFMF22==常数常数②②如图如图(B)(B)，，上面两条合起来叫做双曲线上面两条合起来叫做双曲线由①②可得：由①②可得：MFMF11--MFMF22==常数常数（（差的绝对值）差的绝对值）MFMF22--MFMF11==常数常数双曲线在生活中☆.☆①两个定点F1、F2——双曲线的焦点;②F1F2=2c——焦距.（1）2a0；双曲线定义思考：（1）若2a=F1F2,则轨迹是？（2）若2a>F1F2,则轨迹是？说明（3）若2a=0,则轨迹是？MF1-MF2=2a(1)两条射线(2)不表示任何轨迹(3)(3)线段线段FF11FF22的垂直平分线的垂直平分线如何建立适当的直角坐标系？原则：尽可能使方程的形式简单、运算简单；(一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴.)♦探讨建立平面直角坐标系的方案OxyOxyOxy方案一Oxy(对称、“简洁”)1F2FMOxy方案二F2F1MxOy求曲线方程的步骤：双曲线的标准方程1.建系.以F1,F2所在的直线为x轴，线段F1F2的中点为原点建立直角坐标系2.设点．设M（x,y）,则F1(-c,0),F2(c,0)3.列式MF1-MF2=±2a4.化简aycxycx2)()(2222即aycxycx2)()(2222222222)(2)(ycxaycx222)(ycxaacx)()(22222222acayaxac222bac)0,0(12222babyax此即为焦点在x轴上的双曲线的标准方程12222byax12222bxayF2F1MxOyOMF2F1xy)00(ba，若建系时,焦点在y轴上呢?看前的系数，哪一个为正，则在哪一个轴上22,yx22、双曲线的标准方程与椭圆的标准方程有何区、双曲线的标准方程与椭圆的标准方程有何区别与联系别与联系??11、如何判断双曲线的焦点在哪个轴上？、如何判断双曲线的焦点在哪个轴上？问题问题学习小结:222bac双曲线定义双曲线定义双曲线图象双曲线图象标准方程标准方程焦点焦点aa..bb..cc的关系的关系MF1-MF2=2a（０<2a0，b>0，但a不一定大于b，c2=a2+b2a>b>0，a2=b2+c2双曲线与椭圆之间的区别与联系双曲线与椭圆之间的区别与联系MF1－MF2=2aMF1+MF2=2a椭圆双曲线F（0，±c）F（0，±c）22221(0)xyabab22221(0)yxabab22221(0,0)xyabab22221(0,0)yxabab双曲线的焦点且垂直x轴的弦的长度为.14322yx338-2x2=1的焦点为、焦距是.),(2606练习巩固:3.方程(2+)x2+(1+)y2=1表示双曲线的充要条件是.-2<<-1双曲线及其标准方程(一)4)3()3()1(2222yxyx5)3()3()2(2222yxyx6)3()3()3(2222yxyx方程表示的曲线是双曲线方程表示的曲线是双曲线的右支方程表示的曲线是x轴上分别以F1和F2为端点，指向x轴的负半轴和正半轴的两条射线。练习巩固:下列方程各表示什么曲线?例2题型二利用双曲线的定义求轨迹问题动圆M与圆C1：(x＋3)2＋y2＝9外切，且与圆C2：(x－3)2＋y2＝1内切，求动圆圆心M的轨迹方程．【解】∵圆M与圆C1外切，且与圆C2内切，∴MC1＝R＋3，MC2＝R－1，∴MC1－MC2＝4.∴点M的轨迹是以C1、C2为焦点的双曲线的右支，且有a＝2，c＝3，b2＝c2－a2＝5，∴所求轨迹方程为x24－y25＝1(x≥2)．【名师点评】利用定义法求双曲线的标准方程，首先找出两个定点(即双曲线的两个焦点)；然后再根据条件寻找动点到两个定点的距离的差(或差的绝对值)是否为常数，这样确定c和a的值，再由c2＝a2＋b2求b2，进而求双曲线的方程．解：∴126PFPF∵焦点为12(5,0),(5,0)FF∴可设所求方程为:22221xyab(a>0,b>0).∵2a=6,2c=10,∴a=3,c=5.所以点P的轨迹方程为221916xy.∵1210FF>6,由双曲线的定义可知，点P的轨迹是一条双曲线,例1已知两定点1(5,0)F,2(5,0)F,动点P满足126PFPF,求动点P的轨迹方程.变式训练1:已知两定点1(5,0)F,2(5,0)F,动点P满足126PFPF,求动点P的轨迹方程.解：∴126PFPF∵焦点为12(5,0),(5,0)FF∴可设双曲线方程为:22221xyab(a>0,b>0).∵2a=6,2c=10,∴a=3,c=5.∴b2=52－32=16.所以点P的轨迹方程为221916xy(3)≥x.∵1210FF>6,由双曲线的定义可知，点P的轨迹是双曲线的一支课本例2(右支),使A、B两点在x轴上，并且点O与线段AB的中点重合解:由声速及在A地听到炮弹爆炸声比在B地晚2s,可知A地与爆炸点的距离比B地与爆炸点的距离远680m.因为AB>680m,所以爆炸点的轨迹是以A、B为焦点的双曲线在靠近B处的一支上.例3.(课本第54页例)已知A,B两地相距800m,在A地听到炮弹爆炸声比在B地晚2s,且声速为340m/s,求炮弹爆炸点的轨迹方程.如图所示，建立直角坐标系xOy,设爆炸点P的坐标为(x,y)，则3402680PAPB即2a=680，a=340800AB8006800,0PAPBx1(0)11560044400xyx222800,400,ccxyoPBA因此炮弹爆炸点的轨迹方程为44400bca222思考1:若在A,B两地同时听到炮弹爆炸声,则炮弹爆炸点的轨迹是什么?思考2:根据两个不同的观测点测得同一炮弹爆炸声的时间差，可以确定爆炸点在某条曲线上，但不能确定爆炸点的准确位置.而现实生活中为了安全，我们最关心的是炮弹爆炸点的准确位置，怎样才能确定爆炸点的准确位置呢?答:爆炸点的轨迹是线段AB的垂直平分线.答:再增设一个观测点C，利用B、C（或A、C）两处测得的爆炸声的时间差，可以求出另一个双曲线的方程，解这两个方程组成的方程组，就能确定爆炸点的准确位置.这是双曲线的一个重要应用.例2:如果方程表示双曲线，求m的取值范围.22121xymm解:方程可以表示方程可以表示哪些曲线？哪些曲线？_____________._____________.22121xymm思考：21mm得或(2)(1)0mm由∴m的取值范围为(,2)(1,)题型三双曲线定义的应用设P为双曲线x2－y212＝1上的一点，F1，F2是该双曲线的两个焦点，若PF1∶PF2＝3∶2，求△PF1F2的面积．例3【解】已知得2a＝2，又由双曲线的定义得PF1－PF2＝2，∵PF1∶PF2＝3∶2，∴PF1＝6，PF2＝4.又F1F2＝2c＝213，由余弦定理，得cos∠F1PF2＝62＋42－522×6×4＝0，∴三角形F1PF2为直角三角形．S△PF1F2＝12×6×4＝12.【名师点评】双曲线的定义是解决与双曲线有关的问题的主要依据，在应用时，一是注意条件PF1－PF2＝2a(0<2a