《双曲线的简单几何性质》人教版高中数学选修2-1PPT课件（第2.3.2课时）.pptx

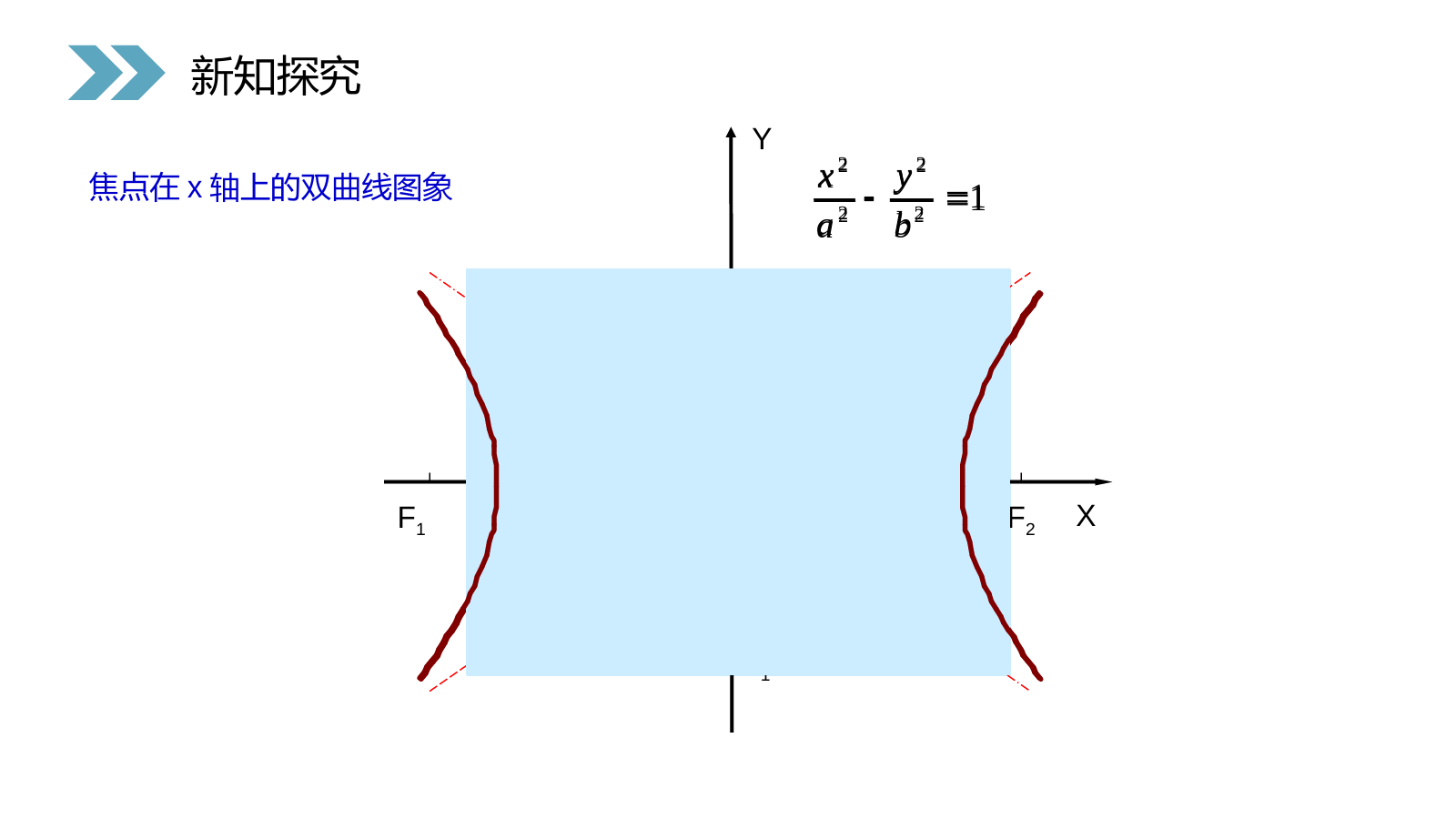
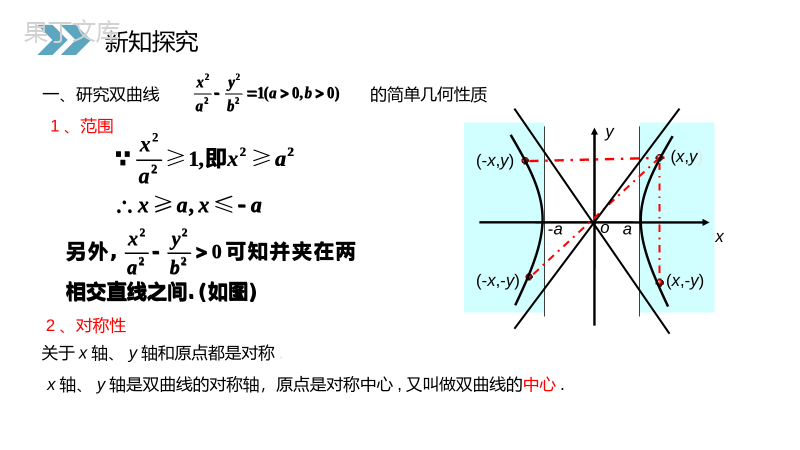
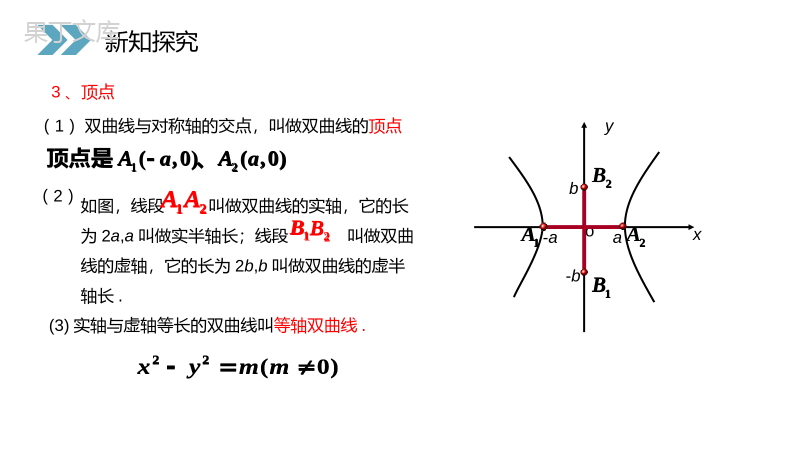
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-12.3.2双曲线的简单几何性质第2章圆锥曲线与方程人教版高中数学选修2-1双曲线的标准方程:)0,0(12222babyax形式一：（焦点在x轴上，（-c，0）、（c，0））1F2F形式二：（焦点在y轴上，（0，-c）、（0，c））其中)0,0(12222babxay1F2F222bac双曲线的图象特点与几何性质?现在就用方程来探究一下!类似于椭圆几何性质的研究.复习回顾)0,0(12222babyax1F2F)0,0(12222babxay1F2F222bacYXF1F2A1A2B1B212222byax焦点在x轴上的双曲线图象新知探究12222byax2、对称性一、研究双曲线的简单几何性质1、范围22221,,≥≥≥≤xxaaxaxa即关于x轴、y轴和原点都是对称.x轴、y轴是双曲线的对称轴，原点是对称中心,又叫做双曲线的中心.xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)22221(0,0)xyabab另外,22220xyab可知并夹在两相交直线之间.(如图)新知探究22221,,≥≥≥≤xxaaxaxa即22221(0,0)xyabab另外,22220xyab可知并夹在两相交直线之间.(如图)3、顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点xyo-b1B2Bb1A2A-aa如图，线段叫做双曲线的实轴，它的长为2a,a叫做实半轴长；线段叫做双曲线的虚轴，它的长为2b,b叫做双曲线的虚半轴长.2A1A2B1B（2）(3)实轴与虚轴等长的双曲线叫等轴双曲线.22(0)xymm顶点是12(,0)(,0)AaAa、新知探究1B2B1A2A2A1A2B1B22(0)xymm顶点是12(,0)(,0)AaAa、4、渐近线1A2A1B2Bxyobyxabyxaab利用渐近线可以较准确的画出双曲线的草图(2)渐近线对双曲线的开口的影响(3)双曲线上的点与这两直线有什么位置关系呢?⑴双曲线22221xyab(0,0)ab的渐近线为byxa注:等轴双曲线22(0)xymm的渐近线为yx如何记忆双曲线的渐近线方程？新知探究1A2A1B2Bbyxabyxa⑴双曲线22221xyab(0,0)ab的渐近线为byxa注:等轴双曲线22(0)xymm的渐近线为yx5、离心率e是表示双曲线开口大小的一个量,e越大开口越大⑵e的范围:c>a>0e>1⑶e的含义:2222()11bcaceaaa∴当(1,)e时,(0,)ba,且e增大,ba也增大.e增大时,渐近线与实轴的夹角增大.另外（4）等轴双曲线的离心率e=?2,反过来也成立.∵222,ceabca新知探究⑴定义:双曲线的焦距与实轴长的比,叫做双曲线的离心率.同样可以形象地理解焦点离开中心的程度.⑸在四个参数中,知二求二.⑵e的范围:⑶e的含义:2222()11bcaceaaa∴当(1,)e时,(0,)ba,且e增大,ba也增大.e增大时,渐近线与实轴的夹角增大.另外2,反过来也成立.∵222,ceabcaXYF1F2OB1B2A2A112222bxay焦点在y轴上的双曲线图像新知探究12222bxay焦点在y轴上的双曲线的几何性质口答双曲线标准方程：YX12222bxay0byax双曲线性质：1、范围：y≥a或y≤-a2、对称性：关于x轴，y轴，原点对称。3、顶点B1（0，-a），B2（0，a）4、轴：实轴B1B2;虚轴A1A2A1A2B1B25、渐近线方程：6、离心率：e=c/aF2F2o如何记忆双曲线的渐进线方程？新知探究12222bxay0byax小结ax或axayay或)0,(a),0(axabyxbayace)(222bac其中关于坐标轴和原点都对称性质双曲线)0,0(12222babyax)0,0(12222babxay范围对称性顶点渐近线离心率图象新知探究axaxayay)0,(a),0(axabyxbayace)(222bac其中)0,0(12222babyax)0,0(12222babxay例1求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐进线方程.可得实半轴长a=4，虚半轴长b=3焦点坐标为（0，-5）、（0，5）45ace离心率xy34渐进线方程为解：把方程化为标准方程221169yx课堂练习45ace离心率xy34渐进线方程为221169yx变式训练1.如果直线y＝kx－1与双曲线x2－y2＝4没有公共点，求k的取值范围．解：由y＝kx－1x2－y2＝4得(1－k2)x2＋2kx－5＝0，易知此方程无解．由1－k2≠0Δ＝4k2＋20（1－k2）<0得k>52或k<－52，则k的取值范围为k>52或k<－52.课堂练习解：由y＝kx－1x2－y2＝4得(1－k2)x2＋2kx－5＝0，易知此方程无解．由1－k2≠0Δ＝4k2＋20（1－k2）<0得k>52或k<－52，则k的取值范围为k>52或k<－52.1．若直线y＝kx－1与双曲线x2－y2＝1有且只有一个交点，则k的值为________．解析：由y＝kx－1，x2－y2＝1，得(1－k2)x2＋2kx－2＝0.当1－k2＝0时，即k＝±1时，方程变为±2x－2＝0，则x＝±1.此时直线与双曲线渐近线平行，有且只有一个交点．课堂练习当1－k2≠0时，Δ＝4k2＋8(1－k2)＝0，解得k＝±2.此时直线与双曲线相切，有且只有一个公共点．综上所述,k＝±1，±2.答案：±1,±2解析：由y＝kx－1，x2－y2＝1，得(1－k2)x2＋2kx－2＝0.当1－k2＝0时，即k＝±1时，方程变为±2x－2＝0，则x＝±1.此时直线与双曲线渐近线平行，有且只有一个交点．当1－k2≠0时，Δ＝4k2＋8(1－k2)＝0，解得k＝±2.此时直线与双曲线相切，有且只有一个公共点．综上所述,k＝±1，±2.答案：±1,±22．过点P(8,1)的直线与双曲线x2－4y2＝4相交于A,B两点，且P是线段AB的中点，求直线AB的方程．解：设A,B的坐标分别为(x1，y1),(x2，y2)，则x21－4y21＝4，①x22－4y22＝4.②①－②得(x1＋x2)(x1－x2)－4(y1＋y2)(y1－y2)＝0.课堂练习∵P是线段AB的中点，∴x1＋x2＝16，y1＋y2＝2.∴y1－y2x1－x2＝x1＋x24y1＋y2＝2.∴直线AB的斜率为2.∴直线AB的方程为y－1＝2(x－8)，即2x－y－15＝0.解：设A,B的坐标分别为(x1，y1),(x2，y2)，则x21－4y21＝4，①x22－4y22＝4.②①－②得(x1＋x2)(x1－x2)－4(y1＋y2)(y1－y2)＝0.∵P是线段AB的中点，∴x1＋x2＝16，y1＋y2＝2.∴y1－y2x1－x2＝x1＋x24y1＋y2＝2.∴直线AB的斜率为2.∴直线AB的方程为y－1＝2(x－8)，即2x－y－15＝0.关于x轴、y轴、原点对称图形方程范围对称性顶点离心率1(0)xyabab2222A1（-a，0），A2（a，0）A1（0，-a），A2（0，a）100yx(a,b)ab2222≥≤yayaxR，或关于x轴、y轴、原点对称(1)ceea渐进线ayxb..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c)≥≤xaxayR，或(1)ceeabyxa小结1(0)xyabab2222100yx(a,b)ab2222≥≤yayaxR，或(1)ceeaayxb≥≤xaxayR，或(1)ceeabyxa椭圆双曲线方程abc关系图象12=+byax222（a＞b＞0）12222=-byax(a＞0b＞0)222=+ba(a＞0b＞0)c222=-ba(a＞b＞0)cyXF10F2MXY0F1F2p小结椭圆与双曲线的性质比较感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明渐近线离心率顶点对称性范围准线xa,y≤bx≥a，yR对称轴：x轴，y轴对称中心：原点对称轴：x轴，y轴对称中心：原点（-a,0)(a,0)(0,b)(0,-b)长轴：2a短轴：2b(-a,0)(a,0)实轴：2a虚轴：2be=ac(0＜e＜1)ace=(e＜1)无y=abx±cax2cax2小结cax2cax2讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第2章圆锥曲线与方程人教版高中数学选修2-1