有理数的混合运算(课件)-2022-2023学年七年级数学上册教材配套教学课件+分层练习(人教版)

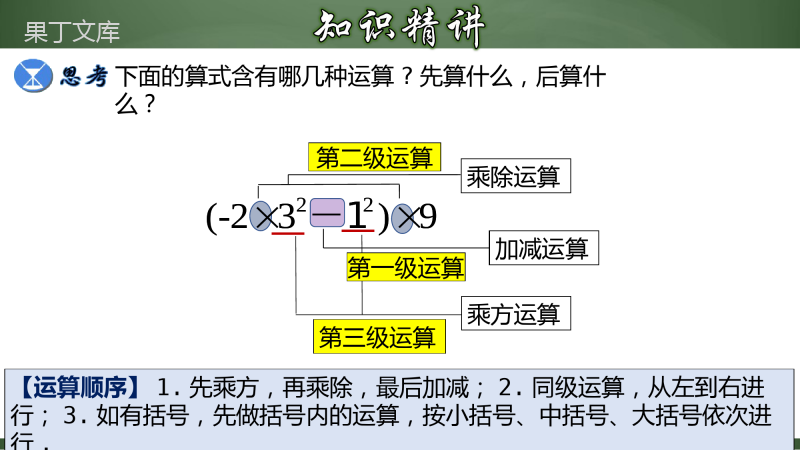
有理数的混合运算1.进一步掌握有理数的运算法则和运算律.2.熟练地按有理数运算顺序进行混和运算.(重点、难点）乘方的符号法则：（1）正数的任何次幂都是正数；（2）负数的奇次幂是负数，负数的偶次幂是正数；（3）零的正整数次幂都是零.求n个相同因数的积的运算叫做乘方，乘方的结果叫做幂.na组成要素幂指数底数因数因数的个数乘方的定义na下面的算式含有哪几种运算?先算什么，后算什么？22(-23)9－1加减运算第三级运算乘除运算第二级运算乘方运算第一级运算【运算顺序】1.先乘方，再乘除，最后加减；2.同级运算，从左到右进行；3.如有括号，先做括号内的运算，按小括号、中括号、大括号依次进22(-23)9－1例3.计算：(1)2×(-3)3-4×(-3)+15(2)(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)上述两个式子中，存在着哪几种运算？你认为应按怎样的顺序计算？解：(1)原式=2×(-27)-(-12)+15=-54+12+15=-27(2)原式=-8+(-3)×(16+2)-9÷(-2)=-8+(-3)×18-(-4.5)=-8-54+4.5=-57.5计算：(1)(-1)10×2+(-2)3÷4(2)(-5)3-3×(-)4(3)×(-)×÷(4)(-10)4+[(-4)2-(3+32)×2]解：(1)原式=1×2+(-8)÷4=2+(-2)=0(2)原式=-125-3×=-125-=-125(3)原式=×(-)××=-(4)原式=10000+[16-(3+9)×2]=10000+(16-12×2)=10000+(16-24)=10000+(-8)=9992例2.观察下面三行数：-2，4，-8，16，-32，64，…；①0，6，-6，18，-30，66，…；②-1，2，-4，8，-16，32，….③（1）第①行数按什么规律排列？解：（1）第①行数是-2，(-2)2，(-2)3，(-2)4，…分析：观察①，发现各数均为2的倍数.联系数的乘方，从符号和绝对值两方面考虑，可发现排列的规律.解:(2)对比①②两行中位置相对应的数，可以发现：第②行数是第①行相应的数加2，即-2+2，(-2)2+2，(-2)3+2，(-2)4+2，…对比①③两行中位置相对应的数，可以发现：第③行数是第①行相应的数的0.5倍，即-2×0.5，(-2)2×0.5，(-2)3×0.5，(-2)4×0.5，…例2.观察下面三行数：-2，4，-8，16，-32，64，…；①0，6，-6，18，-30，66，…；②-1，2，-4，8，-16，32，….③（2）第②③行数与第①行数分别有什么关系？解：（3）每行数中的第10个数的和是(-2)10+[(-2)10+2]+(-2)10×0.5=1024+(1024+2)+1024×0.5=1024+1026+512=2562例2.观察下面三行数：-2，4，-8，16，-32，64，…；①0，6，-6，18，-30，66，…；②-1，2，-4，8，-16，32，….③（3）取每行数的第10个数，计算这三个数的和.(1)计算:2-1=___;2①②2-2-1=___;2③3-22-2-1=___;2④4-23-22-2-1=___;2⑤5-24-23-22-2-1=___.(2)根据上面的计算结果猜想:22020-22019-22018-…-22-2-1的值为____;2n-2n-l-2n-2-.….-22-2-1的值为____.(3)根据上面猜想的结论，求213-212-211-210-29-28-27-26的值.1111111解:由猜想的结论得:213-212-211-210-29-28-27-26-25-24-23-22-2-1=1所以，213-212-211-210-29-28-27-26=1+1+2+22+23+24+25=1+2+4+8+16+321.在(-1)3，(-1)2，-22，(-3)2，这4个数中，最大的数与最小的数和等于()A.6B.8C.-5D.52.若0