九年级数学上册--相似形复习课件

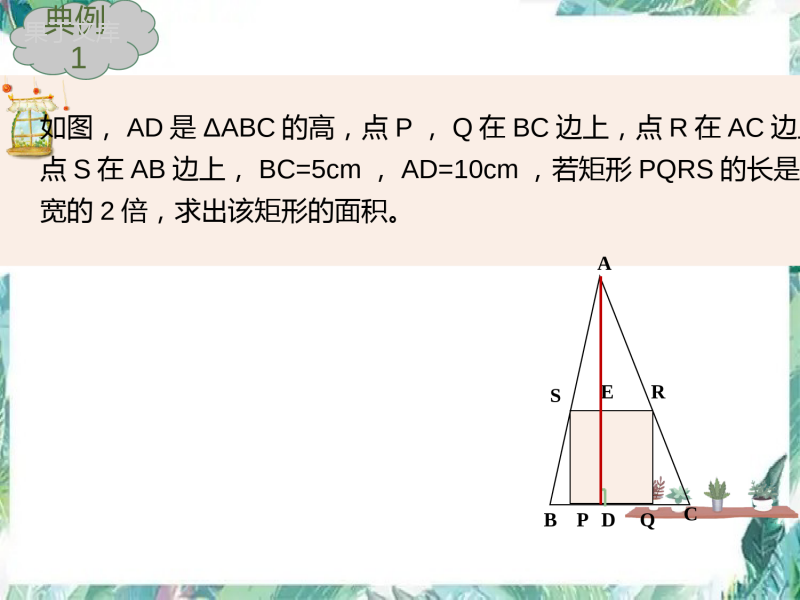
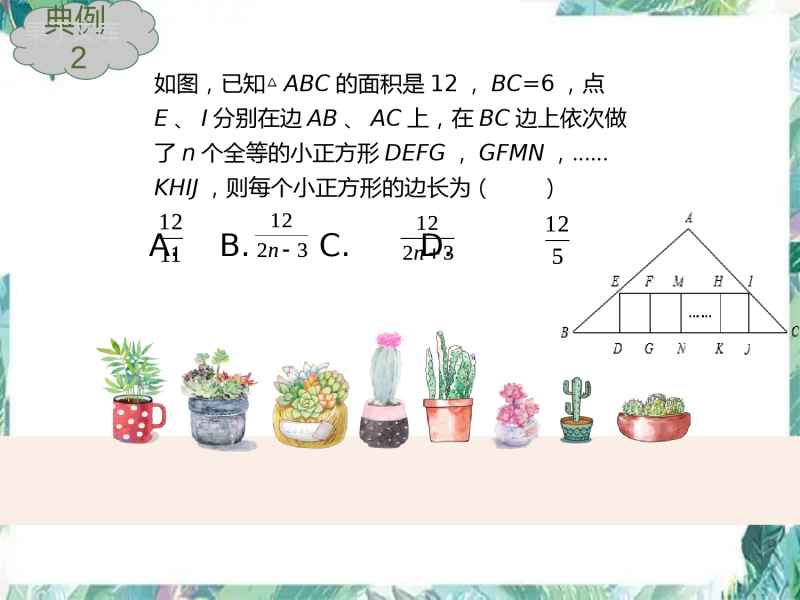
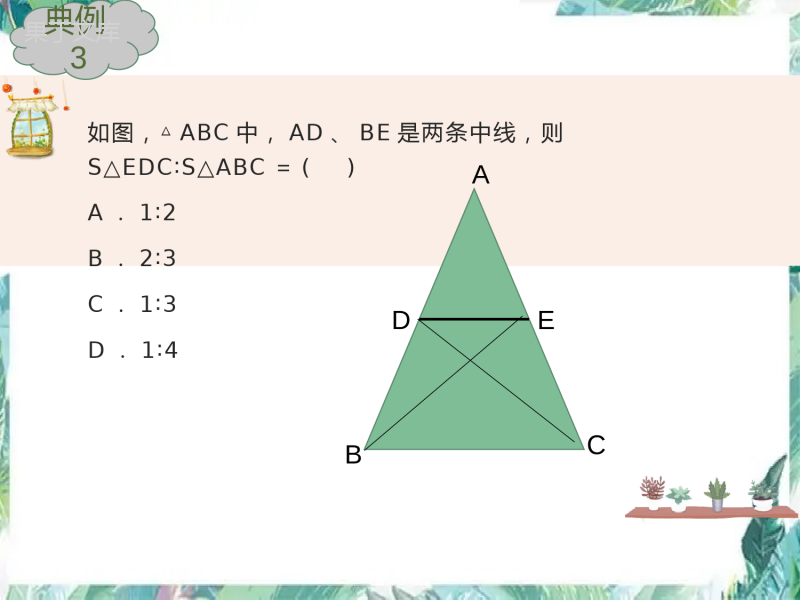
相似形复习课3一.相似三角形的性质性质1.相似三角形对应高的比、对应角平分线的比、对应中线的比都等于相似比．性质2.相似三角形周长的比等于相似比.性质3.相似三角形的面积比等于相似比的平方.如图，AD是ΔABC的高，点P，Q在BC边上，点R在AC边上点S在AB边上，BC=5cm，AD=10cm，若矩形PQRS的长是宽的2倍，求出该矩形的面积。SRQPEDCBA典例1如图，已知△ABC的面积是12，BC=6，点E、I分别在边AB、AC上，在BC边上依次做了n个全等的小正方形DEFG，GFMN，……KHIJ，则每个小正方形的边长为（）A.B.C.D.11123212n3212n512典例211123212n3212n512如图，△ABC中，AD、BE是两条中线，则S△EDC∶S△ABC＝()A．1∶2B．2∶3C．1∶3D．1∶4ABCDE典例3如图，在△ABC中，EF∥BC，，S梯形BCFE＝8，则S△ABC是_________.21EBAEEFBCA典例421EBAE将△ABC沿BC方向平移得到△DEF，△ABC与△DEF重叠部的面积是△ABC的面积的一半.已知BC=2，求△ABC平移的距离.ADBECF典例5如图，△ABC中，DEBC∥，DE分别交AB、AC于点D、E，S△ADE＝2S△DCE，求S△ADE∶S△ABC.ABCDE典例6二.位似图形概念：1.是相似图形2.对应点的连线相交于一点性质：1.位似是特殊的相似，具有相似图形的所有性质2.对应点的连线相交于同一点3.位似图形的对应线段平行或者在一条直线上相关概念：1.位似比：对应点到位似中心连线的长度比，也是相似比2.位似中心：对应点连线相交于同一点，该点即为位似中心下列说法：①位似图形一定是相似图形；②相似图形一定是位似图形；③两个位似图形若全等，则位似中心在两个图形之间；④若五边形ABCDE与五边形A′B′C′D′E′位似，则其中△ABC与△A′B′C′也是位似的，且位似比相等.其中正确的有.典例1在如图所示的四个图形中，位似图形的个数为()A.1个B.2个C.3个D.4个C典例2如图，五边形ABCDE与五边形A′B′C′D′E′是位似图形，且位似比为，若五边形ABCDE的面积为18cm2，周长为21cm，那么五边形A′B′C′D′E′的面积为（）cm2，周长为（）cm．23典例323画位似图形的方法：根据位似比，找到对应点的位置，顺次连接即可得到位似图形2.连接位似中心和图形上的关键点（一般为各个顶点），正向延长或反向延长所在直线1.确定位似中心，可以在图形里面，也可以在图形外面，还可以在图形上如图，作△ABC的位似图形△DEF，使其与△ABC位似，且位似比为2（用多种方法作图）.ACB典例三.平面直角坐标系中的位似变换以原点为位似中心，作位似图形，有2种方法，一个是在原点的同一侧，一个是在原点两侧知识点1：知识点2：如果位似图形在原图的同一侧，则对应点的横，纵坐标比为位似比k如果位似图形在原图的异侧，则对应点的横，纵坐标比为-k将如图各点纵坐标不变，横坐标乘以2，所得图形与原图形比（）A．形状大小变了，整体鱼被横向拉长为原来的2倍B．形状大小变了，整体鱼被纵向拉长为原来的2倍C．形状大小不变，整体鱼向右移动了两个单位D．形状大小不变，整体鱼向左移动了两个单位典例4在平面直角坐标系中，点A，B的坐标分别为(－6，3)，(－12，9)，△ABO和△A′B′O是以原点O为位似中心的位似图形.若点A′的坐标为(2，－1),则点B′的坐为.典例5如图，正方形ABCD和正方形OEFG中，点A和点F的坐标分别为(3，2)，(－1，－1)，则两个正方形的位似中心的坐标是___________________．(1，0)或(－5，－2)yxADOBCFGE典例6位似图形的平面直角坐标系作图题是非常重要的，中考的热门考点，因为ppt不好操作，所以老师把题目整理成纸质版，大家一起练习。付出就有收获解释说明