第二十三章+旋转(章末小结)(课件)-2022-2023学年九年级数学上册同步精品课堂(人教版)

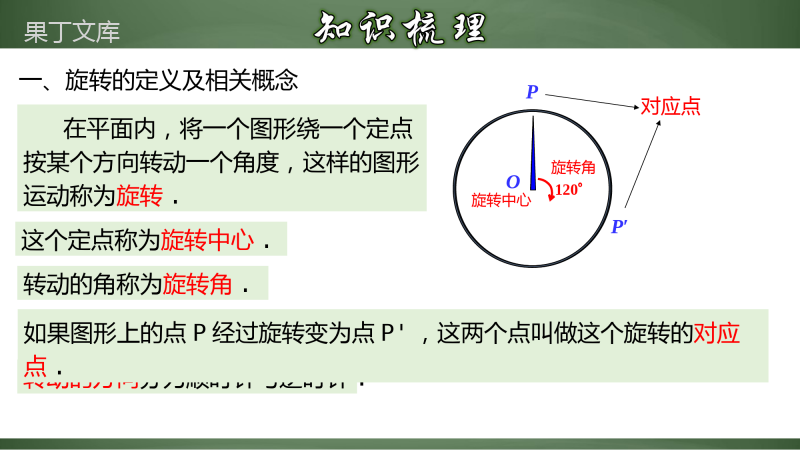
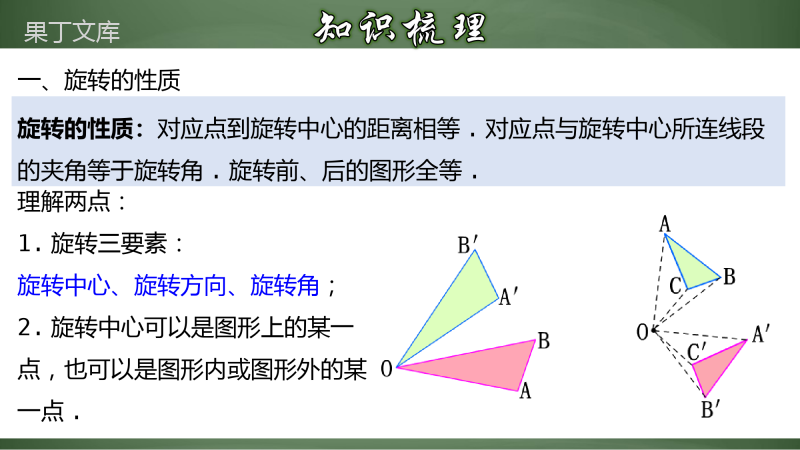
旋转章末小结1.梳理本章的知识要点，回顾与复习本章知识;2.进一步明确旋转、中心对称、中心对称图形的概念及性质,并会作图;(重、难点)3.能熟练说出一个点关于原点对称的坐标;(重点)4.能灵活应用平移、旋转、轴对称变换进行图案设计,体会数学的美感.(难点)在平面内，将一个图形绕一个定点按某个方向转动一个角度，这样的图形运动称为旋转.120OP′P旋转中心旋转角对应点一、旋转的定义及相关概念这个定点称为旋转中心.转动的角称为旋转角.转动的方向分为顺时针与逆时针.如果图形上的点P经过旋转变为点P'，这两个点叫做这个旋转的对应点.旋转的性质：对应点到旋转中心的距离相等.对应点与旋转中心所连线段的夹角等于旋转角.旋转前、后的图形全等.理解两点：1.旋转三要素：旋转中心、旋转方向、旋转角；2.旋转中心可以是图形上的某一点，也可以是图形内或图形外的某一点.一、旋转的性质三、旋转作图的条件：(1)有原图形(2)有旋转中心(3)有旋转方向(4)有旋转角四、旋转作图的步骤：(1)确定图形的关键点；(2)作出旋转后的对应点；(3)顺次连线即可.五、中心对称的定义像这样，把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，这个点叫做对称中心，(简称中心).这两个图形在旋转后能重合的对应点叫做关于对称中心的对称点.轴对称中心对称1有一条对称轴——直线有一个对称中心——点2图形沿轴对折（翻转180°）图形绕中心旋转180°3翻转后和另一个图形重合旋转后和另一个图形重合1ABCC1AB1O六、中心对称与轴对称的异同像这样，把一个图形绕着某一个点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心.中心对称图形的性质：中心对称图形上对应点的连线都经过对称中心，且被对称中心平分.七、中心对称图形及其性质两个点关于原点对称时，它们的坐标符号相反，即点P(x，y)关于原点的对称点为P′(-x，-y).作关于原点对称的图形的一般步骤：(1)写出各点关于原点对称的点的坐标；(2)在坐标平面内描出这些对称点；(3)参照原图形顺次连接各点，即为所求作的对称图形.八、关于原点对称的点的坐标旋转的性质及应用1例1.以原点为中心,将点P(4,5)按逆时针方向旋转90°，得到的点Q所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限B例2.如图，在△ABC中，∠ACB＝90°，将△ABC绕点C顺时针旋转得到△DEC，使点B的对应点E恰好落在边AC上，点A的对应点为D，延长DE交AB于点F，则下列结论一定正确的是()A．AC＝DEB．BC＝EFC．∠AEF＝∠DD．AB⊥DF旋转的性质及应用1D例3.如图，△ABC中，∠ACB＝90°，∠ABC＝40°.将△ABC绕点B逆时针旋转得到△A′BC′，使点C的对应点C′恰好落在边AB上，则∠CAA′的度数是()A．50°B．70°C．110°D．120°D旋转的性质及应用1例4.如图，在平面直角坐标系中，将边长为1的正方形OABC绕点O顺时针旋转后得到正方形，依此方式，绕点O连续旋转2021次得到正方形，那么点的坐标是（）A．B．C．D．D旋转的性质及应用1【1-1】如图，在△ABC中，，，将三角形ABC绕点A按顺时针方向旋转到三角形的位置，使得点C，A，在一条直线上，那么旋转角等于（）A．50°B．80°C．100°D．130°D【1-2】如图，将Rt△ABC的斜边AB绕点A顺时针旋转α(0°＜α＜90°)得到AE，直角边AC绕点A逆时针旋转β(0°＜β＜90°)得到AF，连接EF.若AB＝3，AC＝2，且α＋β＝∠B，则EF＝______．√??【1-3】如图，平面直角坐标系中，已知△ABC的顶点A的坐标为(-1,2).(1)将△ABC向右平移3个单位得到△DEF，请在图中画出平移后的图形;(2)将△ABC绕点C按逆时针方向旋转90°后得到△MNC,请在图中画出旋转后的图形，并写出点M，N的坐标.解:(1)如图，△DEF为所作;(2)如图，△MNC为所作，M(-3,-2),N(-2，-4).中心对称图形典型应用2例5.下列四个高校校徽主体图案是中心对称图形的是（）【分析】本题考查识别中心对称图形．掌握使图形绕某一点旋转180°后与原来的图形重合的图形是中心对称图形是解题关键．A．是中心对称图形，符合题意；B．不是中心对称图形，不符合题意；C．不是中心对称图形，不符合题意；D．不是中心对称图形，不符合题意．A中心对称图形典型应用2例6.如图，在平面直角坐标系中，△ABC顶点的横、纵坐标都是整数．若将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF，其中A、B、C分别和D、E、F对应，则旋转中心的坐标是（）A.（0，0）B.(1,0)C.(1,-1)D.(0.5,0.5)C【分析】根据对应点连接线段的垂直平分线的交点即为旋转中心，作出旋转中心，可得结论；如图，点Q即为所求，Q(1,-1)；例7.如图，平面直角坐标系中，△OA1B1是边长为2的等边三角形，作△B2A2B1与△OA1B1关于点B1成中心对称，再作△B2A3B3与△B2A2B1于点B2成中心对称，如此作下去，则△B2020A2021B2021的顶点A2021的坐标是___________.【分析】首先根据△OA1B1是边长为2的等边三角形，可得A1的坐标为(1，)，B1的坐标为(2，0)；然后根据中心对称的性质，分别求出点A2、A3、A4的坐标各是多少；最后总结出An的坐标的规律，求出A2021的坐标是多少(4041,√3)中心对称图形典型应用2【2-1】下列所述图形中，既是轴对称图形又是中心对称图形的是()A．等腰三角形B．等边三角形C．菱形D．平行四边形【2-2】图是由8个大小相等的正方形组成的中心对称图形，则此图的对称中心是（）A．点B．点C．点D．点CA【2-3】如图是两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心按逆时针方向进行旋转，第一次旋转后得到图①，第二次旋转后得到图②，…，则第次旋转后得到的图形与图①-④中相同的是（）A．图①B．图②C．图③D．图④B关于原点对称的点的坐标3例8.若点P(m，－m＋3)关于原点的对称点Q在第三象限，则m的取值范围是()A．0＜m＜3B．m＜0C．m＞0D．m≥0A例9.平面直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.关于原点对称的点的坐标3解:根据题意,得x2+2x+x+2=0,y=-3∴x1=-1,x2=-2,y=-3∵x2+2x＜0,∴x=-1∴x+2y=-7.例10.如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点上，点A的坐标是（1，-4）．(1)作出△ABC关于原点O对称的△A1B1C1；(2)将△A1B1C1向右平移5个单位长度，得到△A2B2C2，画出△A2B2C2；(3)如果△ABC可以通过一次旋转得到△A2B2C2，则旋转中心的坐标是．关于原点对称的点的坐标3例10.如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点上，点A的坐标是（1，-4）．(1)作出△ABC关于原点O对称的△A1B1C1；(1)解：∵由图可知：A(2,-2),B(1,-4),C(4,-3),∴A1(-2,2),B1(-1,4),C1(-4,3),如图所示：△A1B1C1，即为所求；关于原点对称的点的坐标3例10.如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点上，点A的坐标是（1，-4）．(2)将△A1B1C1向右平移5个单位长度，得到△A2B2C2，画出△A2B2C2；(2)解：∵由图可知：A1(-2,2),B1(-1,4),C1(-4,3),∴将△A1B1C1向右平移5个单位长度，得到A2(3,2),B2(4,4),C2(1,3),如图所示：△A2B2C2，即为所求；关于原点对称的点的坐标3例10.如图，在每个小正方形的边长为1个单位的网格中，△ABC的顶点均在格点上，点A的坐标是（1，-4）．(3)如果△ABC可以通过一次旋转得到△A2B2C2，则旋转中心的坐标是．(3)解：如图连接AA2,CC2，线段AA2与线段CC2交点即为所求，旋转中心坐标为（2.5,0）关于原点对称的点的坐标3【3-1】己知点P1(a,-3)和P2(-4,b)关于x轴对称，则(a+b)2000的值为()A.1B.-1C.72000D.-72000【3-2】已知点P的坐标为(2-a,3a+6)，且点P到两坐标轴的距离相等，则点P关于原点0对称点的坐标为()A.(-3，3)B.(-3，-3)C.(-6，6)D.(-3，-3)或(-6，6)AD【3-3】如图，在平面直角坐标系中，已知ABC的三个顶点坐标分别是A(1，1)，B(4，1)，C(3，3)(1)画出ABC关于原点O的中心对称图形；(2)若点P为y轴上一动点，则PA+PC的最小值为______．解：（1）如图，即为所求，（2）作点A关于y轴对称点，连接C交y轴于点P，此时PA+PC的值最小，如上图，由图像可得最小值=C=，利用旋转进行证明或计算4例11.如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为H，与BC交于点G.若BG＝3，CG＝2，则CE的长为()A.B.C．4D.【分析】如图，连接EG.由旋转可得△ADE≌△ABF，∴AE＝AF，DE＝BF.又∵AG⊥EF，∴H为EF的中点．∴AG垂直平分EF.∴EG＝FG.设CE＝x，则DE＝5－x＝BF，FG＝BF＋BG＝8－x，∴EG＝8－x.∵在Rt△CEG中，∠C＝90°，∴CE2＋CG2＝EG2，即x2＋22＝(8－x)2.解得x＝.∴CE的长为.故选B.利用旋转进行证明或计算4例11.如图，点E在正方形ABCD的边CD上，将△ADE绕点A顺时针旋转90°到△ABF的位置，连接EF，过点A作EF的垂线，垂足为H，与BC交于点G.若BG＝3，CG＝2，则CE的长为()A.B.C．4D.B例12.如图,在四边形ABCD中，∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.(1)求证:AE⊥BD;利用旋转进行证明或计算4(1)证明:由旋转可得AC=BC∵∠ABC=45°,∴∠BCA=90°.设BD与AC、AE分别交于点M、N,如图所示.:∠AMN=∠BMC,∠CAE=∠CBD,例12.如图,在四边形ABCD中，∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.(2)若AD=2,CD=3,试求四边形ABCD的对角线BD的长.利用旋转进行证明或计算4(2)解:如图，连接DE.由旋转可得AE=BD,CE=CD,∠DCE=∠ACB=90°∵CD=CE=3,∴DE=3,∠CDE=45°∴∠ADE=∠ADC+∠CDE=90°∴AE==∴BD=.利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(1)探究线段MD、MF的位置及数量关系，直接写出答案即可；(2)将正方形CGEF绕点C逆时针旋转45°（如图乙），令CG＝2BC其他条件不变，结论是否发生变化，并加以证明；(3)将正方形CGEF绕点C旋转任意角度后（如图丙），其他条件不变．探究：线段MD，MF的位置及数量关系，并加以证明．利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(1)探究线段MD、MF的位置及数量关系，直接写出答案即可；关系：MD＝MF，MD⊥MF证明：如图，延长DM交CE于点N，连接FD、FN∵正方形ABCD，∴ADBE，AD＝DC，∴∠1＝∠2又∵AM＝EM，∠3＝∠4∴△ADM≌△ENM∴AD＝EN，MD＝MN∵AD＝DC，∴DC＝NE，利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(1)探究线段MD、MF的位置及数量关系，直接写出答案即可；又∵正方形CGEF，∴∠FCE＝∠NEF＝45°，FC＝FE，∠CFE＝90°又∵正方形ABCD，∴∠BCD＝90°．∴∠DCF＝∠NEF＝45°∴△FDC≌△FNE∴FD＝FN，∠5＝∠6∵∠CFE＝90°，∴∠DFN＝90°又∵DM＝MN＝DN，∴M为DN的中点，∴FM＝DN，∴MD＝MF，DM⊥MF．利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(2)将正方形CGEF绕点C逆时针旋转45°（如图乙），令CG＝2BC其他条件不变，结论是否发生变化，并加以证明；结论不变MD＝MF，MD⊥MF，证明：如图，延长DM交FE于N．∵正方形ABCD、CGEF，∴CF＝EF，AD＝DC，∠CFE＝90°，ADFE，∴∠1＝∠2．在△AMD与△EMN中，∵，利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(2)将正方形CGEF绕点C逆时针旋转45°（如图乙），令CG＝2BC其他条件不变，结论是否发生变化，并加以证明；∴△AMD≌△EMN，∴AD＝EN，MD＝MN，∵CG＝2BC∴CF＝2CD=2AD，EF＝CF=2AD=2EN，∴FD＝FN．又∵∠DFN＝90°，∴FM⊥MD，MF＝MD；利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(3)将正方形CGEF绕点C旋转任意角度后（如图丙），其他条件不变．探究：线段MD，MF的位置及数量关系，并加以证明．MD＝MF，MD⊥MF，证明：如图，延长DM到N，使MN＝MD，连接FD、FN、EN，延长EN与DC延长线交于点H．在△AMD与△EMN中，∵，∴△AMD≌△EMN，∴∠3＝∠4，AD＝NE．利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(3)将正方形CGEF绕点C旋转任意角度后（如图丙），其他条件不变．探究：线段MD，MF的位置及数量关系，并加以证明．又∵正方形ABCD、CGEF，∴CF＝EF，AD＝DC，∠ADC＝90°，∠CFE＝∠ADC＝∠FEG＝∠FCG＝90°．∴DC＝NE．∵∠3＝∠4，∴ADEH．∴∠H＝∠ADC＝90°．∵∠G＝90°，∠5＝∠6，∴∠7＝∠8．利用旋转进行证明或计算4例13.如图甲，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上（CG＞BC），取线段AE的中点M．(3)将正方形CGEF绕点C旋转任意角度后（如图丙），其他条件不变．探究：线段MD，MF的位置及数量关系，并加以证明．∵∠7＋∠DCF＝∠8＋∠FEN＝90°，∴∠DCF＝∠FEN．在△DCF与△NEF中，∵，∴△DCF≌△NEF，∴FD＝FN，∠DFC＝∠NFE．∵∠CFE＝90°，∴∠DFN＝90°，∴FM⊥MD，MF＝MD．【4-1】如图，在四边形ABCD中，∠ABC＝30°，将△DCB绕点C顺时针旋转60°后，点D的对应点恰好与点A重合，得到△ACE.若AB＝3，BC＝4，则BD＝______(提示：可连接BE)．5【4-2】把直角三角形OAB与直角三角形O'CD如图1放置，直角顶点O与O′重合在一起，点D在OB上，∠B＝30°，∠C＝45°．现将△O'CD固定，△OAB绕点O顺时针旋转，旋转角α（0°≤α＜90°），OB与DC交于点E．(1)如图2，在旋转过程中，若OACD时，则α＝；若ABOC时，则α＝；(2)如图2，在旋转过程中，当△ODE有两个角相等时，α＝；(3)如图3，连结AC，在旋转过程中，猜想∠DOB与∠CAB＋∠ACD的大小关系，并说明理由．【4-2】把直角三角形OAB与直角三角形O'CD如图1放置，直角顶点O与O′重合在一起，点D在OB上，∠B＝30°，∠C＝45°．现将△O'CD固定，△OAB绕点O顺时针旋转，旋转角α（0°≤α＜90°），OB与DC交于点E．(1)如图2，在旋转过程中，若OACD时，则α＝；若ABOC时，则α＝；45°60°当OACD时当ABOC时【4-2】把直角三角形OAB与直角三角形O'CD如图1放置，直角顶点O与O′重合在一起，点D在OB上，∠B＝30°，∠C＝45°．现将△O'CD固定，△OAB绕点O顺时针旋转，旋转角α（0°≤α＜90°），OB与DC交于点E．(2)如图2，在旋转过程中，当△ODE有两个角相等时，α＝；当∠D＝∠DOE＝45°时，可得α＝∠DOE＝45°，当∠DOE＝∠DEO时，可得α＝∠DOE＝＝67.5°，故答案为：45°或67.5°；【4-2】把直角三角形OAB与直角三角形O'CD如图1放置，直角顶点O与O′重合在一起，点D在OB上，∠B＝30°，∠C＝45°．现将△O'CD固定，△OAB绕点O顺时针旋转，旋转角α（0°≤α＜90°），OB与DC交于点E．(3)如图3，连结AC，在旋转过程中，猜想∠DOB与∠CAB＋∠ACD的大小关系，并说明理由．如图3中，∠DOB与∠CAB+∠ACD的大小关系有三种情形：∠①DOB＞∠CAB+∠ACD．②∠DOB＝∠CAB+∠ACD．∠③DOB＜∠CAB+∠ACD．理由：∵∠1＝∠BAC+∠ACD，∠2＝∠D+∠1＝45°+∠1，∠3＝∠1+∠B＝30°+∠1，又∵∠BOD+∠2+∠3+（180°∠1﹣）＝360°，【4-2】把直角三角形OAB与直角三角形O'CD如图1放置，直角顶点O与O′重合在一起，点D在OB上，∠B＝30°，∠C＝45°．现将△O'CD固定，△OAB绕点O顺时针旋转，旋转角α（0°≤α＜90°），OB与DC交于点E．(3)如图3，连结AC，在旋转过程中，猜想∠DOB与∠CAB＋∠ACD的大小关系，并说明理由．∴∠BOD+45°+∠1+30°+∠1+180°∠1﹣＝360°，∴∠BOD+∠1＝105°，∴∠BOD+∠BAC+∠ACD＝105°，∴当0°≤∠DOB＜52.5°时，∠DOB＜∠CAB+∠ACD，当∠DOB＝52.5°中，∠DOB＝∠CAB+∠ACD，当52.5°＜∠DOB＜90°时，∠DOB＞∠CAB+∠ACD．