解直角三角形的应用(2)(课件)-2022-2023学年九年级数学下册同步精品课堂(人教版)

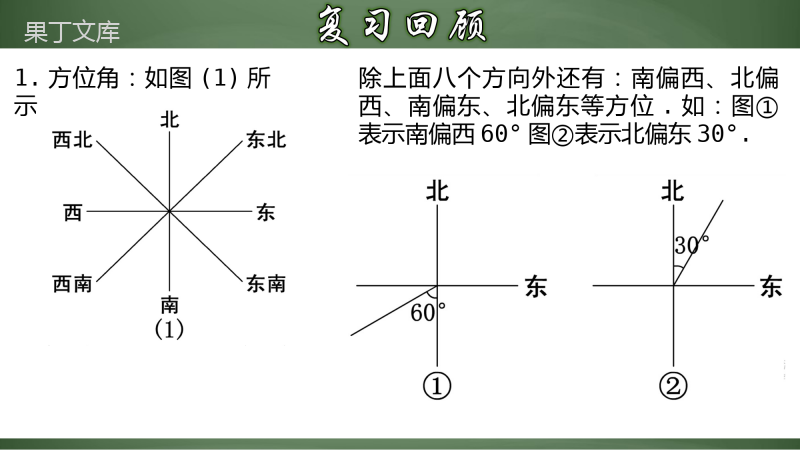
解直角三角形的应用(2)1.正确理解方向角、坡度的概念.(重点)2.能运用解直角三角形知识解决方向角、坡度的问题；能够掌握综合性较强的题型、融会贯通地运用相关的数学知识，进一步提高运用解直角三角形知识分析解决问题的综合能力.(重点、难点)1.方位角：如图(1)所示除上面八个方向外还有：南偏西、北偏西、南偏东、北偏东等方位.如：图①表示南偏西60°图②表示北偏东30°.例1.如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80nmile的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处，这时，海轮所在的B处距离灯塔P有多远（精确到0.01nmile）？解：如图，在Rt△APC中，PC=PA•cos(90°-65°)=80×cos25°≈72.505在Rt△BPC中，∠B=34°，∵sinB=∴PB==≈130(nmile)因此，当海轮到达位于灯塔P的南偏东34°方向时，它距离灯塔P大约130nmile.PCPBsinPCB7250534.sinPCPBsinPCB7250534.sin如图，海中有一个小岛A，它的周围8nmile内有暗礁，渔船跟踪鱼群由西向东航行，在B点测得小岛A在北偏东60°方向上，航行12nmile到达D点，这时测得小岛A在北偏东30°方向上.如果渔船不改变航线继续向东航行，有没有触礁的危险？解：作AC⊥BD.依题意得，∠ABD=30°，∠ADC=60°.∴∠BAD=∠ABD=30°∴AD=BD=12nmile∵sin60°=∴AC=AD·sin60°=12×=6∵6＞8∴渔船不改变航线继续向东航行，没有触礁的危险.ACAD32ACAD321.坡度：如图，坡面的垂直高度h与水平宽度a的比叫做坡度(坡比)，即i=.2.坡角：斜坡面与水平面的夹角α叫做坡角，l的长叫做坡面长.坡度与坡角的关系：tanα=i=.hahahaha例2.铁路路基横断面是一个等腰梯形，若腰的坡度是i=3:2，顶宽是3m，路基高是1.5m，求路基的下底宽？解：如图，AD=3m，作AE⊥BC，DF⊥BC.∵i=3:2，AE=DF=1.5m∴BE=CF=1m∴BC=1+1+3=5(m)即路基的下底宽为5m.如图，拦水坝的横断面为梯形ABCD，根据图中数据，求：(1)坡角α和β的度数；(2)斜坡AB的长(结果保留小数点后一位).解：(1)依题意得，tanα=，tanβ=∴α≈33.7°，β≈18.4°(2)∵i=1:1.5，AF=6m∴BF=1.5AF=1.5×6=9m由勾股定理得，(m)2313222296108.ABBFAF2313222296108.ABBFAF例3.已知：如图，斜坡AP的坡度为5：12，坡长AP为13米，在坡顶A处的同一水平面上有一颗大树BC，在斜坡底P处测得该树的树顶B的仰角为45°，在坡顶A处测得该树的树顶B的仰角为76°．求：(1)坡顶A到地面PQ的距离；(2)树BC的高度（结果精确到1米）.（参考数据：，，）(1)坡顶A到地面PQ的距离；（1）解：过点A作，垂足为点H．∵斜坡AP的坡度为5：12，∴．设k米，则k米，由勾股定理，得米．∴，解得．∴．答：坡顶A到地面PQ的距离为5米．H(2)树BC的高度（结果精确到1米）.（参考数据：，，）（2）解：延长BC交PQ于点D．∵，，∴．∴四边形AHDC是矩形，，．∵，∴．设米，则，由（1）知：，∴，∴，∴．HD在中，，即，∴．答：树BC的高度约为9米．如图，一座山的一段斜坡BD的长度为400米，且这段斜坡的坡度（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角（即）为，在斜坡D处测得山顶A的仰角（即）为．求山顶A到地面的高度是多少米？解：作于H．设．∵，在中，，∴，在中，∵，∴，如图，一座山的一段斜坡BD的长度为400米，且这段斜坡的坡度（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角（即）为，在斜坡D处测得山顶A的仰角（即）为．求山顶A到地面的高度是多少米？又∵，∴，在中，，∴，∴答：山顶A到地面的高度是米．1.如图，小雅家(图中点O处)门前有一条东西走向的公路，测得有一水塔(图中点A处)在她家北偏东60°的500m处，那么水塔所在的位置到公路的距离AB是()A.250mB.250mC.500mD.250m2.如图所示，河堤横断面迎水坡AB的坡比是1:,堤高BC=5m，则坡面AB的长度是()A.5mB.10mC.10mD.15mAC3.如图，将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下，使木桩向上运动，已知楔子斜面的倾斜角为20°，若楔子沿水平方向前移8cm(如箭头所示),则木桩上升了()A.8sin20°B.C.8cos20°D.8tan20°820tanD820tan4.如图,(1)若h=2cm,a=5cm,则i=_____;(2)若i=1:,则∠A=_____.5.如图，水库的横断面是梯形ABCD,迎水坡AB的坡度i=1:1,坝高BE=20m，迎水坡AB=_____m,坡角α=______.2:530°2045°6.如图，在一笔直的海岸线上有A、B两个观测站，A在B的正西方向，AB=2km，从A测得船C在北偏东45°的方向，从B测得船C在北偏西30°的方向，则船C离海岸线的距离是______km.(结果保留根号)(3)7.如图，海中有一个小岛A，该岛四周15海里内有暗礁.今有货轮由西向东航行，开始在A岛南偏西55°的B处，往东行驶20海里后到达该岛的南偏西25°的C处.之后，货轮继续向东航行.你认为货轮继续向东航行途中会有触礁的危险吗?解:如图，过点A作AD⊥BC交BC延长线于点D.根据题意可知，∠BAD=55°,∠CAD=25°,BC=20海里.在Rt△ABD中，∵tan55°=，∴BD=ADtan55°在Rt△ACD中，∵tan25°=，∴CD=ADtan25°∵BD-CD=20∴AD(tan55°-tan25°)=20解得，AD≈20.8∵20.8>15∴东货轮继续向东航行，途中.不会有触礁的危险.BDADCDADBDADCDAD8.为了学生的安全，某校决定把一段如图所示的步梯路段进行改造.已知四边形ABCD为矩形，DE=10m，其坡度为i1=1:,将步梯DE改造为斜坡AF，其坡度为i2=1:4，求斜坡AF的长度(结果精确到0.01m，参考数据:≈1.732，≈4.123).解:∵DE=10m，其坡度为i1=1:∴CE=CD由勾股定理得,解得CD=5m∵四边形ABCD为矩形，∴AB=CD=5m∵斜坡AF的坡度为i2=1:4∴∴BF=4AB=20m在Rt△ABF中，故斜坡AF的长度约为20.62m.22210DECDCECDm14ABBF225172062.()AFABBFm22210DECDCECDm14ABBF225172062.()AFABBFm