2022年秋青岛版初中数学九年级上册--锐角三角比-课件



2.1锐角三角比11、探索锐角三角比的概念、探索锐角三角比的概念..22、能叙述锐角三角比的概念,记住三角、能叙述锐角三角比的概念,记住三角比的符号,掌握锐角三角比的表示方法比的符号,掌握锐角三角比的表示方法..33、会求直角三角形中指定锐角的三角比、会求直角三角形中指定锐角的三角比..•1.相似三角形的性质•2.勾股定理•3.Rt△ABC中,斜边是(),∠A的对边是(),∠A的邻边是().ABC回顾思考:根据现有知识,会解下列各题吗?(1)已知:在直角三角形中,AC=4,BC=3,求∠A.(2)已知:在直角三角形中,AC=4,∠A=25°,求:BC.显然,不能。怎么办呢?ACB┏生活中的梯子梯子是我们日常生活中常见的物体.情境导入上图为一社区幼儿园的滑梯,为了确保小朋友在玩耍过程中能更加安全你能否用你学过的知识利用钢管为小朋友们将这个滑梯变得更加牢固呢?ABCB1C1C2C3C4B2B3B4木板上的点到A点的距离/米距地面的高度/米B10.800.40B21.000.50B31.200.60B41.500.75利用上述数据,计算,,,,的值,你有什么发现?ABBC111ABCB222ABCB333ABCB444ABCB444ABCB333ABCB222ABCB111ABCBABBCABCB1C1新知探索在Rt△ABC中,点B1在斜边AB上,过点B1作B1C1⊥AC与C1。求证:(1)△ABC∽△AB1C1ABBCABCB1112)(证明:∵B1C1AC⊥∴∠ACB=AC∠1B1=90°∵∠A=A∠∴Rt△ABCRt∽△AB1C1ABBCABCB111ABABBCCB111ABCB1C1结论:结论:只要锐角只要锐角AA的度数一的度数一定,定,∠∠AA无论在哪一个直角无论在哪一个直角三角形中,它的对边与斜边三角形中,它的对边与斜边的比值都是不变的(定值)。的比值都是不变的(定值)。如图,我们知道:当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其他边之间的比值也确定吗?结论:在Rt△ABC中,如果锐角A确定时,那么∠A的对边与斜边的比,邻边与斜边的比也随之确定.ABC∠A的对边∠A的邻边┌斜边ABCB1C1C2C3C4B2B3B4木板上的点到A点的距离/米距地面的高度/米B10.800.40B21.000.50B31.200.60B41.500.75利用上述数据,计算,,,,的值,你有什么发现?ABBC111ABCB222ABCB333ABCB444ABCB444ABCB333ABCB222ABCB111ABCBABBCABC斜边∠A的邻边∠A的对边由锐角A确定的比叫做∠A的正弦,∠A的对边斜边sinA=∠A的对边斜边记作sinA,即由锐角A确定的比叫做∠A的余弦,∠A的邻边斜边cosA=∠A的邻边斜边记作cosA,即∠A的对边∠A的邻边由锐角A确定的比叫做∠A的正切,记作tanA,即tanA=∠A的对边∠A的邻边锐角A的正弦、余弦、正切统称锐角A的三角比.一个锐角A的三角比只与它的大小有关.在直角三角形中,锐角A的对边与斜边的比叫做∠A的正弦;sinA=∠A的对边斜边记作sinA,即锐角三角比正弦:正弦:ACB┏∠B的正弦怎么表示呢?结论:梯子的倾斜程度与sinA和cosA有关:sinA越大,梯子越陡;cosA越小,梯子越陡.如图,梯子的倾斜程度与sinA和cosA有关吗?AC2C1B2B11、正弦:在直角三角形中,锐角A的对边与斜边的比叫做∠A的正弦;sinA=∠A的对边斜边记作sinA,即一、锐角三角比ACB┏2、余弦:在直角三角形中,锐角A的邻边与斜边的比叫做∠A的余弦;cosA=∠A的邻边斜边记作cosA,即3、正切:在直角三角形中,锐角A的对边与邻边的比叫做∠A的正切。记作tanA,即tanA=∠A的对边∠A的邻边锐角A的正弦、余弦、正切统称锐角A的三角比.课堂小结通过这节课的学习,相信同学们一定学到了不少的新的知识了吧,课下一定要积极的落实,对新学的知识进行复习巩固,对新知识预习
提供2022年秋青岛版初中数学九年级上册--锐角三角比-课件会员下载,编号:1701028262,格式为 xlsx,文件大小为16页,请使用软件:wps,office Excel 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载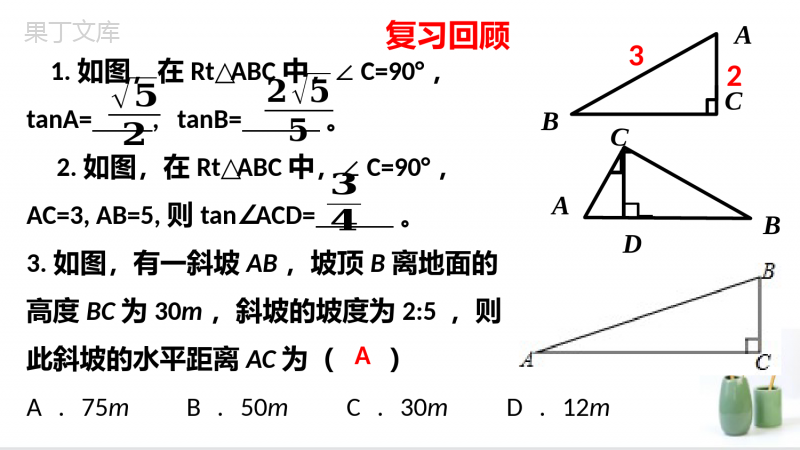 下载
下载 下载
下载 下载
下载