《函数的单调性与导数》人教版高中数学选修2-2PPT课件（第1.3.1课时）.pptx

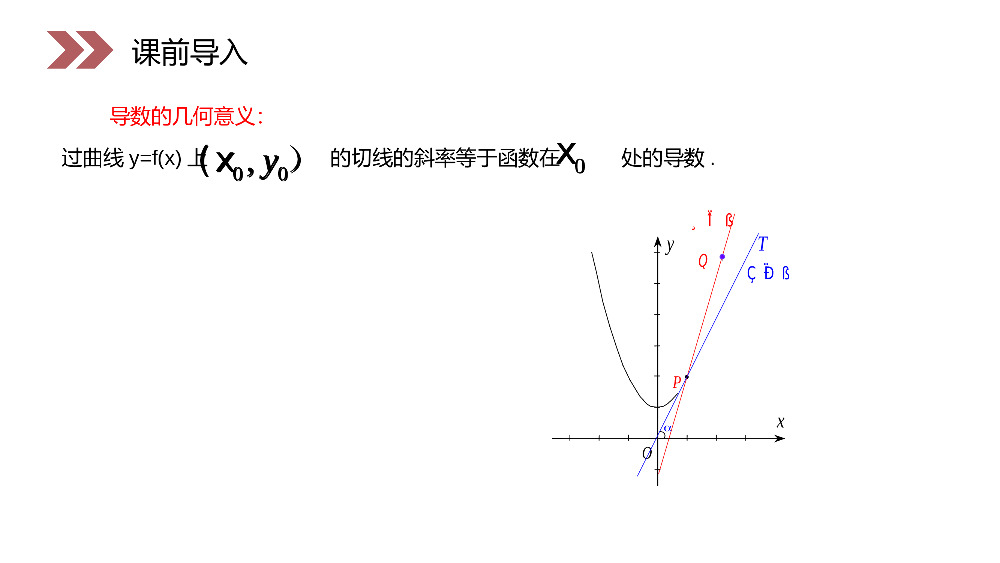
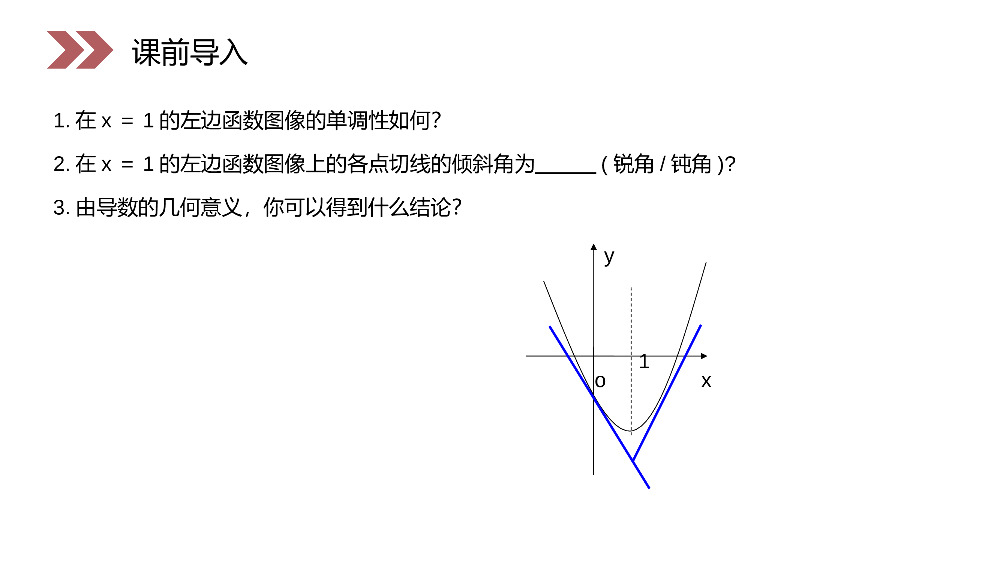
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.3.1函数的单调性与导数第1章导数及其应用人教版高中数学选修2-2'''1).;fxgxfxgx'''2).;fxgxfxgxfxgx导数运算法则课前导入'''23).0.fxfxgxfxgxgxgxgx'''1).;fxgxfxgx'''2).;fxgxfxgxfxgx'''23).0.fxfxgxfxgxgxgxgxPxyOTQ¸îÏßÇÐÏß导数的几何意义：过曲线y=f(x)上的切线的斜率等于函数在处的导数.00,y(x）0x课前导入00,y(x）0xox1y2.在x＝1的左边函数图像上的各点切线的倾斜角为(锐角/钝角)?3.由导数的几何意义，你可以得到什么结论？1.在x＝1的左边函数图像的单调性如何？课前导入函数y=f(x)在给定区间G上，当x1、x2G∈且x1＜x2时1）都有f(x1)＜f(x2)，则f(x)在G上是增函数；2）都有f(x1)＞f(x2)，则f(x)在G上是减函数.课前导入函数单调性判定yxoabyxoab若f(x)在G上是增函数或减函数，G称为单调区间G=(a,b)则f(x)在G上具有严格的单调性.课前导入单调函数的图象特征导数应用的知识网络结构图：课前导入课前导入htom()hftM新知探究观察()hftM上面函数图像中，它表示高台跳水运动员的高度h随时间变化的函数2h(t)=-4.9t+6.5t+10的图像.运动员从起跳到最高点，以及从最高点到入水这两段时间内，随着时间的变化，运动员离水面的高度发生什么变化？htom()hftM新知探究2h(t)=-4.9t+6.5t+10()hftM?性呢这种情况是否具有一般思考通过观察图像，我们可以发现：（1）运动员从起跳到最高点，离水面高度h随时间t的增加而增加，即h(t)是增函数.相应的，'vt=ht>0.（2）从最高点到入水，运动员离水面高度h随时间t的增加而减少，即h(t)是减函数.相应的，'vt=ht<0.新知探究?性呢这种情况是否具有一般思考'vt=ht>0.'vt=ht<0.yoxxyoxyoxy1yx2yx3yx函数在R上'()10fx（-∞，0）（0，+∞）'()20fxx'()20fxx函数在R上2'()30fxx（-∞，0）2'()0fxx（0，+∞）2'()0fxxyox新知探究观察下面函数的图像，探讨函数的单调性xy1yx2yx3yx'()10fx'()20fxx'()20fxx2'()30fxx2'()0fxx2'()0fxx在某个区间（a，b）内，①如果f’(x)>0，那么函数y=f(x)在这个区间内单调递增.②如果f’(x)<0，那么函数y=f(x)在这个区间内单调递减.新知探究函数单调性与导数的关系1.如果在某个区间内恒有f’(x)＝0，那么函数f(x)有什么特性？2.回顾一下函数单调性的定义，利用平均变化率的几何意义，研究单调性的定义与其导数正负的关系？新知探究已知导函数f’(x)下列信息：①当10;②当x>4,或x<1时，f’(x)<0;③当x=4,或x=1时，f’(x)=0.试画出函数f(x)图象的大致形状.新知探究例1O14xyy=f(x)解当10，可知f(x)在此区间内单调递增；当x>4或x<1时，f′(x)<0，可知f(x)在此区间内单调递减；当x=4或x=1时，f′(x)=0，这两点比较特殊，我们称它们为“临界点”.综上，函数f(x)图像的大致形状如右图所示.新知探究22()23121fxxxx判断函数的单调性，并求出其单调区间.2f'(x)=6x+6x-12因为32f(x)=2x+3x-12x+1所以当x>1x<-2或时，函数32f(x)=2x+3x-12x+1单调递增.当-21x<-2或时，32f(x)=2x+3x-12x+1-20，解得x>2或x<0∴当x(2,∈＋∞)时，f(x)是增函数；当x(∈－∞，0)时，f(x)也是增函数令6x2－12x<0，解得00.解因为所以3,fx=x+3xxR,1.3-51.因此函数在上单调递增如图所示xyox3xxf3153.1图判断下列函数的单调性，并求出单调区间：新知探究例432321fx=x+3x;2fx=x-2x-3;3fx=sinx-x,x0,π;4fx=2x+3x-24x+1.3'221fx=x+3x,fx=3x+3=3x+1>0.解因为所以3,fx=x+3xxR,1.3-51.因此函数在上单调递增如图所示xyox3xxf3153.1图2'2fx=x-2x-3,fx=2x-2=2x-1.因为所以'2fx>0,x>1,fx=x-2x-3;当即时函数单调递增'2fx<0,x<1,fx=x-2x-3.当即时函数单调递减2fx=x-2x-31.3-52.函数的图象如图所示xyo2fx=x-2x-31.3-521新知探究2'2fx=x-2x-3,fx=2x-2=2x-1.因为所以'2fx>0,x>1,fx=x-2x-3;当即时函数单调递增'2fx<0,x<1,fx=x-2x-3.当即时函数单调递减2fx=x-2x-31.3-52.函数的图象如图所示xyo2fx=x-2x-31.3-521xyofx=sinx-xn1.3-53π.xf,π,0x,xxsinxf3'所以因为.353.1.π,0x,xxsinxf,所示如图内函数因此cosx-1递减新知探究xyofx=sinx-xn1.3-53π.xf,π,0x,xxsinxf3'所以因为.353.1.π,0x,xxsinxf,所示如图内函数因此.453.11x24x3x2xf23所示的图象如图因为所以324fx2x3x24x1,;xf,,0xf'函数时即当.xf,,0xf'函数时即当15Oxy1x24x3x2xf23453.1图2f(x)6x6x24′新知探究.453.11x24x3x2xf23所示的图象如图因为所以324fx2x3x24x1,;xf,,0xf'函数时即当.xf,,0xf'函数时即当15Oxy1x24x3x2xf23453.1图2f(x)6x6x24′（1）确定函数y=f(x)的定义域；（2）求导数f’(x)；（3）解不等式f’(x)>0，解集在定义域内的部分为增区间；（4）解不等式f’(x)<0，解集在定义域内的部分为减区间．新知探究你能小结求解函数单调区间的步骤吗？如图1.3-6，水以恒速（即单位时间内注入水的体积相同）注入下面四种底面积相同的容器中，试分别找出与各容器对应的高度h与时间t的函数关系图像.新知探究例463.1图1234AothBothCothDoth63.1图1234AothBothCothDoth解1→B,2→A,3→D,4→C.例4表明，通过函数图像，不仅可以看出函数的增与减，还可以看出其增减的快慢.结合图像，你能从导数的角度解释增减快慢的情况吗？新知探究解1→B,2→A,3→D,4→C.oxyaa73.1图一般地，如果一个函数在某一范围内导数的绝对值较大，函数的图像就比较“陡峭”，反之，函数的图像就“平缓”一些.如图所示.新知探究结论oxyaa73.1图函数3yaxx在R上是减函数，则（）.1Ba.0Ca.0Da1.3AaD课堂练习3yaxx.1Ba.0Ca.0Da1.3Aa设函数f(x)在定义域内可导，y=f(x)的图象如右图所示，则导函数y=f’(x)的图象可能是（）(A)(B)(C)(D)D课堂练习已知函数f(x)=kx3-3(k+1)x2-k2+1(k>0)，若f(x)的单调减区间为(0,4)，则k=____.1课堂练习已知函数,则f(x)的单调减区间为________.2()24fxxx,12()24fxxx,1确定函数f(x)=x2-2x+4在哪个区间内是增函数,哪个区间内是减函数.解:f(x)=2x-2.由2x-2>0,解得x>1，因此,当时,f(x)是增函数;(1,)x令2x-2<0,解得x<1，因此,当时,f(x)是减函数.(,1)x课堂练习f(x)=2x-2.(1,)x(,1)x讨论f(x)=x3-6x2+9x-3的单调性.解:f'(x)=3x2-12x+9令3x2-12x+9>0,解得x>3或x<1,因此,当或时，f(x)是增函数.(3,)x(,1)x令3x2-12x+9<0,解得10,那么函数y=fx在这个区间内单调递增;如果fx<0,那么函数y=fx在这个区间内单调递减.一般地,函数的单调性与导数的关系：课堂小结利用函数的导数来研究函数的单调性.其基本的步骤为:①求函数的定义域;②求函数的导数;)(xf③解不等式>0得f(x)的单调递增区间;解不等式<0得f(x)的单调递减区间.)()(xfxf''在某个区间a,b内,如果fx>0,那么函数y=fx在这个区间内单调递增;如果fx<0,那么函数y=fx在这个区间内单调递减.)(xf)()(xfxf感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2