2023年中考数学复习最新真题源专题讲义专题讲义(七)-锐角三角函数

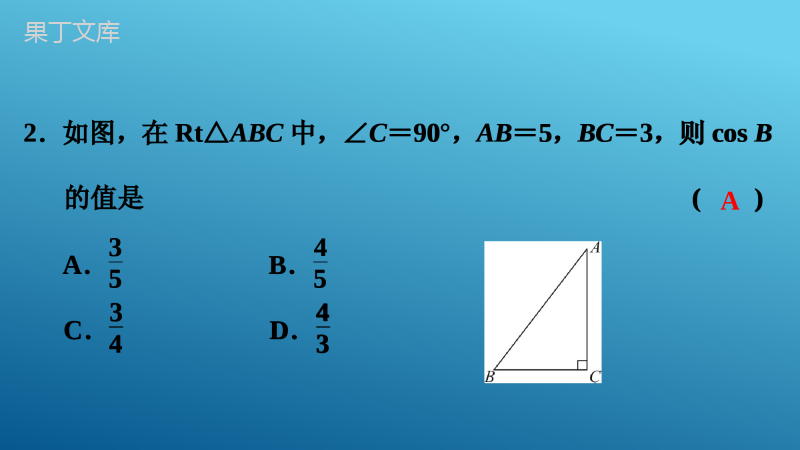
专题讲义(七)锐角三角函数专题讲义(七)锐角三角函数一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．以下列长度的三条线段为边，不能组成直角三角形的是()A．1，2，3B．3，4，5C．50，120，130D．1，2，3D一、选择题：本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．以下列长度的三条线段为边，不能组成直角三角形的是()A．1，2，3B．3，4，5C．50，120，130D．1，2，32．如图，在Rt△ABC中，∠C＝90°，AB＝5，BC＝3，则cosB的值是()A．35B．45C．34D．43A2．如图，在Rt△ABC中，∠C＝90°，AB＝5，BC＝3，则cosB的值是()A．35B．45C．34D．433．如图，在平面直角坐标系中，点A的坐标为(4，3)，那么cosα的值是()A．34B．43C．35D．45D3．如图，在平面直角坐标系中，点A的坐标为(4，3)，那么cosα的值是()A．34B．43C．35D．454．在Rt△ABC中，∠C＝90°，AC＝1，BC＝3，则∠A的正切值为()A．3B．13C．1010D．31010A4．在Rt△ABC中，∠C＝90°，AC＝1，BC＝3，则∠A的正切值为()A．3B．13C．1010D．310105．在Rt△ABC中，cosA＝12，那么sinA的值是()A．22B．32C．33D．12B5．在Rt△ABC中，cosA＝12，那么sinA的值是()A．22B．32C．33D．126．在正方形网格中，△ABC的位置如图所示，则cosB的值为()A．22B．32C．33D．1A6．在正方形网格中，△ABC的位置如图所示，则cosB的值为()A．22B．32C．33D．17．(2022·福建)如图所示的衣架可以近似看成一个等腰三角形ABC，其中AB＝AC，∠ABC＝27°，BC＝44cm，则高AD约为()(参考数据：sin27°≈0.45，cos27°≈0.89，tan27°≈0.51)A．9.90cmB．11.22cmC．19.58cmD．22.44cmB7．(2022·福建)如图所示的衣架可以近似看成一个等腰三角形ABC，其中AB＝AC，∠ABC＝27°，BC＝44cm，则高AD约为()(参考数据：sin27°≈0.45，cos27°≈0.89，tan27°≈0.51)A．9.90cmB．11.22cmC．19.58cmD．22.44cm8．在△ABC中，∠C＝90°，AB＝6，cosA＝13，则AC等于()A．18B．2C．12D．118B8．在△ABC中，∠C＝90°，AB＝6，cosA＝13，则AC等于()A．18B．2C．12D．1189．如图，在四边形ABCD中，∠B＝90°，AB＝2，CD＝8，AC⊥CD，若sin∠ACB＝13，则cos∠ADC的值为()A．34B．45C．35D．22B9．如图，在四边形ABCD中，∠B＝90°，AB＝2，CD＝8，AC⊥CD，若sin∠ACB＝13，则cos∠ADC的值为()A．34B．45C．35D．2210．如图，要测量小河两岸相对的两点P，A的距离，可以在小河边取PA的垂线PB上的一点C，测得PC＝100米，∠PCA＝35°，则小河宽PA等于()A．100sin35°米B．100sin55°米C．100tan35°米D．100tan55°米C10．如图，要测量小河两岸相对的两点P，A的距离，可以在小河边取PA的垂线PB上的一点C，测得PC＝100米，∠PCA＝35°，则小河宽PA等于()A．100sin35°米B．100sin55°米C．100tan35°米D．100tan55°米二、填空题：本大题共5小题，每小题3分，共15分．11．计算：tan45°－2cos60°＝___.12．在直角三角形ABC中，若2AB＝AC，则cosC＝__________.13．如图，AB和⊙O切于点B，AB＝4，OB＝3，则tanA＝____.032或25534二、填空题：本大题共5小题，每小题3分，共15分．11．计算：tan45°－2cos60°＝___.12．在直角三角形ABC中，若2AB＝AC，则cosC＝__________.13．如图，AB和⊙O切于点B，AB＝4，OB＝3，则tanA＝____.32或2553414．如图，在△ABC中，∠C＝90°，sinA＝45，AB＝10，则△ABC的周长为____.2414．如图，在△ABC中，∠C＝90°，sinA＝45，AB＝10，则△ABC的周长为____.15．如图，在△ABC中，∠C＝60°，AC＝2，BC＝3，则tanB的值为_____.3215．如图，在△ABC中，∠C＝60°，AC＝2，BC＝3，则tanB的值为_____.32三、解答题(一)：本大题共3小题，每小题8分，共24分．16.计算：(12)－1＋(π－3)0－2cos30°＋3－12.解：原式＝2＋1－2×32＋23－3＝3.＝3－3＋23－3三、解答题(一)：本大题共3小题，每小题8分，共24分．16.计算：(12)－1＋(π－3)0－2cos30°＋3－12.解：原式＝2＋1－2×32＋23－3＝3.＝3－3＋23－317．在△ABC中，∠A，∠B满足sinA－32＋(1－3tanB)2＝0，试判断△ABC的形状，并说明理由．解：直角三角形．理由如下：由题意，得sinA－32＝0，1－3tanB＝0，解得sinA＝32，tanB＝33，∴∠A＝60°，∠B＝30°，则∠C＝180°－60°－30°＝90°.故△ABC为直角三角形．17．在△ABC中，∠A，∠B满足sinA－32＋(1－3tanB)2＝0，试判断△ABC的形状，并说明理由．解：直角三角形．理由如下：由题意，得sinA－32＝0，1－3tanB＝0，解得sinA＝32，tanB＝33，∴∠A＝60°，∠B＝30°，则∠C＝180°－60°－30°＝90°.故△ABC为直角三角形．18．如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，求大厅两层之间的距离BC的长．(结果精确到0.1米；参考数据：sin31°＝0.515，cos31°＝0.857，tan31°＝0.60)解：在Rt△ABC中，∵∠ACB＝90°，∴BC＝AB·sin∠BAC＝12×0.515≈6.2(米)．即大厅两层之间的距离BC的长约为6.2米．18．如图，某商店营业大厅自动扶梯AB的倾斜角为31°，AB的长为12米，求大厅两层之间的距离BC的长．(结果精确到0.1米；参考数据：sin31°＝0.515，cos31°＝0.857，tan31°＝0.60)解：在Rt△ABC中，∵∠ACB＝90°，∴BC＝AB·sin∠BAC＝12×0.515≈6.2(米)．即大厅两层之间的距离BC的长约为6.2米．四、解答题(二)：本大题共3小题，每小题9分，共27分．19．(2022·河池)如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD＝36m，求居民楼AB的高度．(结果保留整数．参考数据：sin33°≈0.55，cos33°≈0.84，tan33°≈0.65)四、解答题(二)：本大题共3小题，每小题9分，共27分．19．(2022·河池)如图，小敏在数学实践活动中，利用所学知识对他所在小区居民楼AB的高度进行测量，从小敏家阳台C测得点A的仰角为33°，测得点B的俯角为45°，已知观测点到地面的高度CD＝36m，求居民楼AB的高度．(结果保留整数．参考数据：sin33°≈0.55，cos33°≈0.84，tan33°≈0.65)解：如图，过点C作CE丄AB，垂足为E，由题意得，CD＝36m，∠BCE＝45°，∠ACE＝33°，在Rt△BCE中，∠BCE＝45°，∴BE＝CE＝CD＝36m，在Rt△ACE中，∠ACE＝33°，CE＝36m，∴AE＝CE·tan33°≈23.4m，∴AB＝AE＋BE＝36＋23.4＝59.4≈59(m)．答：居民楼AB的高度约为59m.解：如图，过点C作CE丄AB，垂足为E，由题意得，CD＝36m，∠BCE＝45°，∠ACE＝33°，在Rt△BCE中，∠BCE＝45°，∴BE＝CE＝CD＝36m，在Rt△ACE中，∠ACE＝33°，CE＝36m，∴AE＝CE·tan33°≈23.4m，∴AB＝AE＋BE＝36＋23.4＝59.4≈59(m)．答：居民楼AB的高度约为59m.20．如图，已知矩形ABCD.(1)尺规作图：在BC上方求作△FBC，使得FB＝FC，且点F与点A关于过点B的直线对称；(保留作图痕迹，不写作法)(2)在(1)的条件下，若AB＝3，BC＝5，求sin∠ABF的值．20．如图，已知矩形ABCD.(1)尺规作图：在BC上方求作△FBC，使得FB＝FC，且点F与点A关于过点B的直线对称；(保留作图痕迹，不写作法)(2)在(1)的条件下，若AB＝3，BC＝5，求sin∠ABF的值．解：(1)如图，△FBC即为所求作．解：(1)如图，△FBC即为所求作．解：(2)设MN交BC于点T.∵MN垂直平分线段BC，AB⊥BC，∴MN∥AB，∴∠ABF＝∠BFT，又∵点F与点A关于过点B的直线对称，∴BF＝AB＝3.∴sin∠ABF＝sin∠BFT＝BTBF＝523＝56.解：(2)设MN交BC于点T.∵MN垂直平分线段BC，AB⊥BC，∴MN∥AB，∴∠ABF＝∠BFT，又∵点F与点A关于过点B的直线对称，∴BF＝AB＝3.∴sin∠ABF＝sin∠BFT＝BTBF＝523＝56.21．(2022·绥化)如图所示，为了测量百货大楼CD顶部广告牌ED的高度，在距离百货大楼30m的A处用仪器测得∠DAC＝30°；向百货大楼的方向走10m，到达B处时，测得∠EBC＝48°，仪器高度忽略不计，求广告牌ED的高度．(结果保留小数点后一位)(参考数据：3≈1.732，sin48°≈0.743，cos48°≈0.669，tan48°≈1.111)21．(2022·绥化)如图所示，为了测量百货大楼CD顶部广告牌ED的高度，在距离百货大楼30m的A处用仪器测得∠DAC＝30°；向百货大楼的方向走10m，到达B处时，测得∠EBC＝48°，仪器高度忽略不计，求广告牌ED的高度．(结果保留小数点后一位)(参考数据：3≈1.732，sin48°≈0.743，cos48°≈0.669，tan48°≈1.111)解：在Rt△ADC中，∠DAC＝30°，AC＝30米，∴CD＝AC·tan30°＝30×33＝103(米)，∵AB＝10米，∴BC＝AC－AB＝20米，在Rt△BCE中，∠EBC＝48°，∴EC＝BC·tan48°≈20×1.111＝22.22(米)，∴DE＝EC－DC＝22.22－103≈4.9(米)，∴广告牌ED的高度约为4.9米．解：在Rt△ADC中，∠DAC＝30°，AC＝30米，∴CD＝AC·tan30°＝30×33＝103(米)，∵AB＝10米，∴BC＝AC－AB＝20米，在Rt△BCE中，∠EBC＝48°，∴EC＝BC·tan48°≈20×1.111＝22.22(米)，∴DE＝EC－DC＝22.22－103≈4.9(米)，∴广告牌ED的高度约为4.9米．五、解答题(三)：本大题共2小题，每小题12分，共24分．22．(2022·广元)如图，计划在山顶A的正下方沿直线CD方向开通穿山隧道EF.在点E处测得山顶A的仰角为45°，在距E点80m的C处测得山顶A的仰角为30°，从与F点相距10m的D处测得山顶A的仰角为45°，点C，E，F，D在同一直线上，求隧道EF的长度．五、解答题(三)：本大题共2小题，每小题12分，共24分．22．(2022·广元)如图，计划在山顶A的正下方沿直线CD方向开通穿山隧道EF.在点E处测得山顶A的仰角为45°，在距E点80m的C处测得山顶A的仰角为30°，从与F点相距10m的D处测得山顶A的仰角为45°，点C，E，F，D在同一直线上，求隧道EF的长度．解：如图，过点A作AH丄DE，垂足为H，设EH＝x米，在Rt△AEH中，∠AEH＝45°，∴AH＝EH·tan45°＝x米，∵CE＝80米，∴CH＝CE＋EH＝(80＋x)米，在Rt△ACH中，∠ACH＝30°，∵tan30°＝AHCH＝x80＋x＝33，∴x＝403＋40，经检验：x＝403＋40是原方程的根，解：如图，过点A作AH丄DE，垂足为H，设EH＝x米，在Rt△AEH中，∠AEH＝45°，∴AH＝EH·tan45°＝x米，∵CE＝80米，∴CH＝CE＋EH＝(80＋x)米，在Rt△ACH中，∠ACH＝30°，∵tan30°＝AHCH＝x80＋x＝33，∴x＝403＋40，经检验：x＝403＋40是原方程的根，∴AH＝EH＝(403＋40)米，在Rt△AHD中，∠ADH＝45°，∴DH＝AHtan45°＝(403＋40)米，∴EF＝EH＋DH－DF＝(803＋70)米，∴隧道EF的长度为(803＋70)米．∴AH＝EH＝(403＋40)米，在Rt△AHD中，∠ADH＝45°，∴DH＝AHtan45°＝(403＋40)米，∴EF＝EH＋DH－DF＝(803＋70)米，∴隧道EF的长度为(803＋70)米．23．(2021·苏州)如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED.(1)求证：BD＝ED；(2)若AB＝4,BC＝6,∠ABC＝60°.求tan∠DCB的值．23．(2021·苏州)如图，四边形ABCD内接于⊙O，∠1＝∠2，延长BC到点E，使得CE＝AB，连接ED.(1)求证：BD＝ED；(2)若AB＝4,BC＝6,∠ABC＝60°.求tan∠DCB的值．(1)证明：∵四边形ABCD内接于⊙O，∴∠A＝∠DCE，∵∠1＝∠2，∴AD︵＝DC︵，∴AD＝DC，在△ABD和△CED中，AB＝CE，∠A＝∠DCE，AD＝CD，∴△ABD≌△CED(SAS)，∴BD＝ED；(1)证明：∵四边形ABCD内接于⊙O，∴∠A＝∠DCE，∵∠1＝∠2，∴AD︵＝DC︵，∴AD＝DC，在△ABD和△CED中，AB＝CE，∠A＝∠DCE，AD＝CD，∴△ABD≌△CED(SAS)，∴BD＝ED；(2)解：如图，过点D作DM⊥BE于点M，∵AB＝4，BC＝6，CE＝AB，∴BE＝BC＋CE＝10，∵BD＝ED，DM⊥BE，∴BM＝ME＝12BE＝5，∴CM＝BC－BM＝1，∵∠ABC＝60°，∠1＝∠2，∴∠2＝30°，∴DM＝BM·tan∠2＝5×33＝533，∴tan∠DCB＝DMCM＝533.(2)解：如图，过点D作DM⊥BE于点M，∵AB＝4，BC＝6，CE＝AB，∴BE＝BC＋CE＝10，∵BD＝ED，DM⊥BE，∴BM＝ME＝12BE＝5，∴CM＝BC－BM＝1，∵∠ABC＝60°，∠1＝∠2，∴∠2＝30°，∴DM＝BM·tan∠2＝5×33＝533，∴tan∠DCB＝DMCM＝533.