《概率的基本性质》人教版高中数学必修三PPT课件（第3.1.3课时）.pptx

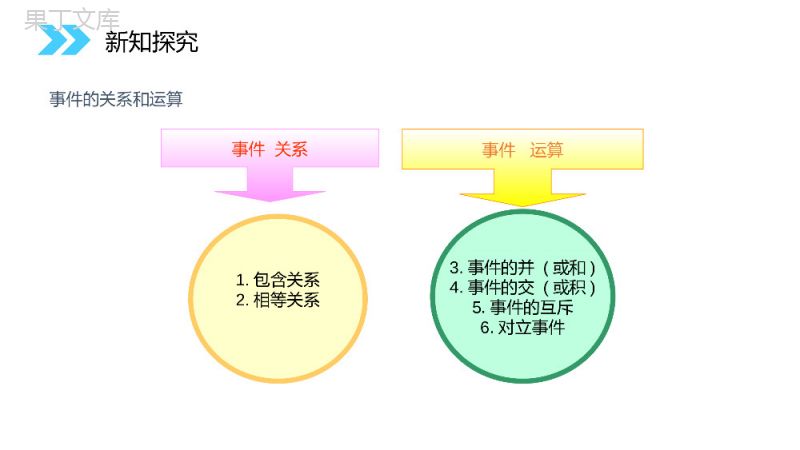
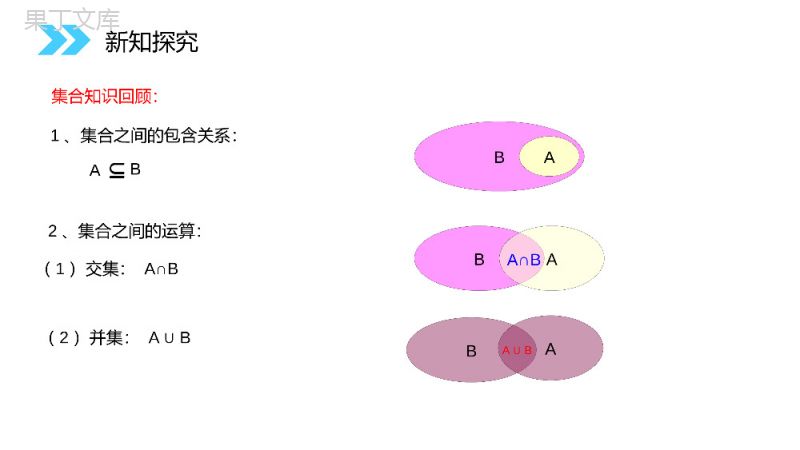
讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT3.1.3概率的基本性质第3章概率人教版高中数学必修31.了解事件间的相互关系；2.理解互斥事件、对立事件的概念；3.会用概率加法公式求某些事件的概率。重点与难点重点：事件的关系、运算与概率的性质；难点：事件关系的判定。学习目标事件的关系和运算1.包含关系2.相等关系3.事件的并(或和)4.事件的交(或积)5.事件的互斥6.对立事件事件运算事件关系新知探究集合知识回顾：1、集合之间的包含关系：BA2、集合之间的运算：BA（1）交集：A∩B（2）并集：AB∪ABBAA∩B新知探究AB∪我们知道，一个事件可能包含试验的多个结果。比如在掷骰子这个试验中：“出现的点数小于或等于3”这个事件中包含了哪些结果呢？①“出现的点数为1”“②出现的点数为2”③“出现的点数为3”这三个结果这样我们把每一个结果可看作元素，而每一个事件可看作一个集合。因此，事件之间的关系及运算几乎等价于集合之间的关系与运算。新知探究在掷骰子的试验中，我们可以定义许多事件，如：（课本P119）问题引导下的再学习:你能写出这个试验中出现的其它一些事件吗?如：M={出现1点或2点}；N1={出现的点数小于7}；N2={出现的点数大于4}；类比集合与集合的关系、运算，探讨它们之间的关系与运算吗？新知探究BA1.包含关系若事件A发生则必有事件B发生，则称事件B包含事件A（或称事件A包含于事件B）,记为AB（或BA)。不可能事件记作，任何事件都包含不可能事件。新知探究例：某一学生数学测验成绩记A=｛95～100分｝B=｛优｝，说出A、B之间的关系。解：显然事件A发生必有事件B发生。记为AB（或BA）。例：事件C1={出现1点}发生，则事件H={出现的点数为奇数}也一定会发生，所以1CH新知探究1CHAB2.等价关系若事件A发生必有事件B发生；反之事件B发生必有事件A发生即，若AB，且BA，那么称事件A与事件B相等，记为A=B例.事件C1={出现1点}发生，则事件D1={出现的点数不大于1}就一定会发生，反过来也一样，所以C1=D1。新知探究例：从一批产品中抽取30件进行检查,记A=｛30件产品中至少有1件次品｝，B=｛30件产品中有次品｝。说出A与B之间的关系。显然事件A与事件B等价记为：A=B新知探究3.并事件（或称和事件）若某事件发生当且仅当事件A发生或事件B发生（即事件A，B中至少有一个发生），则称此事件为A与B的并事件（或和事件）记为AB（或A+B）。AB新知探究显然,事件C是事件A,B的并记为C=AB例:抽查一批零件,记事件A=“都是合格品”，B=“恰有一件不合格品”,C=“至多有一件不合格品”.说出事件A、B、C之间的关系。新知探究4.交事件（或积事件）若某事件发生当且仅当事件A发生且事件B发生（即“A与B都发生”），则称此事件为A与B的交事件（或积事件），记为AB或ABABC新知探究例：D2=｛出现点数大于3｝，D3=｛出现点数小于5｝，求D2∩D3.解：D2=｛出现点数为4,5,6｝，D3=｛出现点数为1,2,3,4｝D2∩D3=｛出现4点｝。新知探究例：某项工作对视力的要求是两眼视力都在1.01.0以上。记事件A=“左眼视力在1.0以上”事件B=“右眼视力在1.0以上”事件C=“视力合格”说出事件A、B、C的关系。显然，C=AB新知探究例、某检查员从一批产品中抽取8件进行检查，观察其中的次品数记：A=“次品数少于5件”;B=“次品数恰有2件”C=“次品数多于3件”;D=“次品数至少有1件”试写出下列事件的基本事件组成：AB∪，A∩C,B∩C;AB=A(∪A,B中至少有一个发生）A∩C=“有4件次品”B∩C=新知探究5.事件的互斥若A∩B为不可能事件（A∩B=），那么称事件A与事件B互斥，其含义是：事件A与B在任何一次试验中不会同时发生。AB即，A与B互斥AB=新知探究例：抽查一批产品，事件A=“没有不合格品”，事件B=“有一件不合格品”，问这两个事件能否在一次抽取中同时发生。显然，事件A与事件B是互斥的，也就是不可能同时发生的。即AB=新知探究例1.因为事件C1={出现1点}与事件C2={出现2点}不可能同时发生，故这两个事件互斥；D3={出现的点数小于5}与F={出现的点数大于6}不可能同时发生，故D3与F是互斥事件；G={出现的点数为偶数}与H={出现的点数为奇数}不可能同时发生，故事件G与事件H是互斥事件。新知探究6.对立事件若A∩B为不可能事件，AB∪必然事件，那么称事件A与事件B互为对立事件。其含义是：事件A与事件B在任何一次试验中有且仅有一个发生。AAB（）(,)ABAB新知探究A(,)ABAB例：从某班级中随机抽查一名学生，测量他的身高，记事件A=“身高在1.70m以上”，B=“身高不多于1.7m”说出事件A与B的关系。显然,事件A与B互为对立事件新知探究互斥事件是指事件A与事件B在一次试验中不会同时发生，其具体包括三种不同的情形：（1）事件A发生且事件B不发生；（2）事件B发生且事件A不发生；（3）事件A与事件B同时不发生；对立事件是指事件A与事件B有且仅有一个发生，其包括两种情形；（1）事件A发生B不发生；（2）事件B发生事件A不发生；对立事件是互斥事件的特殊情形。互斥事件与对立事件的区别与联系：新知探究对立事件一定是互斥事件互斥事件不一定是对立事件如：事件C1与C2是互斥事件，但不是对立事件例：G={出现的点数为偶数}与H={出现的点数为奇数}G∩H是不可能事件，GH∪是必然事件，故事件G与事件H是对立事件。区别：互斥事件：不同时发生，但并非至少有一个发生；对立事件：两个事件不同时发生，必有一个发生。新知探究2.从一堆产品（其中正品和次品都多于2件）中任取2件，观察正品件数和次品件数，判断下列每对事件是不是互斥事件，若是，再判断它们是不是对立事件：（1）恰好有1件次品和恰好有2件次品；（2）至少有1件次品和全是次品；（3）至少有1件正品和至少有1件次品；（4）至少有1件次品和全是正品。①正正②一正一次③次次②与③：互斥不对立②、③与③：不互斥不对立①、②与②、③：不互斥不对立②、③与①：互斥且对立新知探究至多有一个至少有两个至少有一个一个也没有总结：新知探究事件的关系和运算事件运算事件关系1.包含关系2.等价关系3.事件的并(或和)4.事件的交(或积)5.事件的互斥(或互不相容)6.对立事件(逆事件)新知探究二、概率的几个基本性质（1）、对于任何事件的概率的范围是：0≤P（A）≤1其中必然事件的概率是P（A）=1不可能事件的概率是P（A）=0思考：概率为1的事件是否为必然事件？概率为0的事件是否为不可能事件？新知探究（2）当事件A与事件B互斥时，AB∪的频率fn(AB)=∪fn(A)+fn(B)由此得到概率的加法公式：如果事件A与事件B互斥，则P（AB∪）=P（A）+P（B）注：事件A与B不互斥时，有P（AB∪）=P（A）+P（B）－P（AB)事件A与B互斥时，P（AB）=0，是特殊情况。新知探究例、抛掷骰子，事件A=“出现点数是奇数”，事件B=“出现点数不超过3”，求P（AB∪）解法一：因为P（A）=3/6=1/2，P（B）=3/6=1/2所以P（AB∪）=P（A）+P（B）=1解法二：AB∪这一事件包括4种结果，即出现1，2，3和5所以P（AB∪）=4/6=2/3请判断那种正确！新知探究概率的加法公式推广：若事件A1，A2，……，An彼此互斥，则:（3）特别地，若事件A与事件B互为对立事件，则AB∪为必然事件，P(AB)=1.∪再由加法公式得P(A)=1－P(B)，即1212()()()()nnpAAApApApA当事件A与事件B是对立事件时，有P（A）=1－P（B）新知探究1212()()()()nnpAAApApApA（1）取到红色牌（事件C）的概率是多少？（2）取到黑色牌（事件D）的概率是多少？例如果从不包括大小王的52张扑克牌中随机抽取一张，那么取到红心（事件A）的概率是，取到方片（事件B）的概率是。问:4141解：（1）因为C=AB∪，且A与B不会同时发生，所以A与B是互斥事件。根据概率的加法公式，得：P（C）=P（A）+P（B）=1/2（2）C与D也是互斥事件，又由于CD∪为必然事件，所以C与D互为对立事件，所以P（D）=1－P（C）=1/2新知探究4141临时小结：在求某些事件（如“至多、至少”）的概率时，通常有两种方法：1、将所求事件的概率化为彼此互斥的事件的和，用概率的加法公式求;2、先去求对立事件的概率，进而再求所求事件的概率．新知探究1、一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（）A.至多有一次中靶B.两次都不中靶B.C.只有一次中靶D.两次都不中靶2、下列各组事件中，不是互斥事件的是（）A.一个射手进行一次射击，命中环数大于8与命中环数小于6B.B.统计一个班级数学期中考试成绩，平均分数不低于90分与平均分数不高于90分C.C.播种菜籽100粒，发芽90粒与发芽80粒D.D.检查某种产品，合格率高于70％与合格率为70％BD课堂练习3.如果某士兵射击一次，未中靶的概率为0.05，求中靶概率。解：设该士兵射击一次，“中靶”为事件A,“未中靶”为事件B,则A与B互为对立事件，故P(A)=1-P(B)=1-0.05=0.95。课堂练习4.若A，B为互斥事件，则()(A)P(A)+P(B)<1(B)P(A)+P(B)>1(C)P(A)+P(B)=1(D)P(A)+P(B)≤1D5、某人射击1次，命中率如下表所示：命中环数10环9环8环7环6环及其以下（包括脱靶）概率0.120.180.280.320.1求射击1次，至少命中7环的概率为_____.0.9课堂练习6.甲，乙两人下棋，若和棋的概率是0.5，乙获胜的概率是0.3求：（1）甲获胜的概率；（2）甲不输的概率。解：(1)“甲获胜”是“和棋或乙获胜”的对立事件，因为“和棋”与“乙获胜”是互斥事件，所以甲获胜的概率为：1－（0.5+0.3）=0.2(2)设事件A={甲不输}，B={和棋}，C={甲获胜}则A=BC,∪因为B,C是互斥事件，所以P(A)=P(B)+P(C)=0.5+0.2=0.7课堂练习7.已知，在一商场付款处排队等候付款的人数及其概率如下：排队人数012345人以上概率0.10.160.30.30.10.04求至多2个人排队的概率。解：设事件Ak={恰好有k人排队}，事件A={至多2个人排队},因为A=A0A1A2,∪∪且A0，A1，A2这三个事件是互斥事件，所以P(A)=P(A0)+P(A1)+P(A2)=0.1+0.16+0.3=0.56。课堂练习8，有10名学生，其中4名男生，6名女生，从中任选2名，求恰好是2名男生或2名女生的概率.解：记“从中任选2名，恰好是2名男生”为事件A，“从中任选2名，恰好是2名女生”为事件B，则事件A与事件B为互斥事件，且“从中任选2名，恰好是2名男生或2名女生”为事件A+B.257()()().151515PABPAPB，，155)(152)(BPAP课堂练习257()()().151515PABPAPB，，155)(152)(BPAP9，袋中有12个小球，分别为红球、黑球、黄球、绿球，从中任取一球，得到红球的概率为，得到黑球或黄球的概率是，得到黄球或绿球的概率也是，试求得到黑球、得到黄球、得到绿球的概率各是多少？13512512解：从袋中任取一球，记事件“摸到红球”、“摸到黑球”、“摸到黄球”、“摸到绿球”为A、B、C、D，则有P(BC)=P(B)+P(C)=∪，解得，P(CD)=P(C)+P(D)=∪P(BCD)=1-P(A)=∪∪1251253241)D(P,61)C(P,41)B(P课堂练习135125121251253241)D(P,61)C(P,41)B(P8、某地区的年降水量在下列范围内的概率如下所示：年降水量（单位:mm)[100,150)[150,200)[200,250)[250,300)概率0.120.250.160.141.求年降水量在［100,200）（㎜）范围内的概率；2.求年降水量在［150,300）（mm)范围内的概率。解:(1)记这个地区的年降水量在[100,150)，[150,200)，[200,250)，[250,300)(mm)范围内分别为事件为A、B、C、D。这4个事件是彼此互斥的。根据互斥事件的概率加法公式，有(1)年降水量在［100,200）(mm)范围内的概率是P（A＋B）=P(A)+P(B)=0.12+0.25=0.37(2)年降水量在［150,300）(mm)内的概率是P(B+C+D)=P(B)+P(C)+P(D)=0.25+0.16+0.14=0.55.课堂练习1.事件的关系：包含关系、等价关系；2.事件的运算：事件的交、并以及对立事件和互斥事件；3.概率的基本性质及两个互斥事件加法公式的简单运用课堂小结感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明讲解人：办公资源时间：2020.6.1MENTALHEALTHCOUNSELINGPPT感谢你的聆听第3章概率人教版高中数学必修3