2022年秋青岛版初中数学九年级上册--解直角三角形的应用-2-课件

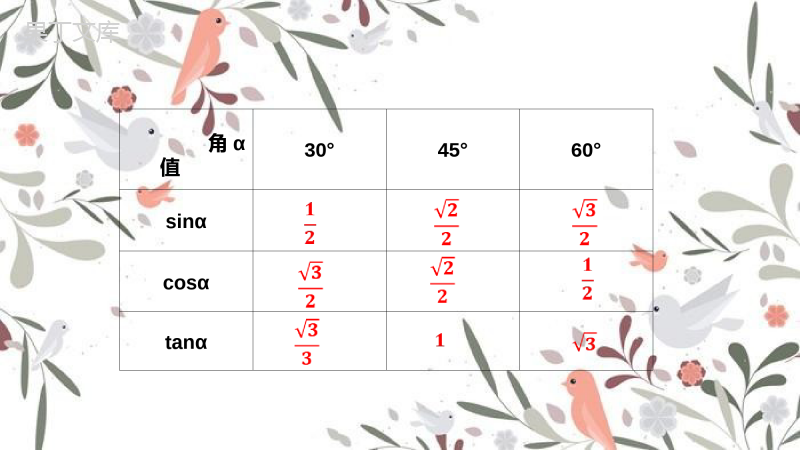
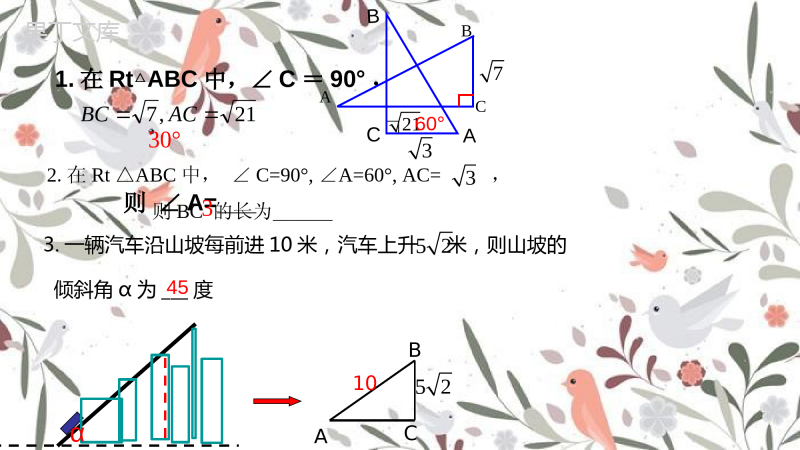
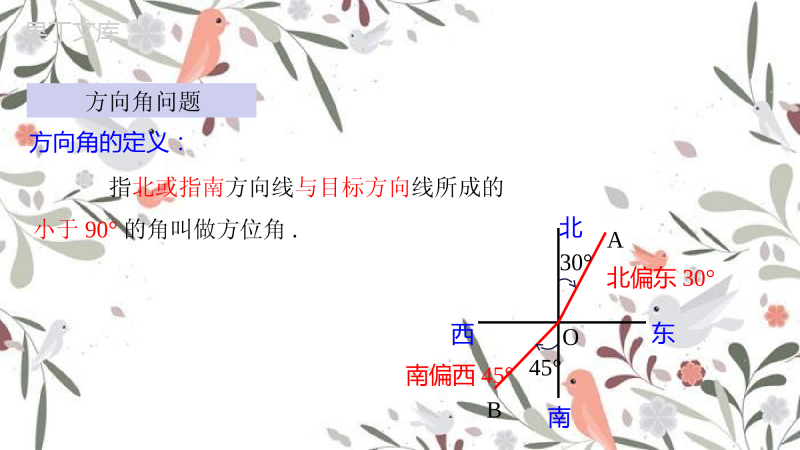
2.5.2解直角三角形的应用2角α值30°45°60°sinαcosαtanα1.在RtABC△中，∠C＝90°，则∠A=___21,7ACBCBAC212.在RtABC△中，∠C=90°,A=60°,AC=∠，则BC的长为＿＿＿33.一辆汽车沿山坡每前进10米，汽车上升米，则山坡的倾斜角α为___度5245α10BCA5230°3ACB∟60°37铅直线水平线视线视线仰角俯角从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.方向角问题方向角的定义：指北或指南方向线与目标方向线所成的小于90°的角叫做方位角.30°45°BOA东西北南北偏东30°南偏西45°某探险者某天到达如图所示的点A处时，他准备估算出离他的目的地——海拔为3500m的山峰顶点B处的水平距离.他能想出一个可行的办法吗？．．AB2、某斜坡的坡度为1:1，则这个斜坡的坡角为.α3l3hABCi1.如图:斜坡AB的坡比是_______3:345°3.若坡角α=60°，则坡度=。3:1例如图所示，一艘渔船以30海里/时的速度由西向东航线.在A处看见小岛C在船北偏东60°方向上，40min后，渔船行驶到B处，此时小岛C在船北偏东30°方向上.已知以小岛C为中心，10海里为半径的范围是多暗礁的危险区.如果这艘渔船继续向东航线，有没有进入危险区的可能.BCA北30°60°解读：方位角：视线与正南（或正北）方向的夹角.思考：如何判断渔船有没有可能进入危险区？如图，如果测得点A的海拔AE为1600m，仰角∠BAC=40°，求A、B两点之间的水平距离AC.（结果保留整数）.利用解直角三角形来解应用问题的一般步骤:(1)审题,画出示意图,并把实际问题转化为数学问题;(2)根据条件,找出已知的元素和需求的元素,并选择合适的边角关系式;(3)求出需求的元素;(4)根据计算结果写出结论.解决与方位角有关的实际问题时，必须先在每个位置中心建立方向标，然后根据方位角标出图中已知角的度数，最后在某个直角三角形内利用锐角三角函数解决问题解答含有方向角问题的方法1.如图，一艘渔船位于灯塔P的北偏东30°方向，距离灯塔18海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东55°方向上的B处，此时渔船与灯塔P的距离约为____海里(结果取整数)．(参考数据：sin55°≈0.8，cos55°≈0.6，tan55°≈1.4)11随堂演练2.如图4-21，一艘船以40km/h的速度向正东航行，在A处测得灯塔C在北偏东60°方向上，继续航行1h到达B处，这时测得灯塔C在北偏东30°方向上.已知在灯塔C的四周30km内有暗礁．问这艘船继续向东航行是否安全？分析：在两个直角三角形中，分别利用300、600角的正切，用同一个参量x表示出AD、BD的长，进而用方程思想求解.C课堂小结今天这节课就到此结束，同学们如果还有其他的问题，请同学们在课下去问老师和其他同学们进行学习，以便可以将这节课的内容融会贯通。