勾股定理的应用2,勾股定理的应用2教案

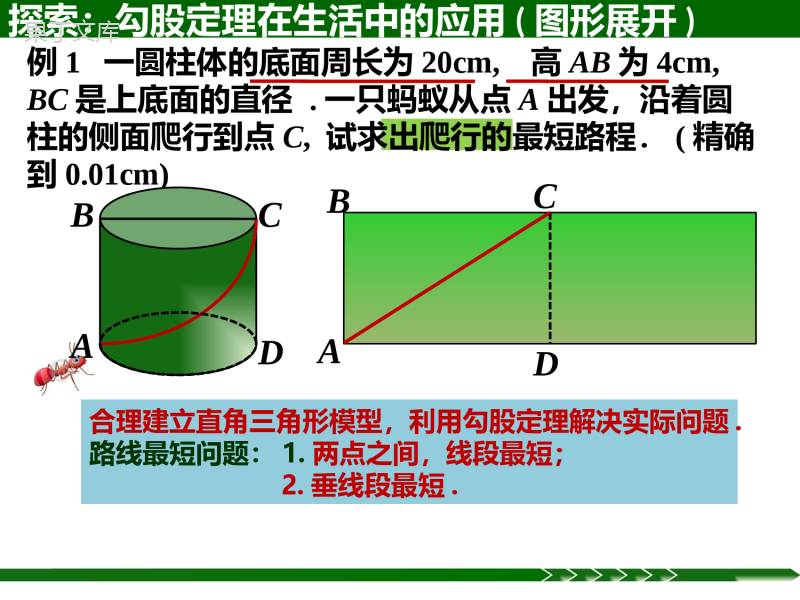
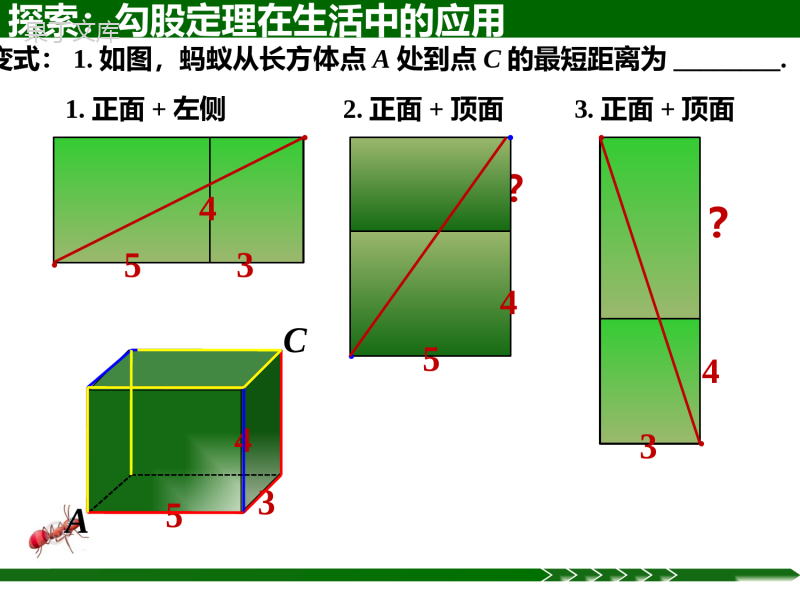
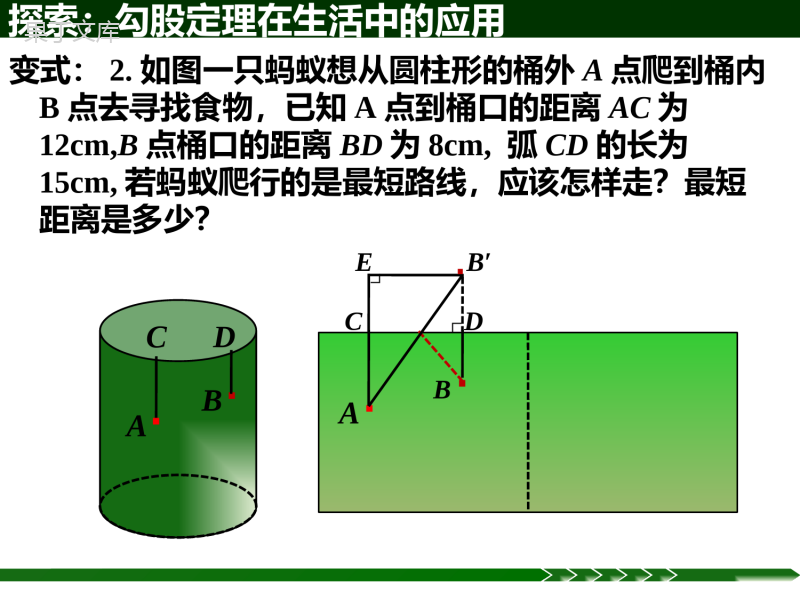
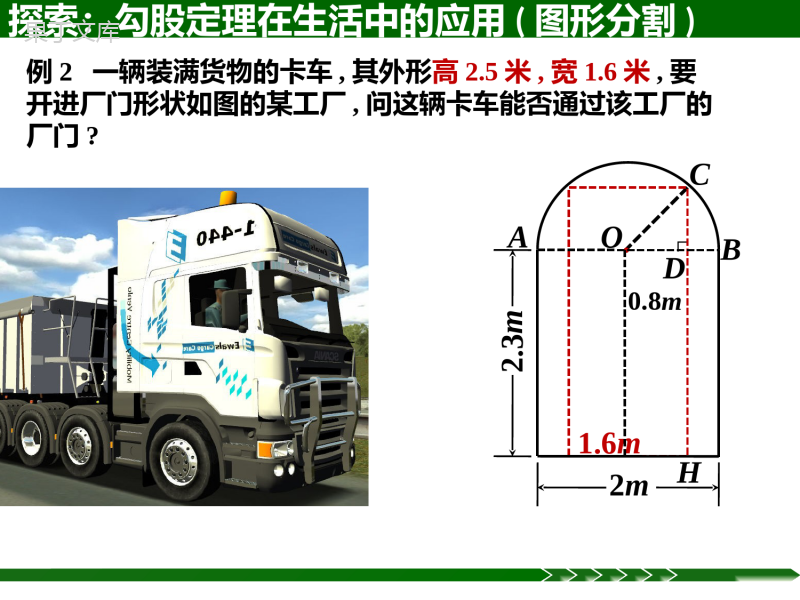
Rt△ABC中，a2+b2=c214.2勾股定理的应用做人启示：在不良交往中颓废；数学启示：这节课告诉你.Rt△ABC中，a2+b2=c2例1一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发，沿着圆柱的侧面爬行到点C,试求出爬行的最短路程．(精确到0.01cm)探索：勾股定理在生活中的应用(图形展开)ABCDDBCA合理建立直角三角形模型，利用勾股定理解决实际问题.路线最短问题：1.两点之间，线段最短；2.垂线段最短.354●●1.正面+左侧AC354变式：1.如图，蚂蚁从长方体点A处到点C的最短距离为________.？54●●2.正面+顶面？34●●3.正面+顶面探索：勾股定理在生活中的应用B·A·CD变式：2.如图一只蚂蚁想从圆柱形的桶外A点爬到桶内B点去寻找食物，已知A点到桶口的距离AC为12cm,B点桶口的距离BD为8cm,弧CD的长为15cm,若蚂蚁爬行的是最短路线，应该怎样走？最短距离是多少？探索：勾股定理在生活中的应用CDB·A·∟EB′∟·∟例2一辆装满货物的卡车,其外形高2.5米,宽1.6米,要开进厂门形状如图的某工厂,问这辆卡车能否通过该工厂的厂门?1.6m●2m2.3m0.8mAOCDBH探索：勾股定理在生活中的应用(图形分割)变式：一辆高３米，宽2.4米的卡车要通过一个半径为3.6米的半圆形隧道，它能顺利通过吗？●OACDB探索：勾股定理在生活中的应用(图形分割)1.2米3.6米∟探索：勾股定理在生活中的应用(图形分割)技巧小结：通过图形的展开，分割拼补等变换，巧妙建立三角形，利用勾股定理解决生活中的实际问题.∟练习121-122第1-2题ABlC5m7m2.轮船A以16海里/时的速度离开港口O向东北方向航行，轮船B在同时同地以12海里/时的速度向西北方向航行.试求A,B两船离开港口O一个半小时后的距离.●O北东南西45°A45°B回顾反思：１、立体图形中路线最短的问题，往往是把立体图形展开，得到平面图形．根据“两点之间，线段最短”确定行走路线，根据勾股定理计算出最短距离．２、在解决实际问题时，首先要画出适当的示意图，将实际问题抽象为数学问题，并构建直角三角形模型，再运用勾股定理解决实际问题．应用勾股定理解决实际问题的一般思路：第2课时勾股定理在数学中的应用建立直角三角形模型1.变式：甲船以每小时30海里的速度，从A处向正北方向航行，同时乙船从A处以每小时40海里的速度向正西方向航行，两小时后，甲、乙两艘轮船相距多少海里？ABC北东南西回顾：勾股定理在生活中的应用能力提高：2.如图，盒内长，宽，高分别是30米，24米和18米，盒内可放的棍子最长是多少米？建立直角三角形模型3.如图,校园内有两棵树,相距12m,一棵树高16m,另一棵树高11m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少距离?ADCB∟E建立直角三角形模型例3如图，在3×3的正方形网格中，每个小正方形的边长都为1，请在给定网格中按下列要求画出图形：(1)画出所有从从点A出发，另一个端点Ｂ在格点(即小正方形的顶点)上，且长度为√5的线段；(2)画出所有以(1)中所画线段为腰的等腰三角形．●A技巧小结：1.把握特征；2.注意分类.BCDE建立直角三角形模型△ABC是直角三角形吗？S△ABC=_______.巧寻直角三角形：例4.如图，已知CD＝６m,AD＝８m，∠ADC＝90°,BC＝24m,AB＝26m．求图中阴影部分的面积．ADBC∟练习123页1-2题1.注意分类；2.画长度为√3cm和√5cm的线段注意建立三角形.3.已知：等边△ABC的边长是6cm(1)求高AD的长.(2)求S△ABC.ABDC∟4.等腰三角形底边上的高为8，周长为32，这个三角形的面积为_____.∟5.如图,在△ABC中,AB＝AC＝5,BC＝6,若点P在边AC上移动,则BP的最小值是_____．5.如图所示，已知四边形ABCD中，∠A＝∠BCD＝90°，∠ABC＝45°，AD＝1，AB＝4，试求四边形ABCD的面积．∟∟BACDE6.如图，居民楼A与马路l相距60米，一辆载重汽车在马路l上以36千米/时的速度行驶，在距A点100米的点P处就可使居民楼受到噪音影响，求这辆汽车给A楼的居民带来多长时间的噪音影响？7.如图，在长方形纸片ABCD中，AB＝8cm，把长方形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，若AF＝254cm，则AD的长为()A．4cmB．5cmC．6cmD．7cm7.如图，在长方形纸片ABCD中，AB＝8cm，把长方形纸片沿直线AC折叠，点B落在点E处，AE交DC于点F，若AF＝254cm，则AD的长为()A．4cmB．5cmC．6cmD．7cm课堂小结：(1)非直角三角形的计算往往需要作辅助线构造直角三角形，然后用勾股定理来解决．如等腰三角形、等边三角形的计算，作高是构造直角三角形的重要手段．(2)运用勾股定理计算时要学会灵活变形，还常常与平方差公式和两数和(差)的平方公式结合使用，比如C＝A2＋B2，A2＝C2－B2＝(C＋B)(C－B)，C2＝A2＋B2＝(A＋B)2－2AB，C2＝A2＋B2＝(A－B)2＋2AB等．(1)非直角三角形的计算往往需要作辅助线构造直角三角形，然后用勾股定理来解决．如等腰三角形、等边三角形的计算，作高是构造直角三角形的重要手段．(2)运用勾股定理计算时要学会灵活变形，还常常与平方差公式和两数和(差)的平方公式结合使用，比如C＝A2＋B2，A2＝C2－B2＝(C＋B)(C－B)，C2＝A2＋B2＝(A＋B)2－2AB，C2＝A2＋B2＝(A－B)2＋2AB等．课后作业：1.课本123页：14.2第1-5题2.完成练习册本课时的习题.让别人因为你的存在而幸福.挑战题：如图，在锐角三角形ABC中,AB＝4√2,∠BAC＝45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,求BM＋MN的最小值是.CBDANM8．如图，一个圆柱体的底面周长为ccm，在圆柱体的表面用一根长为lcm的彩色带子由A点到B点缠紧(A，B两点都在圆柱体的轴截面上)，那么这个圆柱体的高可表示为________cm.方法技能：求最短路程常用的方法有：1．根据“两点之间，线段最短”求最短路程；2．利用“垂线段最短”求最短路程；3．利用轴对称求最短路程；4．利用立体图形的平面展开图求最短路程．易错提示：实际问题常以文字叙述，而非以数学语言表达，所以将文字叙述转化为图形中的等量关系时不要出错．