相似三角形判定定理的证明(课件)-2022-2023学年九年级数学上册同步精品课堂(北师大版)

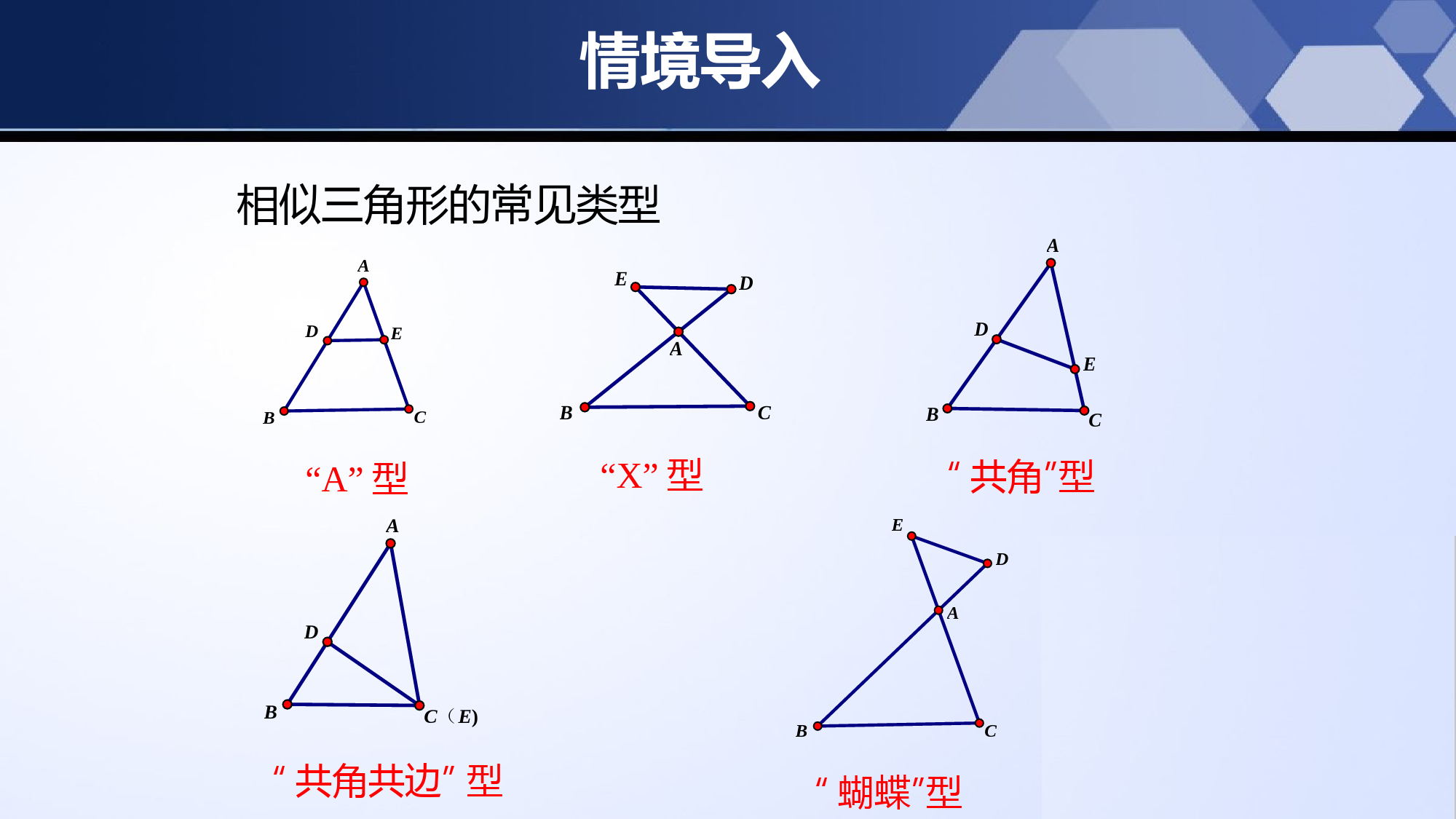
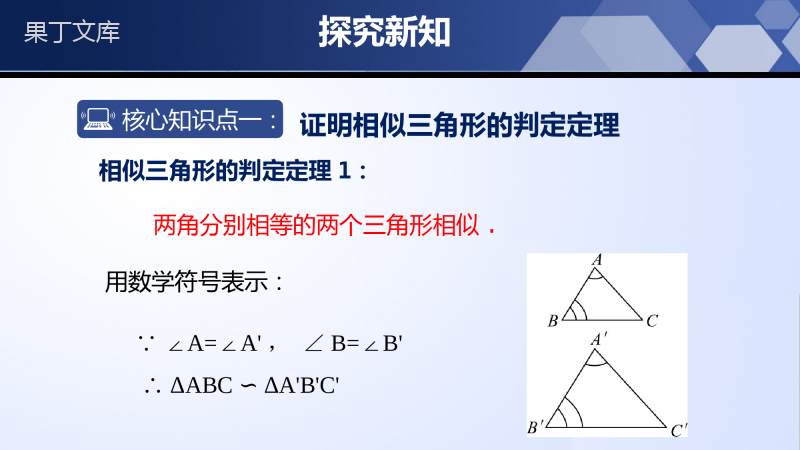
新课标北师大版九年级上册4.5相似三角形判定定理的证明第四章图形的相似学习目标1．了解相似三角形判定定理的证明过程，知道构造全等三角形是一种有效的证明方法．2．进一步掌握相似三角形的三个判定定理．情境导入两角对应相等，两三角形相似.三边对应成比例，两三角形相似.相似三角形的判定方法:两边对应成比例且夹角相等，两三角形相似.在上一节中，我们探索了三角形相似的条件，本节我们将对它们进行证明.情境导入相似三角形的常见类型“A”型“X”型“共角”型“共角共边”型“蝴蝶”型ABCDEAEDBCABCDEABC（E)DADBCE探究新知核心知识点一：证明相似三角形的判定定理两角分别相等的两个三角形相似.用数学符号表示：∵∠A=A'∠，∠B=B'∠∴ΔABCΔA'B'C'∽相似三角形的判定定理1：探究新知已知：如图，△ABC和△A′B′C′中，∠A=∠A′，∠B=∠B′，ABCA′B′C′求证：△ABC∽△A'B'C'DE证明：在△ABC的边AB（或它的延长线）上截取AD＝A′B′，过点D作BC的平行线，交AC于点E，则∠ADE＝∠B，∠AED＝.ADAEABAC探究新知FABCA′B′C′DE过点D作AC的平行线，交BC于点F，.ABADCFCB则.AECFACCB∵DE∥BC，DF∥AC，∴四边形DFCE是平行四边形.∴DE＝CF..AEDEACCB.ADAEDEABACBC而∠ADE＝∠B，∠DAE＝∠BAC，∠AED＝∠C∴△ADE∽△ABC∵∠A＝∠A′，∠ADE＝∠B＝∠B′，AD＝A′B′∴△ADE△A′B′C′∴△ABC∽△A'B'C'探究新知两边成比例且夹角相等的两个三角形相似用数学符号表示：∵∠A=A'∠，∴ΔABCΔA'B'C'∽.''''ABACABAC相似三角形的判定定理2：探究新知ABCA′B′C′求证：△ABC∽△A'B'C'DE证明：在△ABC的边AB（或它的延长线）上截取AD＝A′B′，过点D作BC的平行线，交AC于点E，则∠B＝∠ADE，∠C＝∠AED，已知：如图，△ABC和△A′B′C′中，∠A=∠A′，.ABACABAC∴△ABC∽△ADE探究新知.ABACADAE,,ABACADABABAC.ABACADAC.ACACAEACAEAC而∠A＝∠A′，∴△ADE≌△A′B′C′∴△ABC∽△A'B'C'ABCA′B′C′DE探究新知三边成比例的两个三角形相似用数学符号表示：∴△ABC∽△A1B1C1111111CBBCCAACBAAB∵ABCA1B1C1相似三角形的判定定理3：探究新知ABCA′B′C′求证：△ABC∽△A'B'C'DE证明：在△ABC的边AB（或它的延长线）上截取AD＝A′B′，AE＝A′C′连接DE.已知：如图，△ABC和△A′B′C′中，=.ABBCACABBCAC,,,ABACADABAEACABAC.ABACADAE探究新知ABCA′B′C′DE而∠BAC＝∠DAE，∴△ABC∽△ADE.ABBCADDE,,ABBCADABABBC又.ABBCADBC.BCBCDEBC.DEBC∴△ADE≌△A′B′C′∴△ABC∽△A'B'C'探究新知判断两个三角形相似，常有以下几种形式：有一个公共角：ACD=ABC时△ACD∽△ABCAED=ABC时△AED∽△ABCDE//BC时△ADE∽△ABCABCABCCBADEDED有一对对顶角：ADE=ACB时△ADE∽△ACBDE//BC时△ADE∽△ABCAAEDBCEDBC归纳总结探究新知一线三等角：1=2=3时△ABD∽△BCE321FBACDE1=2=3时△ABE∽△CDB321EDABC注意：一线三等角的一种特殊情况是∠1=2=3=90°∠∠判断两个三角形相似，常有以下几种形式：归纳总结探究新知核心知识点二：相似三角形判定定理的运用1．在△ABC与△A′B′C′中，有下列条件：①ABA′B′＝BCB′C′；②BCB′C′＝ACA′C′；∠A＝∠A′；④∠C＝∠C′.如果从中任取两个条件组成一组，那么能判断△ABC∽△A′B′C′的共有()A．1组B．2组C．3组D．4组C探究新知2．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试证明：△ABF∽△EAD.证明：∵矩形ABCD中，AB∥CD，∠D＝90°，∴∠BAF＝∠AED.∵BF⊥AE，∴∠AFB＝90°.∴∠AFB＝∠D，∴△ABF∽△EAD.探究新知3.已知，如图，D为△ABC内一点，连接BD、AD，分析：由已知条件∠ABD＝∠CBE，∠DBC公用，所以∠DBE＝∠ABC，要证的△DBE和△ABC，有一对角相等，要证两个三角形相似，可再找一对角相等，或以BC为边在△ABC外作∠CBE＝∠ABD，∠BCE＝∠BAD，连接DE.求证：△DBE∽△ABC.者找夹这个角的两边对应成比例．从已知条件中可看到△CBE∽△ABD，这样既有相等的角，又有成比例的线段，问题就可以得到解决．探究新知证明：在△CBE和△ABD中，∠CBE＝∠ABD，∠BCE＝∠BAD，∴△CBE∽△ABD，∴BCAB＝BEBD，即：BCBE＝ABBD.在△DBE和△ABC中，∠CBE＝∠ABD，∴∠CBE＋∠DBC＝∠ABD＋∠DBC，BCBE＝ABBD.∴△DBE∽△ABC.∴∠DBE＝∠ABC且随堂练习1．下列命题中是真命题的是()A．有一个角相等的直角三角形都相似B．有一个角相等的等腰三角形都相似C．有一个角是120°的等腰三角形都相似D．两边成比例且有一角相等的三角形都相似C随堂练习2．如图，在平行四边形ABCD中，点E在AD边上，连接CE并延长，与BA的延长线交于点F，若AE＝2ED，CD＝3cm，则AF的长为()A．5cmB．6cmC．7cmD．8cmB随堂练习413．如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC=BC．图中相似三角形共有（）A．1对B．2对C．3对D．4对C随堂练习4．如图，在▱ABCD中，AB＝10，AD＝6，点E是边AD的中点，在AB上取一点F，使△CBF与△CDE相似，则BF的长是_______．1.8随堂练习解：∵∠A=∠A,∠ABD=∠C,∴△ABD∽△ACB,∴AB:AC=AD:AB,∴AB2=AD·AC.∵AD=2,AC=8,∴AB=4.5.已知：如图,∠ABD=∠C，AD=2,AC=8，求AB.随堂练习6．如图，D是△ABC的边BC上的一点，AB＝2，BD＝1，DC＝3，求证：△ABDCBA.∽△证明：∵AB＝2，BD＝1，DC＝3，∴AB2＝4，BD·BC＝1×(1＋3)＝4.∴AB2＝BD·BC.即ABBC＝BDBA.而∠ABD＝∠CBA.∴△ABD∽△CBA.课堂小结一、相似三角形判定定理的证明1.两角对应相等，两三角形相似.3.两边对应成比例且夹角相等,两三角形相似.二、相似三角形判定定理的应用2.三边对应成比例,两三角形相似.谢谢~