八上华东师大版数学14.1勾股定理

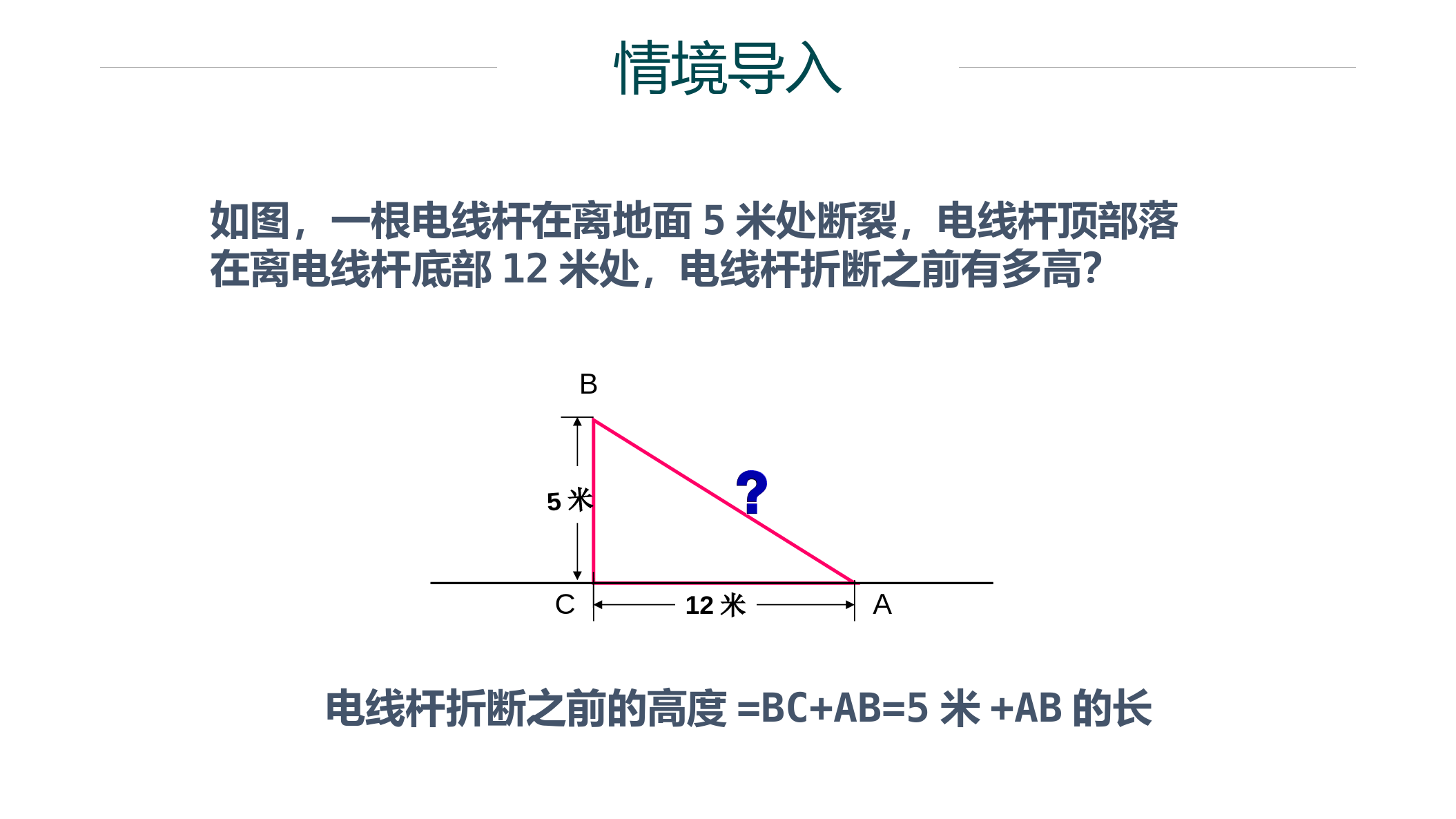
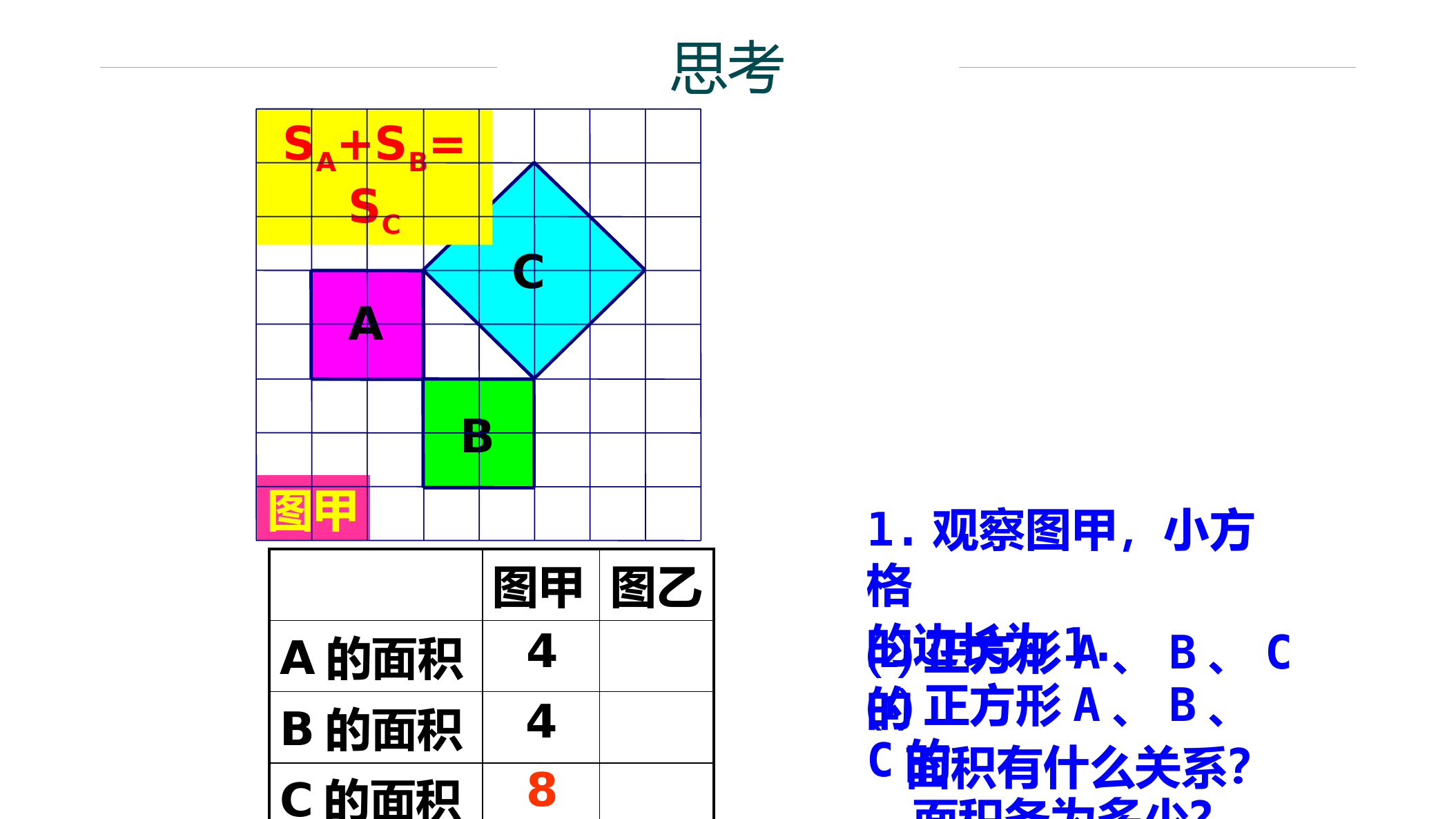
华东师大版14.1勾股定理导入与思考1探究与证明2回顾与练习3目录CONTENTS导入与思考•情境导入•思考01章节PART情境导入如图，一根电线杆在离地面5米处断裂，电线杆顶部落在离电线杆底部12米处，电线杆折断之前有多高？5米BAC12米电线杆折断之前的高度=BC+AB=5米+AB的长图甲图乙A的面积B的面积C的面积448C1.观察图甲，小方格的边长为1.⑴正方形A、B、C的⑵正方形A、B、C的面积有什么关系？ABCSA+SB=SC图甲思考2.观察图乙，小方格的边长为1.⑴正方形A、B、C的91625⑵正方形A、B、C的448图甲图乙A的面积B的面积C的面积ABCSA+SB=SC图甲ABCC图乙SA+SB=SC思考思考ABC图乙2.观察图乙，小方格的边长为1.91625SA+SB=SC⑵正方形A、B、C的448ABCSA+SB=SC图甲图甲图乙A的面积B的面积C的面积abcabc思考ABCC图乙SA+SB=SCSA+SB=SC图甲abcabc3.猜想a、b、c之间的关系？a2+b2=c2探究与证明•合作探究•理论证明•趁热打铁02章节PART合作探究小组活动：请你利用自己准备的四个全等的直角三角形拼出以斜边为边长的正方形证明aaaabbbbcccc大正方形的面积可以表示为________；也可以表示为___________.(a+b)2c2+4·∵(a+b)2=c2+4·a2+2ab+b2=c2+2ab∴a2+b2=c2结论如果直角三角形两直角边分别为a，b，斜边为c，那么即直角三角形两直角边的平方和等于斜边的平方222cbaac勾弦b股勾股定理（毕达哥拉斯定理）笔记勾股定理：如果直角三角形两直角边分别为a，b，斜边为c，有a2+b2=c2逆定理：如果三角形的三边长a、b、c满足，那么这个三角形是直角三角形。a2+b2=c2反过来结论判断由线段a，b，c组成的三角形是不是直角三角形?(1)a=15，b=17，c=8;(2)a=13，b=15，c=14解:(1)最大边为17∵152+82=225+64=289172=289∴152+82=172∴以15,8,17为边长的三角形是直角三角形(2)最大边为15∵132+142=169+196=365152=225∴132+142≠152∴以13,15,14为边长的三角形不是直角三角形像15,17,8,能够成为直角三角形三条边长的三个正整数，称为勾股数.趁热打铁回顾与练习03章节PART∴电线杆折断之前的高度=BC+AB=5米+１３米＝１８米5米BAC12米解：∵ＢＣ⊥ＡC，∴在Ｒt△ＡＢＣ中，ＡＣ＝１２，ＢＣ＝５,根据勾股定理，22222212516913ABACBCABAB即回顾如图，一根电线杆在离地面5米处断裂，电线杆顶部落在离电线杆底部12米处，电线杆折断之前有多高？练习勾股定理另一种证法1.设直角三角形的两条直角边分别为a,b,斜边长为c.(1)已知a=6,c=10,求b:(2)已知a=5,b=12,求c:(3)已知c=25,b=15,求a.【答案】(1)8；(2)13；(3)20【解析】直接利用勾股定理，己知两边求第三边2.图①是用硬纸板做成的两个完全一样的直角三角形，两直角边长分别为α和b,斜边长为c,图②是以c为直角边的等腰直角三角形，请你开动脑筋，将它们拼成一个能证明勾股定理的图形(1)画出拼成的这个图形的示意图，指出它是什么图形：(2)用这个图形证明勾股定理：(3)假设图①中的直角三角形有若干个，你能运用图①中所给的直角三角形拼出另一组能证明勾股定理的图形吗？请画出拼后的示意图。S梯形=(a+b)(a+b),S梯形=2SADE△+SABE△=2•ab+c2,化简得证a2+b2=c2练习3.如图，等腰三角形ABC底边上的高AD为4cm，周长为16cm，则△ABC的面积是()A．14cm2B．13cm2C．12cm2D．8cm2C练习4．如图，在RtABC△中，∠C＝90°，若a＋b＝14，c＝10，求RtABC△的面积．解：∵∠C＝90°，∴a2＋b2＝c2＝100.∴(a＋b)2－2ab＝100.∴142－2ab＝100.∴ab＝48.∴SABC△＝ab＝24.练习5.如图，将矩形ABCD沿EF折叠，使点D与点B重合，己知AB=3,AD=9,求BE的长。【答案】BE=5【解析】设BE=x,则DE=BE=x,AE=AD-DE=9-x.在RtABE△中，AB2+AE2=BE2∴32+(9-x)2=x2,解得x=5.练习6.如图，有两棵树，一棵高8米，另一棵高2米，两树相距8米，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少要飞米。【答案】10.【解析】根据两点之间线段最短的定理，准确的作出小鸟从一棵树的树梢飞到另一棵树的树梢的路线为最短距离的图形，构造RtABC,△根据勾股定理即可。因为BE=DC=2,AE=8,BC=8,AB=AE-BE=6,在RABC△中，AC==10,所以小鸟飞的最短距离为10米。THANKYOU