从勾股定理谈起,从勾股定理谈起盛立人

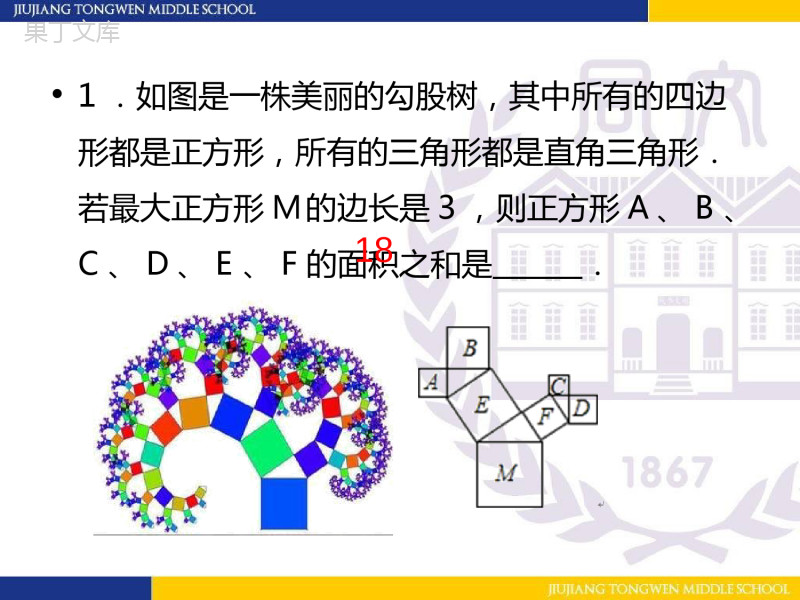
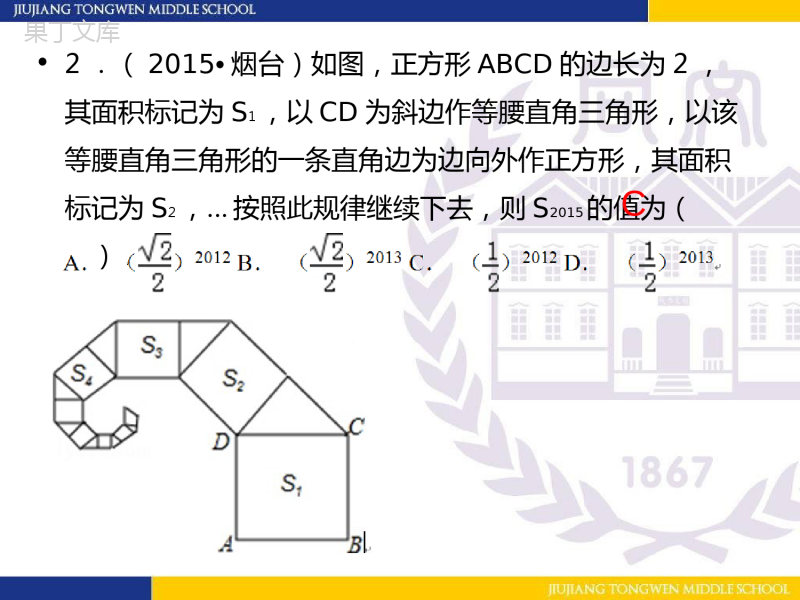
•毕达哥拉斯(Pythagoras，约公元前580~约前500)古希腊数学家、哲学家。一、毕达哥拉斯——毕达哥拉斯树从勾股图出发，通过迭带可得到枝繁叶茂、栩栩如生的毕达哥拉斯树（勾股数）。•1．如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若最大正方形M的边长是3，则正方形A、B、C、D、E、F的面积之和是．18•2．（2015•烟台）如图，正方形ABCD的边长为2，其面积标记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2，…按照此规律继续下去，则S2015的值为（）.C•3.在直线上依次摆放着七个正方形（如图3所示）。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是SS12、•解：∵∠ACB+ECD=90°∠，∠DEC+ECD=90°ACB=DE∠∴∠∠C•∵∠ABC=CDE∠，AC=CE，•在△ABC和△CDE中，∴△ABCCDE≌△（AAS），∴BC=DE•∴（如上图），根据勾股定理的几何意义，•b的面积=a的面积+c的面积•3.在直线上依次摆放着七个正方形（如图3所示）。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是SS12、4•4.勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为多少？OP•解：如图，延长AB交KF于点O，延长AC交GM于点P，则四边形OALP是矩形．•∵∠CBF=90°，∴∠ABC+OBF=90°∠，•又∵直角△ABC中，∠ABC+ACB=90°∠，∴∠OBF=ACB∠，•在△OBF和△ACB中，，∴△OBFACB≌△（AAS），∴AC=OB，•同理：△ACBPGC≌△，∴PC=AB，∴OA=AP，所以，矩形AOLP是正方形，•边长AO=AB+AC=3+4=7，所以，KL=3+7=10，LM=4+7=11，•因此，矩形KLMJ的面积为10×11=110．•1.(河北)如图是甲、乙两张不同的矩形纸片，将它们分别沿着虚线剪开后，各自要拼一个与原来面积相等的正方形，则（）•A．甲、乙都可以•B．甲、乙都不可以•C．甲不可以、乙可以•D．甲可以、乙不可以A•赵爽，中国古代数学家。东汉末至三国时代吴国人。•为《周髀算经》作注，代表作：《勾股圆方图注》。•赵爽的这个证明可谓别具匠心，极富创新意识。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系。二、赵爽——赵爽弦图•2．（2015•遵义）我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1））．图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3．若正方形EFGH的边长为2，则S1+S2+S3=．12•3．（2015•株洲改编）如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果大正方形的面积是25，小正方形的面积是1，直角三角形的两直角边分别是a和b，那么（a+b）2的值为________．49•4.长方形ABCD中被嵌入了如图所示6个相同的正方形,其中每边各有一个正方形顶点落在上面。已知AB=22厘米,BC=20厘米,那么每一个正方形的面积为________平方厘米。,()()b,3222:320abABabBC每个小正方形中切割成的四个小直角三角形的长边图中红色线段为a,短边图中蓝色线段为则226240.abab每个正方形的面积为40•刘徽（约公元225年—295年），魏晋期间伟大的数学家，中国古典数学理论的奠基人之一。是中国数学史上一个非常伟大的数学家，他的杰作《九章算术注》和《海岛算经》是中国最宝贵的数学遗产。三、刘徽——青朱出入图•勾股定理——画家证法。达·芬奇：欧洲文艺复兴时期的天才科学家、发明家、画家。•1.（2013北京）阅读下面材料：•小明遇到这样一个问题：如图1，在边长为a(a>2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠CHN=∠DEP=45°时，求正方形MNPQ的面积。•小明发现：分别延长QE，MF，NG，PH，交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形（如图2）•（1）若将上述四个等腰直角三角形拼成一个新的正方形（无缝隙，不重叠），则这个新的正方形的边长为_____；•（2）求正方形MNPQ的面积。a1441122AERMNPQSS正方形•参考小明思考问题的方法，解决问题：•如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ，若，则AD的长为__________。33RPQS2313332223ADAD得MNF,,,3,MNFABCPRQADMMRFDPNQEKSSSS如图可证明这三个等腰三角形拼成边长为a的等边三角形可得所以•2.（2014•博野县模拟）如图，Rt△ABC中，∠C=90°，AC=3，BC=4．分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，四块阴影部分的面积分别为S1、S2、S3、S4．则S1+S2+S3+S4等于（）•解：图中S4阴影部分全等于Rt△ABC．•S3与△FPT全等，所以S1+S3也等于Rt△ABC．•S2的左上方的顶点为F，过F作AM的垂线交AM于D，可证明Rt△ADF≌Rt△ABC，而图中Rt△DFK全等于①，•所以S2=Rt△ABC．•S1+S2+S3+S4•=（S1+S3）+S2+S4•=Rt△ABC的面积+Rt△ABC的面积+Rt△ABC的面积•=Rt△ABC的面积×3•=4×3÷2×3•=18通过这节课的学习：•你都学到了些什么？•让你感触最深的是什么？•有哪些地方还是让你感到疑惑的？•你还想知道有关勾股定理的其它的证法吗？作业•查阅还有哪些勾股定理的证明方法。•你能不能自己也去画一画、拼一拼，设计一种方案去验证勾股定理？