三角形内角和定理(第2课时)-2022-2023学年八年级数学上册同步教材教学精品课件(北师大版)

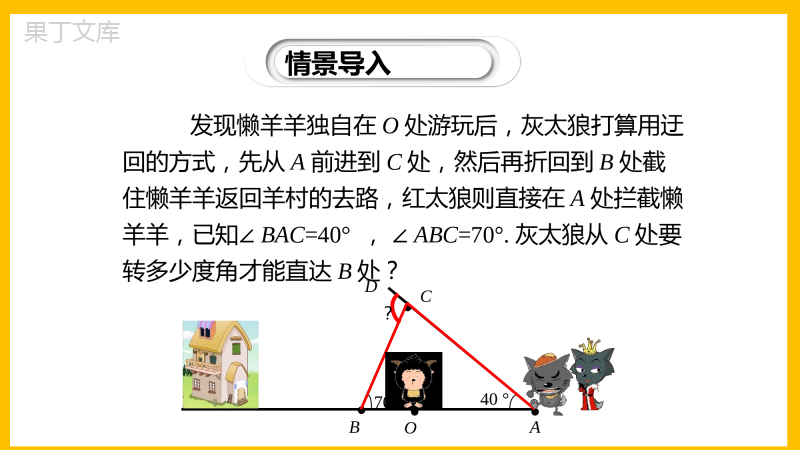
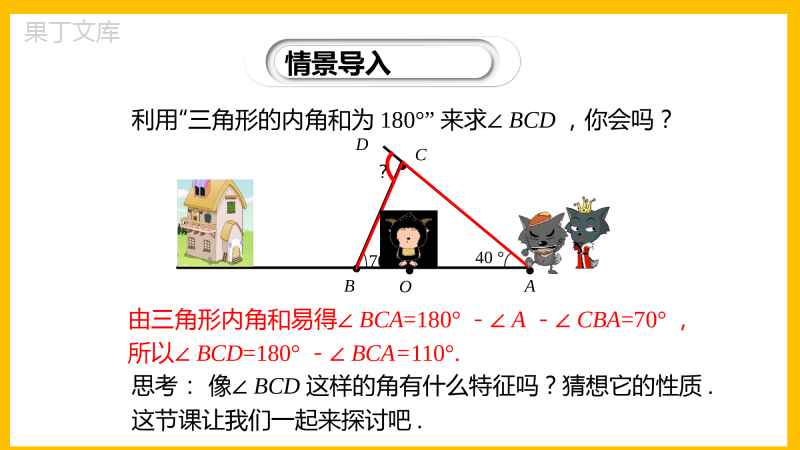
第七章平行线的证明7.5.2三角形内角和定理（第2课时）北师版数学八年级上册学习目标1．掌握三角形内角和定理的两个推理，并能运用这些定理解决简单的问题．2．经历探索与证明的过程，进一步发展推理能力．3．在一题多解、一题多变中，积累解决几何问题的经验，提升解决问题的能力．情景导入BDCAO●40°70°？●●●发现懒羊羊独自在O处游玩后，灰太狼打算用迂回的方式，先从A前进到C处，然后再折回到B处截住懒羊羊返回羊村的去路，红太狼则直接在A处拦截懒羊羊，已知∠BAC=40°，∠ABC=70°.灰太狼从C处要转多少度角才能直达B处？情景导入利用“三角形的内角和为180°”来求∠BCD，你会吗？思考：像∠BCD这样的角有什么特征吗？猜想它的性质.这节课让我们一起来探讨吧.BDCAO●40°70°？●●●由三角形内角和易得∠BCA=180°－∠A－∠CBA=70°，所以∠BCD=180°－∠BCA=110°.探索新知三角形的外角的概念一观察下面一组图形中∠1在各个图形中的位置，你能发现它们的共同特征吗？1.1∠的顶点在三角形的一个顶点上;2.1∠的一条边是三角形的一条边;3.1∠的另一条边是三角形的某条边的延长线.探索新知外角的定义：△ABC内角的一条边与另一条边的反向延长线组成的角，称为△ABC的外角.ABCD（1）顶点在三角形的一个顶点上.如：∠ACD的顶点C是△ABC的一个顶点；（2）一条边是三角形的一边.如：∠ACD的一条边AC是△ABC的一条边；（3）另一条边是三角形某条边的延长线.如：∠ACD的边CD是△ABC的BC的延长线.探索新知ABCD你能画出△ABC的其他外角吗？每一个三角形都有6个外角．每一个顶点相对应的外角都有2个，且这2个角为对顶角.探索新知三角形的外角的性质二问题1：如图，△ABC的外角∠BCD与其相邻的内角∠ACB有什么关系？∠BCD与∠ACB互补.三角形的外角ACBD相邻的内角不相邻的内角探索新知问题2：如图，△ABC的外角∠BCD与其不相邻的两内角(∠A、∠B)有什么关系？∠A+∠B=∠BCD三角形的外角ACBD相邻的内角不相邻的内角探索新知D证明：过C作CEAB∥，ABC12∴∠1=∠B，（两直线平行，同位角相等）∠2=∠A，（两直线平行，内错角相等）∴∠ACD=1+2=∠∠∠A+∠B.E已知：如图，△ABC，求证：∠ACD=∠A+∠B.总结归纳探索新知三角形内角和定理的推论（一）ABCD(((三角形的一个外角等于和它不相邻的两个内角的和.几何语言：∵∠ACD是△ABC的一个外角∴∠ACD=∠A+∠B.探索新知例1已知，如图，在△ABC中，∠B=∠C，AD平分外角∠EAC．求证：AD∥BCBACDE证明：∵∠EAC=∠B+∠C（三角形的一个外角等于和它不相邻的两个内角的和）∠B=∠C（已知）∴∠B=∠EAC（等式的性质）∵AD平分∠EAC（已知）∴∠DAE=∠EAC（角平分线的定义）∴∠DAE=∠B（等量代换）∴AD∥BC（同位角相等，两直线平行）21212121探索新知探究：如图，试比较∠2、∠1的大小；如图，试比较∠3、∠2、∠1的大小.图图解：∵∠2=1+∠∠B,∴∠2＞∠1.解：∵∠2=1+∠∠B,∠3=2+∠∠D,∴∠3＞∠2＞∠1.BCEDAACBD探索新知总结归纳三角形内角和定理的推论（二）三角形的一个外角大于任何一个与它不相邻的内角.∵∠1是△ABC的外角∴∠1＞∠B，∠1＞∠C几何语言：ABC1探索新知例2如图，P是△ABC内的一点，求证：∠BPC＞∠A.证明：延长BP,交AC于D，∵∠BPC是△PDC的外角(外角定义)∴∠BPC＞∠PDC(三角形的一个外角大于任何一个和它不相邻的内角)．∵∠PDC是△ABD的外角(外角定义)∴∠PDC＞∠A(三角形的一个外角大于任何一个和它不相邻的内角)．∴∠BPC＞∠A.证明：∵∠1+BAF=180°∠∠2+CBD=180°∠∠3+ACE=180°(∠平角的定义)∴∠1+2+3+BAF+CBD+ACE=3×180°∠∠∠∠∠又∵∠1+2+3=180°(∠∠三角形内角和定理)∴∠BAF+CBD+ACE=540°-180°∠∠∠BAF+CBD+ACE=360°∠∠已知：∠BAF，∠CBD，∠ACE是△ABC的三个外角．求证：∠BAF+CBD+ACE=360°.∠∠定理3.三角形三个外角的和是360°1BC23FEAD探索新知探索新知注意：在这里,我们通过三角形的内角和定理直接推导出两个新定理.像这样,由一个基本事实或定理直接推出的定理,叫做这个基本事实或定理的推论.推论可以当做定理使用.总结归纳当堂检测1.判断下列命题的对错.（1）三角形的外角和是指三角形的所有外角的和.（）（2）三角形的外角和等于它的内角和的2倍.（）（3）三角形的一个外角等于两个内角的和.（）（4）三角形的一个外角等于与它不相邻的两个内角的和.（）（5）三角形的一个外角大于任何一个内角.（）（6）三角形的一个内角小于任何一个与它不相邻的外角.（）当堂检测2.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.无法确定C3.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于()A.120°B.115°C.110°D.105°BFEDCBA当堂检测4.如图，∠A，∠1，∠2的大小关系是()A．∠A＞∠1＞∠2B．∠2＞∠1＞∠AC．∠A＞∠2＞∠1D．∠2＞∠A＞∠1B当堂检测5.如图，射线AD，BE，CF构成∠1，∠2，∠3，则∠1＋∠2＋∠3等于()A．180°B．360°C．540°D．无法确定B当堂检测6.如图：在△ABC中，∠BAC＝90°，AD⊥BC于点D，点E是AD上一点．求证：∠BED>∠C.解：∵∠BAC＝90°(已知)，∴∠1＋∠2＝90°，∵AD⊥BC(已知)，∴∠C＋∠2＝90°，∴∠1＝∠C（等式的性质），∵∠BED>1∠(已知)，∴∠BED>∠C.12当堂检测4、如图，∠A=51°，∠B=20°，∠C=30°，求∠BDC的度数.ABCD((20°30°解法一：连接AD并延长于点E.在△ABD中，∠1+∠ABD=3∠，在△ACD中，∠2+∠ACD=4.∠因为∠BDC=3+4∠∠，∠BAC=1+2∠∠，所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.E))12)3)4当堂检测ABCD(((51°20°30°E)1解法二：延长BD交AC于点E.在△ABE中，∠1=∠ABE+∠BAE，在△ECD中，∠BDC=1+∠∠ECD.所以∠BDC=∠BAC+∠ABD+∠ACD=51°+20°+30°=101°.解法三:连接延长CD交AB于点F（解题过程同解法二）.)2F定理1.三角形的一个外角等于和它不相邻的两个内角的和定理2.三角形的一个外角大于任何一个和它不相邻的内角定理3.三角形三个外角的和是360°