统计图的选择-2022-2023学年七年级数学上册教材配套教学课件(北师大版)

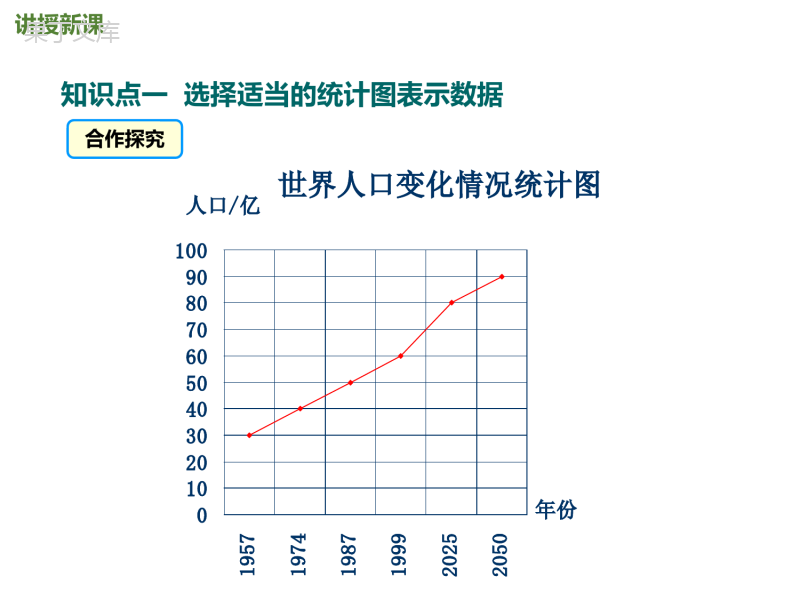
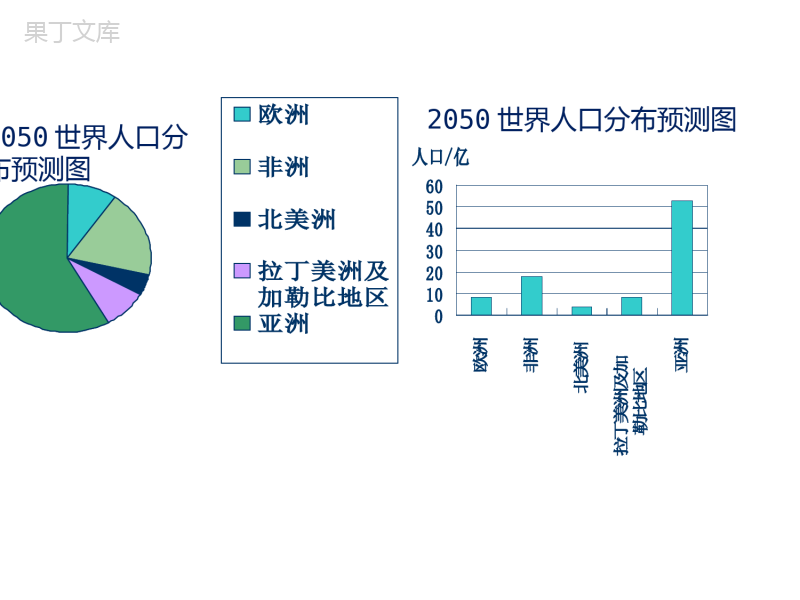
第六章数据的收集与整理6.4统计图的选择北师大版七年级上册新课导入讲授新课当堂检测课堂小结学习目标1、掌握不同统计图的特点，学会根据题目的条件选取合适的统计图来表示数据的趋势；2、根据题目中所给的数据，画出合适的统计图，从而根据统计图做出正确的决策；温故知新条形统计图：用一个单位长度表示一定的数量，根据数量的多少画成长短不同的直条，然后把这些直条按一定的顺序排列起来。折线统计图：以折线的上升或下降来表示统计数量的增减变化的统计图。扇形统计图一般指扇形图。扇形图，又称扇形统计图，它是用整个圆表示总数，用圆内各个扇形的大小表示各部分数量占总数的百分数。通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系。讲授新课知识点一选择适当的统计图表示数据合作探究世界人口变化情况统计图0102030405060708090100195719741987199920252050年份人口/亿世界人口变化情况统计图0102030405060708090100195719741987199920252050年份人口/亿欧洲非洲北美洲拉丁美洲及加勒比地区亚洲2050世界人口分布预测图0102030405060欧洲非洲北美洲拉丁美洲及加勒比地区亚洲人口/亿2050世界人口分布预测图欧洲非洲北美洲拉丁美洲及加勒比地区亚洲0102030405060欧洲非洲北美洲拉丁美洲及加勒比地区亚洲人口/亿根据上图，回答下列问题：（1）三幅统计图分别表示了什么内容？（2）从哪幅统计图中你能看出世界人口的变化情况？（3）2050年非洲人口大约将达到多少亿？你是从哪幅图中得到这个数据的？（4）2050年亚洲人口比其他各洲的人口总和还要多，你从哪幅图中可以明显地得到这个结论？（5）比较三种统计图的特点，并与同伴进行交流.总结归纳条形统计图能清晰地表示出每个项目的具体数目及之间的大小关系.折线统计图能够清晰地反映同一事物在不同时期的变化情况.扇形统计图能清晰地表示各部分在总体中所占的百分比及之间的大小关系.典例精析例1：某中学七年级(1)班共有学生40人，该班开设了排球、篮球和足球三项体育兴趣课，要求每个学生必须参加，且只能参加其中一项球类运动，图①是该班学生报名后，小明同学经统计而绘制成的条形统计图的一部分．(1)请你帮小明同学把条形统计图补充完整；(2)请你根据条形统计图中的数据，改用扇形统计图表示出来(如图②)；解：(1)参加排球兴趣课的有：40－20－12＝8(人)，如图.(2)从条形统计图可知，参加足球兴趣课的有20人，占总人数的百分比为20÷40×100%＝50%，所在扇形圆心角的度数为360°×50%＝180°；参加排球兴趣课的有8人，占总人数的百分比为8÷40×100%＝20%，所在扇形圆心角的度数为360°×20%＝72°；参加篮球兴趣课的有12人，占总人数的百分比为12÷40×100%＝30%，所在扇形圆心角的度数为360°×30%＝108°，扇形统计图如图②.足球50%排球50%篮球30%知识点二利用统计图准确表示事物的某个特征合作探究甲、乙两种酒近几年的销售量和价格如下：2002年2006年2010年年度销售量/万瓶150180210该年度的单价/元405060甲品牌酒的产量和价格2002年2006年2010年年度销售量/万瓶160180200乙品牌酒的产量和价格(1)你认为哪一种酒的价格增长较快？为什么？这与上面画出的折线统计图给你的感觉一致吗？为什么图象会给人这样的感觉？有人根据上面的统计表，制作出甲、乙两种酒的价格变化的折线统计图：(2)甲种酒的销售人员将甲种酒的销售信息制作成了如下的条形统计图.请你也在右面的图中作出甲种酒的年度销售量的条形统计图：(3)两幅条形统计图给你的感觉一样吗？在甲种酒销售人员画的条形统计图中，2010年甲种酒的年度销售量看上去是2002年的多少倍？实际上呢？（1）为了较直观地比较某两个统计量的变化速度，绘制折线统计图应注意什么？（2）为了较直观地反映几个统计量之间的比例关系绘制条形统计图时，应注意什么？议一议在绘制条形统计图时，纵坐标上的起始值应从“0”开始，从而避免造成“误导”、引起“错觉”.小结绘制两幅折线统计图，在比较两个统计量的变化趋势时，应注意横（纵）坐标的一致性．当堂练习1．下面信息中，适合用折线统计图的是（）A．六年级各班的学生人数B．淘淘近六年的体重变化情况C．花生中各种营养成分所占百分比D．冬冬家六月份收支情况【答案】B【详解】解：A．六年级各班的学生人数适合用条形图，不符合题意；B．淘淘近六年的体重变化情况适合用折线图，符合题意；C．花生中各种营养成分所占百分比适合用扇形图，不符合题意；D．冬冬家六月份收支情况适合用条形图，不符合题意；故选：B．2．2022年北京冬季奥运会将在2022年2月4日至20日在北京市和张家口市联合举行．要反映我国在最近五届冬季奥运会上获得奖牌总数的变化情况最好应选择（）A．统计表B．条形统计图C．折线统计图D．扇形统计图【答案】C【分析】可根据扇形统计图、折线统计图、条形统计图各自的特点，分析得结论【详解】解：因为折线统计图能直观的反应数量的变化情况，所以要反应我国在最近五届冬季奥运会上获得奖牌总数的变化情况应选择折线统计图．故选：C．3．某校七年级（1）班体育委员对本班60名同学参加球类项目的情况做了统计（每人选一种），绘制成如图所示统计图，已知“羽毛球”所在扇形的圆心角度数为72°，则该班参加乒乓球和羽毛球项目的人数总和为（）A．20人B．25人C．30人D．35人【答案】C【详解】∵“羽毛球”所在扇形的圆心角度数为72°，∴羽毛球所占百分比为：，∵扇形统计图看出乒乓球占30%，∴羽毛球和乒乓球一共占：50%，∴乒乓球和羽毛球项目的人数总和为：60×50%=30（人），故选C.4．图1表示的是某书店今年1~5月的各月营业总额的情况，图2表示的是该书店“党史”类书籍的各月营业额占书店当月营业总额的百分比情况．若该书店1~5月的营业总额一共是182万元，某同学结合统计图分析得到如下结论：①该书店4月份的营业总额为45万元；②5月份“党史”类书籍的营业额为10.5万元；③4月份“党史”类书籍的营业额最高；④5月份“党史”类书籍的营业额最高，则上述结论中正确的是（）A．④B．②③C．①②③D．①②④【答案】D【详解】解：该书店4月份的营业总额是：182-(30+40+25+42)=45（万元），故①正确；5月份“党史”类书籍的营业额是42×25%=10.5(万元)，故②正确；4月份“党史”类书籍的营业额是45×20%=9(万元)，10.5＞9，故③错误；1一3月份的营业总额以及“党史”类书籍的营业额占当月营业额的百分比都低于4、5月份，而4月份“党史”类书籍的营业额又小于5月份“党史”类书籍的营业额，故④正确，故选：D．5．扇形图能清楚地表示出各部分在总体中所占的_______．扇形图通过扇形的大小来反映各个部分占总体的百分比．且扇形的大小是由_______的大小决定的．条形图能得出具体的人数，扇形图能得出各部分的百分比．【答案】百分比圆心角6．小明将本班全体同学假期用于读书的时间制成了频数分布直方图，图中从左到右各小长方形的高的比是2：3：4：1，且第二小组的频数是15，则小明班里的学生人数是__________．【答案】50【分析】根据频数分布直方图的纵轴表示频数，结合图中从左到右各小长方形的高之比和第二小组的频数，即可求得小明班级的学生人数．【详解】解：∵从左到右各小长方形的高之比为2:3:4:1，∴设从左到右各小长方形的高分别为2x、3x、4x、x，∵第二小组的频数是15，∴3x=15，解得：x=5，∴小明班级学生人数是5×（2+3+4+1）=50（人），故答案为：50．7．某校图书管理员清理课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图不完整的扇形统计图，已知乙类书有90本，则丙类书的本数是__________．【详解】解：总数是：90÷30%=300（本），丙类书的本数是：300×（1-25%-30%）=300×45%=135（本），故答案为：135．8．在一次体育水平测试中，甲、乙两校均有100名学生参加，其中：甲校男生成绩的优秀率为70%，女生成绩的优秀率为50%；乙校男生成绩的优秀率为60%，女生成绩的优秀率为40%．对于此次测试，给出下列三个结论：①甲校学生成绩的优秀率大于乙校学生成绩的优秀率；②甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率；③甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系不确定．其中所有正确结论的序号是_____．【答案】②③【分析】根据给出条件，利用统计学知识逐一加以判断．【详解】解：由题意得，甲校学生成绩优秀率在50%与70%之间，乙校学生成绩的优秀率在40%与60%之间，不能确定哪个学校的优秀率大，①错误；②甲乙两校所有男生的优秀率在60%与70%之间，甲乙两校所有女生成绩的优秀率在40%与50%之间，所以甲乙两校所有男生成绩的优秀率大于甲乙两校所有女生成绩的优秀率，②正确；③甲校学生成绩的优秀率与学校的男女生的比例有关，不能由甲乙两校所有学生成绩的优秀率的大小关系确定，③正确；所有正确的结论序号是②③．故答案为：②③．9．为积极落实国家“双减”政策，某学校举办读书节，购买了一批课外读物，为使购买的课外读物满足同学们的需求，学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查（每位同学只选一类），如图是根据调查结果绘制的两幅不完整的统计图．请你根据统计图提供的信息，解答下列问题：(1)本次调查中，一共调查了________名同学？（直接填答案）(2)m=________，n=________．（直接填答案）(3)根据调查的结果，请你给学校购买课外读物提供两条合理化建议．【详解】（1）解：由题意可得，本次调查的学生有：140÷35%=400（名），故答案为：400；（2）n=400×30%=120，m=400-140-120-60=80，故答案为：80，120；（3）建议如下：①学校购买课外读物时，文学类的书多采购一些，科普类的书多采购一些；②艺术类和其他少类采购一些（答案不唯一）．10．2022年3月28日是第27个全国中小学生安全教育日．某校为调查本校学生对安全知识的了解情况，从全校学生中随机抽取若干名学生进行测试，测试后发现所有测试的学生成绩均不低于50分将全部测试成绩x（单位：分）进行整理后分为五组（50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x＜100），并绘制成如下的频数直方图（如图）．请根据所给信息，解答下列问题：(1)在这次调查中，一共抽取了___________名学生；(2)若测试成绩达到80分及以上为优秀，请你估计全校960名学生对安全知识的了解情况为优秀的学生人数；(3)为了进一步做好学生安全教育工作，根据调查结果，请你为学校提一条合理化建议．【答案】(1)40(2)480人(3)加强安全知识教育，普及安全知识；通过多种形式（课外活动、知识竞赛等），提高安全意识；结合校内、校外具体活动（应急演练、参观体验、紧急救援等），提高避险能力【详解】（1）由频数分布直方图可得，一共抽取：4+6+10+12+8=40（人）故答案为：40；（2）960×（人），所以优秀的学生人数约为480人；（3）加强安全知识教育，普及安全知识；通过多种形式（课外活动、知识竞赛等），提高安全意识；结合校内、校外具体活动（应急演练、参观体验、紧急救援等），提高避险能力．课堂小结统计图的选择统计图的选择{统计图引起的错觉条形统计图注意事项{扇形统计图引起的错觉折线统计图注意事项三种统计图的特点{合理选择统计图表示数据{{{