第6章-数据与分析-单元复习(课件)-2022-2023学年八年级数学上册同步精品课堂(北师大版)

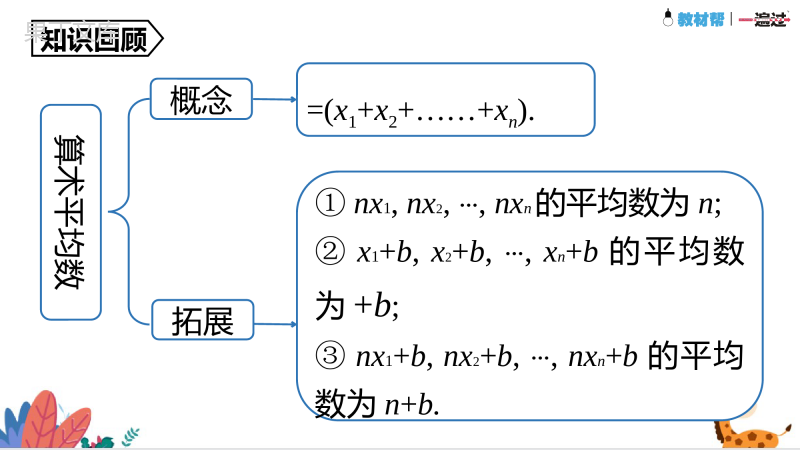
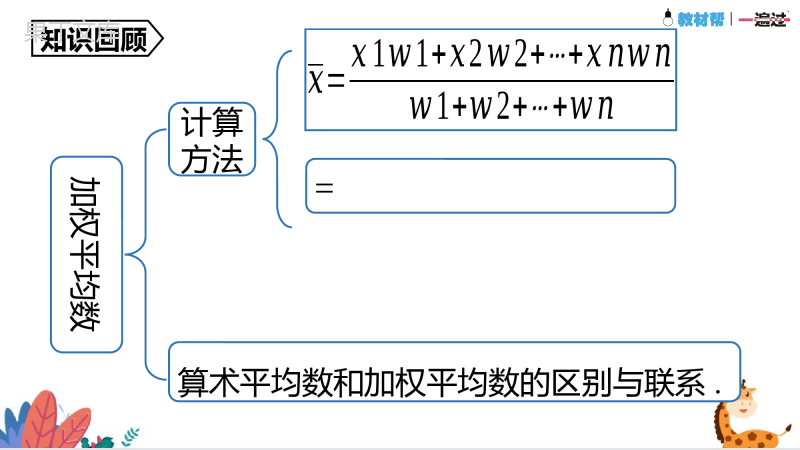
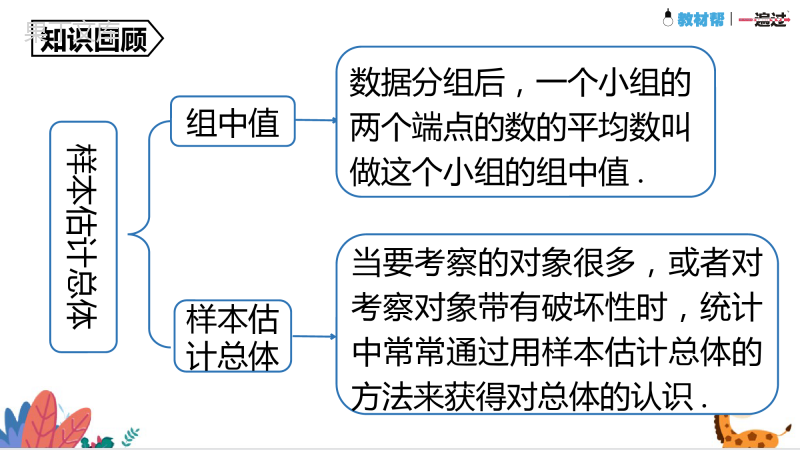
第6章数据与分析单元复习算术平均数概念拓展=(x1+x2+……+xn).①nx1,nx2,,⋯nxn的平均数为n;②x1+b,x2+b,,⋯xn+b的平均数为+b;③nx1+b,nx2+b,,⋯nxn+b的平均数为n+b.知识回顾平均数的性质若一组数据x1，x2，⋯xn的平均数为，则有：（1）数据nx1，nx2，⋯nxn的平均数为n；（2）数据x1+b，x2+b，⋯xn+b的平均数为+b；（3）数据nx1+b，nx2+b，⋯nxn+b的平均数为n+b.知识回顾加权平均数计算方法?=?1?1+?2?2+⋯+?????1+?2+⋯+??算术平均数和加权平均数的区别与联系.=知识回顾样本估计总体组中值样本估计总体数据分组后，一个小组的两个端点的数的平均数叫做这个小组的组中值.当要考察的对象很多，或者对考察对象带有破坏性时，统计中常常通过用样本估计总体的方法来获得对总体的认识.知识回顾中位数概念特点①由小到大排列（或由大到小排列）②中间的数或中间两个数的平均数可能是这组数据中的某个数，也可能不是这组数据中的数.知识回顾众数概念注意一组数据中出现次数最多的数据称为这组数据的众数.众数是一组数据中出现次数最多的数据，而不是数据出现的次数.知识回顾方差概念意义….方差越大，数据的波动越大；方差越小，数据的波动越小.知识回顾作用步骤比较数据的稳定性.先计算样本数据的平均数，然后计算样本方差，再利用样本方差来估计总体数据的波动情况．用样本方差估计总体方差知识回顾1.算术平均数一般地，如果有n个数x1，x2，，⋯xn，那么我们把(x1+x2++⋯xn)叫做这n个数的算术平均数，简称平均数，记作，读作x拔，则有=(x1+x2++⋯xn).2.加权平均数一般地，如果有n个数x1，x2，，⋯xn的权分别为w1，w2，，⋯wn，那么我们把叫做这n个数的加权平均数.在求n个数的平均数时，如果x1出现f1次，x2出现f2次，，⋯xk出现fk次（这里的f1+f2+⋯+fk=n），那么这n个数的平均数=.也叫做x1，x2，，⋯xk这k个数的加权平均数，其中f1，f2，，⋯fk分别叫做x1，x2，，⋯xk的权.4.中位数将一组数据按照由小到大（或由大到小）的顺序排列，如果数据的个数是奇数，则称处于中间位置的数为这组数据的中位数；如果数据的个数是偶数，则称中间两个数据的平均数为这组数据的中位数.5.众数一组数据中出现次数最多的数据称为这组数据的众数.注意：众数是一组数据中出现次数最多的数据，而不是数据出现的次数.6.方差设有n个数据x1，x2，，⋯xn，各数据与它们的平均数的差的平方分别是，，我们用这些值的平均数，即用+来衡量这组数据波动的大小，并把它叫做这组数据的方差，记作.7.方差的意义方差可以反映数据的波动程度，即：方差越大，数据的波动越大；方差越小，数据的波动越小.8.用样本方差估计总体方差用样本估计总体是统计的基本思想，类似于用样本的平均数估计总体的平均数，考察总体方差的时候，如果考察的总体包含很多个体，或者考察本身带有破坏性，实际中常常会用样本的方差来估计总体的方差.1.某公司33名职工的月工资（以元为单位）如下：（1）求该公司职工月工资的平均数、中位数、众数.（精确到个位）职工董事长副董事长董事总经理经理管理员职员人数11215320工资5500500035003000250020001500（3）你认为哪个统计量更能反映这个公司职工的月工资水平？结合问题谈一谈你的看法.（2）假设副董事长的工资从5000元提升到20000元，董事长的工资从5500元提升到30000元，那么新的平均数、中位数、众数又是什么？（精确到个位）解析：（1）平均数（元）把这33个数据按照从小到大的顺序可得中位数为1500.这33个数据中出现次数最多的数据是1500，出现了20次，所以众数为1500.（2）新的平均数（元）把这33个数据按照从小到大的顺序可得新的中位数仍为1500.这33个数据中出现次数最多的数据是1500，出现了20次，所以新的众数仍为1500.（3）中位数或众数都能反映出这个公司职工的月工资水平.由于董事长、副董事长的工资偏高，使月平均工资与绝大多数职工的月工资差距很大，也就是说用平均数来反映这个公司职工的月工资水平有很大误差.选择合适的统计量表示一组数据集中趋势的方法当一组数据中某些数据重复出现时，众数往往作为首选的统计量；当个别数据偏差较大时，常用中位数反映该组数据的集中趋势.选择的统计量要能代表这组数据全部或绝大部分的特征.2.某中学数学活动小组为了调查居民的用水情况，从某社区的1500户家庭中随机抽取了30户家庭的月用水量，结果如下表所示：月用水量/吨34578910户数43511421解：平均数为（吨），众数是7吨，中位数是7吨.（1）求这30户家庭月用水量的平均数、众数和中位数；月用水量/吨34578910户数43511421由题意可知15006.2=9300（吨），所以该社区月用水量约为9300吨.（2）根据上述数据，试估计该社区的月用水量；（3）由于我国水资源缺乏，许多城市常利用分段计费的方法引导市民节约用水，即规定每个家庭的月基本用水量为m（吨），家庭月用水量不超过m（吨）的部分按原价收费，超过m（吨）的部分加倍收费，你认为上述问题中的平均数、众数和中位数哪个作为基本用水量比较合适？（3）以中位数或者众数作为月基本用水量较为合理.理由：因为这样既可以满足大多数家庭用水量，也可以引导用水量高于7吨的家庭节约用水.3.甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全）：某同学计算出了甲的成绩平均数是9，方差是[++]=0.8，请作答：（1）在图中用折线统计图将甲运动员的成绩表示出来；（2）若甲、乙射击成绩平均数都一样，则a+b=.解析：a+b=95-10-9-9=17.17解：a=7，b=10或a=10，b=7.理由如下：∵甲的成绩比乙的成绩稳定，所以乙的方差>0.8.∴[++]>0.8.即(a-9)2+(b-9)2>3.∵a+b=17，且a，b均小于或等于10.（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出a，b的所有可能取值，并说明理由.∴当a=7，b=10时，(a-9)2+(b-9)2>3，符合题意.当a=8，b=9时，(a-9)2+(b-9)2<3，不符合题意.当a=9，b=8时，(a-9)2+(b-9)2<3，不符合题意.当a=10，b=7时，(a-9)2+(b-9)2>3，符合题意.∴a=7，b=10或a=10，b=7.4.某班拟派一名跳远运动员参加学校运动会，对甲、乙两名跳远运动员进行了8次测试，他们的成绩（单位：m）如下：甲：3.68，3.65，3.68，3.69，3.74，3.73，3.68，3.67乙：解：∵8次测试中，甲有2次成绩超过3.70m，而乙有5次成绩超过3.70m，∴应该派乙运动员去参加比赛.易错警示：事实上，要派谁去就要看谁的成绩更容易达到或超过3.70m.本题易错误地通过方差的大小来确定甲应该去，没有结合实际情况进行分析.5.如图是某市连续5天的天气情况.解：（1）5天中日最高气温的平均数为5天中日最低气温的平均数为（1）利用方差判断该城市这5天的日最高气温波动大还是日最低气温波动大？5天中日最高气温的方差5天中日最低气温的方差所以该市5天的日最低气温的波动较大.解：25日、26日、27日的天气现象依次是大雨、中雨、晴，空气质量依次是良、优、优，说明了下雨后空气质量改善了.25日、26日、27日、28日、29日的日温差依次是2℃、3℃、8℃、10℃、7℃，可以看出雨天的日温差较小.（2）根据图中提供的信息，请再写出两个不同类型的结论.