第1课时-平均数(课件)-2022-2023学年八年级数学上册同步精品课堂(北师大版)

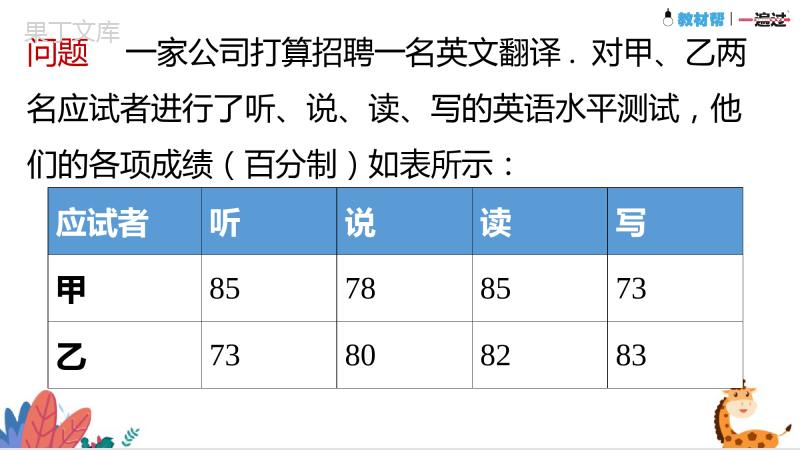
第1课时平均数初中数学8月中旬郑州市一周的最高气温如下表所示.星期一二三四五六日气温/℃38383638363636你能计算出一周的平均最高气温吗？课堂导入问题一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试，他们的各项成绩（百分制）如表所示：应试者听说读写甲85788573乙73808283如果这家公司想招一名综合能力较强的翻译，计算两名应试者的平均成绩（百分制）.从他们的成绩来看，应该录取谁？综合能力需要同时对听、说、读、写进行考量，分别计算出甲、乙四项的平均成绩.甲的平均成绩为：=80.25.乙的平均成绩为：=79.5.从计算结果来看，甲的平均成绩比乙的平均成绩高，所以应该录取甲.知识点01：算术平均数新知探究算术平均数：一般地，如果有n个数x1，x2，，⋯xn，那么我们把(x1+x2++⋯xn)叫做这n个数的算术平均数，简称平均数，记作，读作x拔，则=(x1+x2+⋯+xn).注意：（1）一组给定的数据的算术平均数是唯一的；（2）如果所给的数据带有单位，那么这组数据的算术平均数也要带单位，并且算术平均数所带的单位与数据的单位要一致.(3)算术平均数的大小与所给数据里的每个数据都有关，其中任何一个数据的变动都会引起算术平均数的变动.(4)一般地，要了解一组数据的平均水平，计算这组数据的算术平均数即可.但算术平均数容易受极端值的影响，有时它不能代表一组数据的平均水平.知识点02：加权平均数新知探究加权平均数：一般地，若n个数x1，x2，，⋯xn的权分别是w1，w2，，⋯wn，那么我们把叫做这n个数的加权平均数.=80.4“权”加权平均数思考如果这家公司想招一名口语能力较强的翻译，听、说、读、写成绩按照3:3:2:2的比确定，计算那么甲、乙两人谁被录取？听、说、读、写成绩按照3:3:2:2的比确定，这说明倾向于听、说成绩的“重要程甲的平均成绩为=80.5.乙的平均成绩为=78.9.从计算结果来看，甲的平均成绩比乙的平均成绩高，所以应该录取甲.通过上述问题，你能体会到权的作用吗？所以同样一张应试者的应聘成绩单，由于各个数据所赋予的权数不同，造成的录取结果会截然不同.数据的权能够反映数据的相对重要程度.例1一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计，然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%，计算选手的综合成绩（百分制）.进入决赛的前两名选手的单项成绩如表所示，请确定两人的名次.选手演讲内容演讲能力演讲效果A859595B958595解：选手A的最后得分是=90选手B的最后得分是=91由上可知选手B获得第一名，选手A获得第二名.权是百分数的形式在求n个数的平均数时，如果x1出现f1次，x2出现f2次，，⋯xk出现fk次（这里的f1+f2+⋯+fk=n），那么这n个数的平均数=.也叫做x1，x2，，⋯xk这k个数的加权平均数，其中f1，f2，⋯，fk分别叫做x1，x2，，⋯xk的权.(1)权能够反映某个数据的重要程度，权越大，该数据所占的比重越大；权越小，该数据所占的比重越小.(2)权常见的三种表现形式：①数据出现的次数(个数)的形式；②百分数的形式；③连比的形式.例2某跳水队为了解运动员的年龄情况，作了一次年龄调查，结果如下：13岁8人，14岁16人，15岁24人，16岁2人.求这个跳水队运动员的平均年龄(结果取整数).解：这个跳水队运动员的平均年龄为=≈14（岁）.例1为了解5路公共汽车的运营情况，公交部门统计了某天5路公共汽车每个运行班次的载客量，得到下表.这天5路公共汽车平均每班的载客量是多少（结果取整数）？新知探究知识点03：用样本平均数估计总体平均数载客量/人组中值频数（班次）1≤x<2111321≤x<4131541≤x<61512061≤x<81712281≤x<1019118101≤x<12111115频数指相应组中值的权.思考1表格中的组中值指什么？如何确定呢？思考2频数指什么？例如，小组1≤x<21的组中值是.组中值：数据分组后，一个小组的两个端点的数的平均数.统计中常以其代表各组的实际数据.=≈73(人)频数分布表(图)中的加权平均数的求解思路：①不同数据组中组中值的确定；②权的确定.用样本的平均数估计总体的平均数：当要考察的对象很多，或者对考察对象带有破坏性时，统计中常常通过用样本估计总体的方法来获得对总体的认识.（1）一般来说，用样本估计总体时，样本容量越大，样本对总体的估计也越精确，但相应的工作量也越大.因此在实际工作中，样本容量的确定既要考虑问题本身的需要，又要考虑实现的可能性及成本；（2）抽取的样本要有广泛性和代表性，这样有利于估计总体，解决问题.利用计算器求平均数一般的计算器有统计功能，通常需要先按动有关键，使计算器进入统计状态，然后依次输入数据x1，x2，x3，⋯，xk以及它们的权f1，f2，f3，，⋯fk；最后按动求平均数的功能键，计算器便会求出平均数=的值.例2某灯泡厂为测量一批灯泡的使用寿命，从中随机抽查了50只灯泡，它们的使用寿命如下表所示，这批灯泡的平均使用寿命是多少？使用寿命x/h600≤x<10001000≤x<14001400≤x<18001800≤x<22002200≤x<2600灯泡只数51012176你能确定各小组的“组中值”和“权”吗？分析：抽出的50只灯泡的使用寿命组成了一个样本，我们可以利用样本的平均使用寿命来估计这批灯泡的平均使用寿命.解：由表可以得出每组数据的组中值，则抽出的50只灯泡的平均使用寿命为==1672.从计算结果来看，样本的平均数为1672，则可估计这批灯泡的平均使用寿命大约是1672h.现在你能总结出用样本平均数估计总体平均数的一般步骤吗？1.先求出每个范围内的组中值；2.利用加权平均数的计算公式计算.1.已知一组数据x，y，z，m，n的平均数为7，则另一组数据x+10，y-10，z+10，m-10，n+10的平均数为（）.A.6B.7C.9D.12随堂练习C解析：因为x，y，z，m，n的平均数为7，所以x+y+z+m+n=35.所以x+10，y-10，z+10，m-10，n+10的平均数为===9.2.已知数据x1，x2，x3，x4，x5的平均数为a，则数据5x1，5x2，5x3，5x4，5x5的平均数为（）.A.aB.5aC.D.10a这组数据的系数有何特点？B解析：因为x1，x2，x3，x4，x5的平均数为a，所以x1+x2+x3+x4+x5=5a.所以5x1，5x2，5x3，5x4，5x5的平均数为==5a.3.已知数据x1，x2，x3，x4，x5的平均数为a，则数据5+x1，5+x2，5+x3，5+x4，5+x5的平均数为（）.A.aB.5+aC.5aD.10a每一个数据有何变化呢？B解析：因为x1，x2，x3，x4，x5的平均数为a，所以x1+x2+x3+x4+x5=5a.所以5+x1，5+x2，5+x3，5+x4，5+x5的平均数为==5+a.4.已知数据x1，x2，x3，x4，x5的平均数为a，则数据5+5x1，5+5x2，5+5x3，5+5x4，5+5x5的平均数为（）.A.5aB.5+5aC.5+aD.10a猜想一下这组数据的平均数？B解析：x1，x2，x3，x4，x5的平均数为a，所以x1+x2+x3+x4+x5=5a.所以5+5x1，5+5x2，5+5x3，5+5x4，5+5x5的平均数为==5+a.5.为了检查一批零件的质量，从中随机抽取了10件，测得它们的长度分别为（单位：mm）15.0，15.1，15.4，15.0，15.5，15.2，15.2，15.1，15.5，15.3.根据以上数据，你能估计出这批零件的平均长度吗？解:==15.23.样本的平均数为15.23mm，所以这批零件的平均长度约为15.23mm.还有其他方法吗？另解15.0的频数为2，15.1的频数为2，15.2的频数为2，15.3的频数为1，15.4的频数为1，15.5的频数为2.所以==15.23样本的平均数为15.23mm，所以这批零件的平均长度约为15.23mm.6.为了建设“绿色县城”,A县购进了一批香樟树，五年后这些树干的周长情况如下图所示，请你计算出这批香樟树树干的平均周长.如何确定组中值呢？解：样本树干的平均周长是=63.8cm.则这批香樟树干的平均周长为63.8cm.某校为了预测本校九年级男生的体育测试达标情况，随机抽取了部分男生进行了一次模拟测试（满分为50分，成绩均记为整数分），并按此时成绩a（单位：分）分成四个档次：A类（45