自动控制原理课件-第三章线性系统的时域分析法

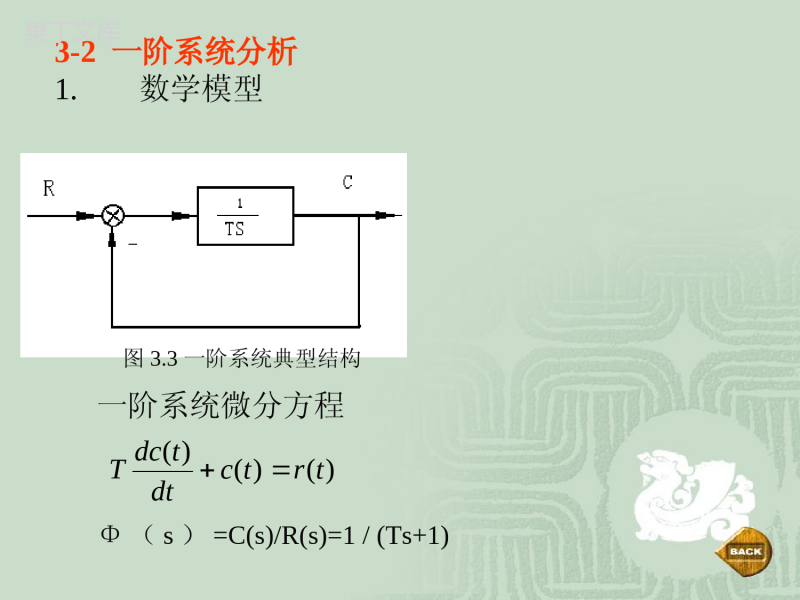
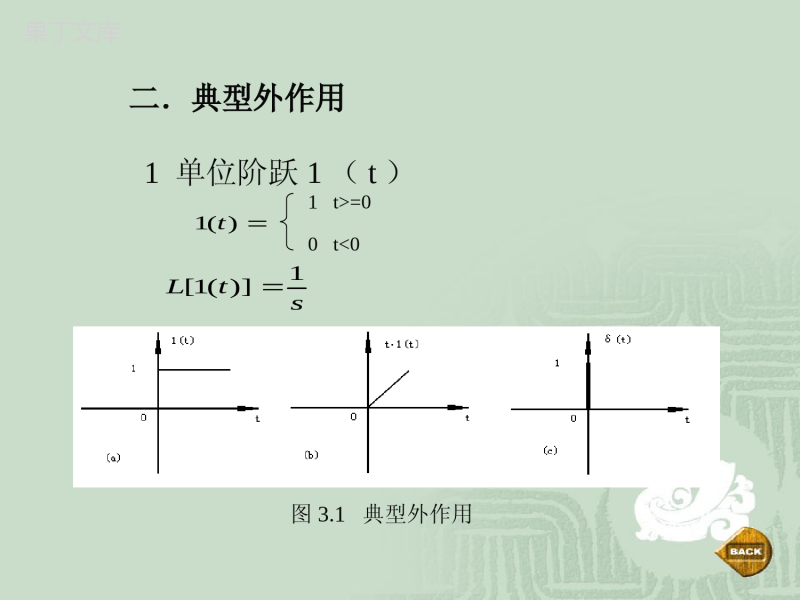
第3章线性系统的时域分析法◆本章主要内容与重点◆典型响应的性能指标◆一阶系统的时域分析◆二阶系统的时域分析◆控制系统的稳定性和代数判据◆稳态误差的分析和计算本章主要内容本章介绍了控制系统时域性能分析法的相关概念和原理。包括各种典型输入信号的特征、控制系统常用性能指标、一阶、二阶系统的暂态响应、脉冲响应函数及其应用、控制系统稳定性及稳定判据、系统稳态误差等。本章重点通过本章学习，应重点掌握典型输入信号的定义与特征、控制系统暂态和稳态性能指标的定义及计算方法、一阶及二阶系统暂态响应的分析方法、控制系统稳定性的基本概念及稳定判据的应用、控制系统的稳态误差概念和误差系数的求取等内容。３.1典型响应和性能指标0)0(0()0()ccc一.典型初状态二．典型外作用1单位阶跃1（t）)(1t图3.1典型外作用stL1)](1[1t>=00t<02.单位斜度t1(t)t1(t)=tt>=00t<00t≠021)](1[sttL3.单位理想脉冲4正弦asinωt001)(dtt且∞t=0δ（t）=L[δ(t)]=1]22]sin[sataL三典型时间响应1.单位阶跃响应Φ（s）R(s)=Φ(s)1/sh(t)=L-1[Φ(s)1/s]2.单位斜坡响应Ct(s)=Φ（s）R(s)=Φ(s)1/s²Ct(t)=L-1[Φ(s)1/s2]3.单位脉冲响应K(s)=Φ（s）R(s)=Φ（s）1=Φ（s）K(t)=L-1[Φ(s)]四．阶跃响应的性能指标图3.2单位阶跃响应曲线及性能指标１、峰值时间tp指输出响应超过稳态值而达到第一个峰值所需时间。２、超调量σ%指暂态过程中输出响应的最大值超过稳态值的百分数。%100)()((%hhPthp３、调节时间ts指当c（t）和c（∞）之间误差达到规定允许值（一般取c（∞）的±５％，有时取±２％）并且以后不再超过此值所需的最小时间。４、稳态误差еss对单位负反馈系统，当时间t趋于无穷大时，系统的单位阶跃响应的实际值（即稳态值）与期望值（即输入量１（t））之差，定义为稳态误差，即еss=1-с(∞)3-2一阶系统分析1.数学模型图3.3一阶系统典型结构Φ（s）=C(s)/R(s)=1/(Ts+1))()()(trtcdttdcT一阶系统微分方程一．单位阶跃响应sTssRssc111)()()(tTeTssLsTsLth1111]111[]111[)(图3.4一阶系统单位阶跃响应曲线TeTdttdhttTt11)(010响应曲线的初始斜率σ%=0ts=3T(对应5%误差带)ts=4T(对应2%误差带)ess=1-h(∞)=1-1=0性能指标三解：1.ts=3T=30.1=0.3秒2.1011.0111.0101.01001/100)()()(sssssRsCs101.0/11001/100)(sKKKsssHHH例3.1一阶系统如图所示，试求系统单位阶跃响应的调节时间ts.如果要求ta=0.1秒，试问系统的反馈系统应调整为何值？T=0.01/KHts=3T=0.03/KH0.1=0.03/KHKH=0.3图3.5系统结构图-例3.2试证一阶响应曲线的次割距相等，且等于T。Attdttdh)(t-t)h(t-1ABAtB-tA=T图3.6一阶系统响应的次割距证：tATABtATeTtte111)1(13-3二阶系统分析1.数学模型)()()(2)(2222trtcdttdcdttcdnnn2222()()()(nnssnssRsC1.单位阶段响应h(t)的一般式sssnsRssCnn12)()()(222C1=ωn2/(s1-s2)s1;C1=ωn2/(s2-s1)s2图３.７二阶系统动态结构则单位阶跃响应一般式tstsnnneCeCsssCssCLsssssLsssnLsCLth212122111212122111]1[]))(([]12([)]([)(-二阶系统的响应特点和特征根的性质ξ>1称过阻尼，由上知，s1，s2为两个不等的负实根。ξ=1称临界阻尼，s1，s2为一对相等的负实根-ωn0<ξ<1称为欠阻尼，特征根将为一对实数部为负的共轭复数。ξ=0称0阻尼，s1，s2由上可看出为一对虚实部的特征根ξ<0则称负阻，系统将出现正实部的特征根。1.过阻尼二阶系统的单位阶跃响应1222,1nnstttsntsnnneeesssesssth)1(22)1(22212212122221115.0115.011)()()()7.145.6(1nst图3.8过阻尼二阶系统h(t)曲线ξ>=0.75%误差带四临界阻尼二阶系统的单位阶跃响应s1,2=-ωnssssscnn1)(1)()(22tnnetscLth)1(1)]([)(1欠阻尼二阶系统的动态性能分析n21nn0jcos在图中称为阻尼角无零点欠阻尼二阶系统的动态性能指标计算公式（1）延迟时间的计算dt)0()1sin(11)(22ttethntn5.0)(dth221)cos1sin(2ln1arcttdndn在绘制出ntd和之间的关系曲线，利用曲线拟合方法，当阻尼比在欠阻尼时ndt22.06.01ndt7.01或（2）上升时间的计算rt21ndrt0)1sin(1)1sin(11)(222rnrntrttethrn（3）峰值时间的计算pt0sin0sin1)(2pdpdtnttttedttdhpnp,2,,0pdt21,ndppdtt（4）超调量的计算%221/221/221)(1)sin()sin(11)1sin(11)(ethetethppntppn%100%21/e根据超调量的定义，并考虑到1)(h%5.1~%4.25%8.0~4.0P.83图3-13给出了欠阻尼二阶系统阻尼比与超调量之间的关系。（5）调节时间的计算为了简化调节时间的计算，一般用包络线来代替实际响应估算调节时间。st在，误差带时，可用以下近似估算公式：8.0%505.0nst5.3也可以用以下公式估算：%511ln31%211ln4122nnst)9.00(%53%24nnst二阶系统单位阶跃响应的性能指标归纳如下：ndt22.06.01ndt7.01或21ndrt21ndpt%100%21/e)9.00(%53%24nnst实际上，上述各项性能指标之间的存在矛盾，例如上升时间（响应速度）和超调量（阻尼程度或相对稳定性）)(1%,20%stppKsrdttt)(sC)(sR)1(ssKs1KsKsKsRsCs)1()()()()1(2KKKn21)2(456.0)1(ln)/1ln(%,100%)3(221/2pppe)/(53.31)4(2sradtpn178.01246.12)5(2KKnn)/(14.31)(097.1cos)6(2sradradarcnd)(374.07.01stnd)(651.012stndr%5)(864.13%2)(485.24sstnns过阻尼二阶系统的动态过程分析过阻尼系统响应缓慢，对于一般要求时间响应快的系统过阻尼响应是不希望的。但在有些应用场合则需要过阻尼响应特性：例如（1）大惯性的温度控制系统、压力控制系统等。（2）指示仪表、记录仪表系统，既要无超调、时间响应尽可能快。另外，有些高阶系统可用过阻尼二阶系统近似。1过阻尼)0(1/1/1)(21/12/21tTTeTTethTtTt动态性能指标：延迟时间、上升时间、调节时间因为求上述指标，要解一个超越方程，只能用数值方法求解。利用曲线逆合法给出近似公式ndt22.06.011（1）延迟时间计算dt21212122/2)/(1,112TTTTTsTsssnn（2）上升时间计算p.86图3-16rtnrt25.111211~TTTts（3）调节时间计算p.86图3-17st12175.41/1TtTTs)(sc)(sr)1(TssK例：角度随动系统如图所示，设K为开环增益，T=0.1(s)为伺服电动机的时间常数。若要求：单位阶跃响应无超调，而且，求K的取值、系统的延迟时间和上升时间)(1sts解：因为考虑系统尽量快的无超调响应，则可选阻尼比为临界阻尼1175.4Tts01)(1/)(222TKsTssDTKsTsTKKsTsKs5.2,2510,10)/(5,1,1012,1.02KKKTKsradTTnnn21221212211,11111TTTTsTTsTsTsn2.051121TT)(95.02.075.475.41sTts)(36.058.12.06.012stnd)(70.055.35.112stnr22222222222)12(2)(/2/2112)(nnnnnnnnnnsssssssssssC二阶系统的单位斜坡响应)0()2sin(112)(2ttettcdtnnn（1）欠阻尼单位斜坡响应dptdttde0)(nssttc2)()2sin(112)()()(2tetctrtedtnnn)2sin(11)(2tetcdtnttnnsssssstcttctrte2)()()()()211(21112sin112)2sin(112)(2222pnpnpnpntntnntnntnnpeeeete%)5(3nstnssttc2)(tnnttnettc2112)(tnnnnettctte21122)()()0(21122)(tetttctnnnn（2）临界阻尼单位斜坡响应%)5(1.4nst（3）过阻尼单位斜坡响应)0(1212121212122)()1(222)1(22222teettctntnnnn)0(1212121212122)()()()1(222)1(22222teetctrtetntnnnnnsse2P.89例3-3)2()5.34(5)(2nnAssssKsG1500,200,5.13,5,5/25.17AAnAKKK（1）改变开环增益就相当于改变了系统阻尼比，单位阶跃响应的超调量和单位斜坡响应稳态误差对阻尼比的要求正好相反，难以折衷；（2）若能选择某个开环增益，满足稳态与动态要求，但难以满足扰动作用下的稳态误差要求；（3）在有些系统不能降低系统的开环增益来换取较小的超调量。二阶系统性能的改善改善二阶系统性能的两种方法：比例-微分控制测速反馈控制（1）比例-微分控制)(sC)(sR)2(2nnss1sTd)(sE)(th1t2t5t4t3t1t2t5t4t3t)(te)(te以角度随动系统为例(a)比例控制[0，t1)系统阻尼小，修正转矩过大；输出超调[t1,t3)转矩反向，起制动作用，但惯性与制动转矩不够大，仍超调[t3,t5)误差又为正，修正转矩又为正，力图使输出趋势减小……(b)控制措施：附加误差的微分量[0，t2)内减小正向修正转矩，增大反向制动转矩；[t2,t4)内减小反向制动转矩，增大正向修正转矩理论分析：比例-微分控制对系统性能的影响2/,)12/()1()(nndKsssTKsG)2()1()(2ndnsssTsGzTzsszsTzszszsTzsTsTsTsTssTsGsGsnddnndndnnnnndnnndndndnndndn212)()2/(2)()2/(2)/1()2/(2)1()(1)()(22222222222222有零点二阶系统zTzsszsTzsGsGsnddnndndn212)()(1)()(2222•比例-微分控制不改变系统的自然频率，但增大了系统的阻尼比。•适当选择开环增益和微分时间常数，既可减小系统斜坡输入时的稳态误差，又可使系统具有满意的阶跃响应性能。1d)/1(arg)]/(1[arg22ddnddntgztgsssszsssssszszsRsGsGsCnndnnndnnndn1211)2(12)()()(1)()(222222222)0()1sin(121)(2222ttezzthdntdnndndP.92给出了：（1）求上升时间的关系曲线；（2）峰值时间；（3）超调量；（4）调节时间结论：（1）微分控制可增大系统阻尼，减小阶跃响应的超调量，缩短调节时间；（2）允许选取较高的开环增益，减小稳态误差；（3）微分对于噪声（高频噪声）有放大作用，在输入端噪声较强时，不用比例-微分控制。]1)2/([12)(2ntnntnKssKsGntKK2（2）测速反馈控制)(sE)(sC)(sR)2(2nnsssKt开环增益2222)(nntnsssnttK21结论：（1）测速反馈可以增加阻尼比，但不影响系统的自然频率；（2）测速反馈不增加系统的零点，对系统性能改善的程度与比例-微分控制是不一样的；（3）测速反馈会降低系统原来的开环增益，通过增益补偿，可不影响原系统的稳态误差。P.94例3-5给出无测速反馈和有测速反馈控制的性能指标P.95给出比例-微分控制与测速反馈控制的各自的优缺点3-4控制系统的稳定性和代数判据一.稳定性的定义如小球平衡位置b点,受外界扰动作用,从b点到点，外力作用去掉后,小球围绕b点作几次反复振荡,最后又回到b点,这时小球的运动是稳定的。abcbb如小球的位置在a或c点,在微小扰动下,一旦偏离平衡位置,则无论怎样,小球再也回不到原来位置,则是不稳定的。定义:若系统在初始偏差作用下,其过渡过程随时间的推移,逐渐衰减并趋于零,具有恢复平衡状态的性能,则称该系统为渐近稳定,简称稳定。反之为不稳定。我们把扰动消失时,系统与平衡位置的偏差看作是系统的初始偏差。线性系统的稳定性只取决于系统本身的结构参数,而与外作用及初始条件无关,是系统的固有特性。二.稳定的充要条件设系统的闭环传递函数为:)()()()()()()()()()()(1110111011101110sRsDsMsCasasasasDbsbsbsbsMsDsMasasasabsbsbsbsRsCsnnnnmmmmnnnnmmmm则输出由于系统的初始条件为零,当输入一个理想的单位脉冲δ(t)时,则系统的输出便是单位脉冲过渡函数k(t),如果,则系统稳定。若是线性系统特征方程的根,且互不相等,则上式可分解为0)(limtkt)()()(,1)]([sDsMsCtL),,2,1(nissi0)(sDniiissCsDsMsC1)()()(式中则通过拉式变换,求出系统的单位脉冲过渡函数为欲满足,则必须各个分量都趋于零。式中为常数,即只有当系统的全部特征根都具有负实部才满足。issiisssDsMC)()()(nitsiieCtctk1)()(0)(limtktiCis稳定的充要条件是:系统特征方程的全部根都具有负实部,或者闭环传递函数的全部极点均在s平面的虚轴之左。特征方程有重根时,上述充要条件完全适用。i0itk(t)ci000cicitt稳定临界稳定发散实根情况下系统的稳定性0tk(t)000tt衰减振荡－稳定等幅振荡－临界稳定发散振荡－不稳定共轭复根情况下系统的稳定性jjj三.劳思稳定判据不必求解特征方程的根,而是直接根据特征方程的系数,判断系统的稳定性,回避求解高次方程的困难。1.系统稳定的必要条件:特征方程中所有项的系数均大于0.只要有一项等于或小于0,则为不稳定系统。充分条件:Routh表第一列元素均大于0。2.Routh表的列写方法特征方程为则Routh表为(在下页中)00122334455asasasasasa0011012110112421224051414253434355000241asdcabbcsacbbaabsbaaaaabaaaaasaaasaaas则系统稳定的充要条件:劳思表中第一列元素全部大于0。若出现小于0的元素,则系统不稳定。且第一列元素符号改变的次数等于系统正实部根的个数。例:50651425310543201234234sssssssss则系统不稳定,且有两个正实部根。（即有2个根在S的右半平面。一次方程:a1,a0同号则系统稳定。二次方程:a1,a2,a0同号则系统稳定。三次方程:a0,a1,a2,a3均大于0,且a1a2>a3a0,则系统稳定。001asa00122asasa0012233asasasa3劳思判据应用（1）劳思表不但可判断系统的稳定性，而且可以选择使系统稳定的调节器参数的数值(分析参数对稳定性的影响)。（2）利用劳思表能判断特征根的位置分布情况。例1试分析系统结构参数对稳定性的影响,系统的闭环传递函数为式中，Kk为系统的开环放大系数。123111KBKKWsTsTsTsK解：系统特征方程为3212312132312310KTTTsTTTTTTsTTTsK列劳斯表，整理得假设T1=T2=T3，则使系统稳定的临界放大系数Kk为=8。如果取T2=T3，T1=10T2，则使系统稳定的临界放大系数变为Kk=24.2。由此可见，将各时间常数的数值错开，可以允许较大的开环放大系数。33122123112302KTTTTTTKTTTTTT例2:结构图如图所示,试分析τ取何值能保证系统稳定.SS1)1(10SS)(sR)(sC解:求系统特征方程0)1(1011)(1SSSSSWb0101023SSS建立劳思表:根据劳思判据,要保证系统稳定,劳思表第一列的系数应大于0.1例3:系统结构如下图所示,求能保证系统稳定的局部反馈系数kf的数值。)(sRS11)1(10SSSKf)(sC系统结构图方法1:)(sRS11)101(10fKSSC(S))(sR)101()1(102fKSSSC(S)特征方程:0)1(10)101(2SKSSf即:01010)101(23SSKSf根据劳思判据……kf>0另一种方法:)(sRS11)1(10SS12SKSf)(sC)(sR210S112SKSf)(sC)(sR1010)101()1(1023SSKSSf)(sC系统特征方程:01010)101(23SSKSf根据劳思判据……kf>0例4确定系统稳定的K、T值。解:系统的特征方程为列出劳斯表要使系统稳定，第一列元素的符号均应大于零。由此得则稳定条件为：,0