第一章自动控制的一般概念1-1自动控制的任务1-2自动控制的基本方式1-3对控制系统的性能要求返回主目录1-1自动控制的任务通常,在自动控制技术中,把工作的机器设备称为被控对象,把表征这些机器设备工作状态的物理参量称为被控量,而对这些物理参量的要求值称为给定值或希望值(或参考输入)。则控制的任务可概括为:使被控对象的被控量等于给定值。返回子目录下面通过具体例子来说明自动控制和自动控制系统的概念控制器气动阀门流入Q1浮子水箱流出Q2H水位自动控制系统控制器气动阀门流入Q1浮子水箱流出Q2H水位自动控制系统•控制任务:维持水箱内水位恒定;•控制装置:气动阀门、控制器;•受控对象:水箱、供水系统;•被控量:水箱内水位的高度;控制器气动阀门流入Q1浮子水箱流出Q2H水位自动控制系统•给定值:控制器刻度盘指针标定的预定水位高度;•测量装置:浮子;•比较装置:控制器刻度盘;•干扰:水的流出量和流入量的变化都将破坏水位保持恒定;自动控制即没有人直接参与的控制,其基本任务是:在无人直接参与的情况下,只利用控制装置操纵被控对象,使被控制量等于给定值。自动控制系统:指能够完成自动控制任务的设备,一般由控制装置和被控对象组成。由此可见:1-2自动控制的基本方式被控量比较执行测量被控对象实测值干扰测量给定值H自动控制方框图返回子目录'H在上图中,除被控对象外的其余部分统称为控制装置,它必须具备以下三种职能部件。测量元件:用以测量被控量或干扰量。比较元件:将被控量与给定值进行比较。执行元件:根据比较后的偏差,产生执行作用,去操纵被控对象参与控制的信号来自三条通道,即给定值、干扰量、被控量。•开环控制–按给定值操纵的开环控制–按干扰补偿的开环控制•按偏差调节的闭环控制•复合控制下面根据不同的信号源来分析自动控制的几种基本控制方式一、按给定值操纵的开环控制计算执行受控对象给定值干扰被控量按给定值操纵的开环控制系统原理方框图•开环控制——系统的输出端与输入端之间不存在反馈回路,输出量对系统的控制作用没有影响。炉温控制系统炉温控制系统原理方框图定时开关炉子电阻丝0T给定炉温T实际炉温按给定值操纵的开环控制特点:控制装置只按给定值来控制受控对象优点:控制系统结构简单,相对来说成本低。缺点:对可能出现的被控量偏离给定值的偏差没有任何修正能力,抗干扰能力差,控制精度不高。二、按干扰补偿的开环控制定义:利用干扰信号产生控制作用,以及时补偿干扰对被控量的直接影响。计算测量受控对象执行干扰被控量特点:只能对可测干扰进行补偿,对不可测干扰以及受控对象、各功能部件内部参数变化对被控量的影响,系统自身无法控制。适用于:存在强干扰且变化比较剧烈的场合。水位高度控制系统原理图水位高度控制系统原理方框图三、按偏差调节的闭环控制特点:通过计算被控量和给定值的差值来控制被控对象。优点:可以自动调节由于干扰和内部参数的变化而引起的变动。计算比较给定值E执行被控对象干扰被控量测量-按偏差调节的系统原理方框图如上图所示,反馈回来的信号与给定值相减,即根据偏差进行控制,称为负反馈,反之称为正反馈。这种控制方式控制精度较高,因为无论是干扰的作用,还是系统结构参数的变化,只要被控量偏离给定值,系统就会自行纠偏。但是闭环控制系统的参数如果匹配得不好,会造成被控量的较大摆动,甚至系统无法正常工作。飞机自动驾驶系统原理图控制任务:系统在任何扰动作用下,保持飞机俯仰角不变。被控对象:飞机。被控量:飞机的俯仰角。俯仰角控制系统原理方框图四、复合控制复合控制就是开环控制和闭环控制相结合的一种控制。实质上,它是在闭环控制回路的基础上,附加了一个输入信号或扰动作用的顺馈通路,来提高系统的控制精度。控制装置被控对象CR—补偿装置a.按输入作用补偿b.按扰动作用补偿n控制装置被控对象CR—补偿装置1-3对控制系统的性能要求定义:通常将系统受到给定值或干扰信号作用后,控制被控量变化的全过程称为系统的动态过程。工程上常从稳、快、准三个方面来评价控制系统。稳:指动态过程的平稳性。快:指动态过程的快速性。准:指动态过程的最终精度。返回子目录稳:指动态过程的平稳性控制系统动态过程曲线如上图所示,系统在外力作用下,输出逐渐与期望值一致,则系统是稳定的,如曲线①所示;反之,输出如曲线②所示,则系统是不稳定的。快:指动态过程的快速性快速性即动态过程进行的时间的长短。过程时间越短,说明系统快速性越好,反之说明系统响应迟钝,如曲线①所示。稳和快反映了系统动态过程性能的好坏。既快又稳,表明系统的动态精度高。准:指系统在动态过程结束后,其被控量(或反馈量)与给定值的偏差,这一偏差称为稳态误差,是衡量稳态精度的指标,反映了系统后期稳态的性能。以上分析的稳、快、准三方面的性能指标往往由于被控对象的具体情况不同,各系统要求也有所侧重,而且同一个系统的稳、快、准的要求是相互制约的。第二章自动控制系统的数学模型2-1控制系统微分方程的建立2-2非线性微分方程的线性化2-3传递函数(transferfunction)2-4动态结构图2-5系统的脉冲响应函数2-6典型反馈系统传递函数返回主目录基本要求基本要求1.了解建立系统动态微分方程的一般方法。2.熟悉拉氏变换的基本法则及典型函数的拉氏变换形式。3.掌握用拉氏变换求解微分方程的方法。4.掌握传递函数的概念及性质。5.掌握典型环节的传递函数形式。返回子目录6.掌握由系统微分方程组建立动态结构图的方法。7.掌握用动态结构图等效变换求传递函数和用梅森公式求传递函数的方法。8.掌握系统的开环传递函数、闭环传递函数,对参考输入和对干扰的系统闭环传递函数及误差传递函数的概念。分析和设计任何一个控制系统,首要任务是建立系统的数学模型。系统的数学模型是描述系统输入、输出变量以及内部各变量之间关系的数学表达式。建立数学模型的方法分为解析法和实验法解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表达式,并实验验证。实验法:对系统或元件输入一定形式的信号(阶跃信号、单位脉冲信号、正弦信号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。总结:解析方法适用于简单、典型、常见的系统,而实验方法适用于复杂、非常见的系统。实际上常常是把这两种方法结合起来建立数学模型更为有效。2-1控制系统微分方程的建立基本步骤:分析各元件的工作原理,明确输入、输出量建立输入、输出量的动态联系消去中间变量标准化微分方程返回子目录列写微分方程的一般方法例1.列写如图所示RC网络的微分方程。RCuruci解:由基尔霍夫定律得:式中:i为流经电阻R和电容C的电流,消去中间变量i,可得:TRC令(时间常数),则微分方程为:idtiRuCr1idtuCc1(21)(23)ccrduTuudt(22)ccrduRCuudt•例2.设有一弹簧质量阻尼动力系统如图所示,当外力F(t)作用于系统时,系统将产生运动,试写出外力F(t)与质量块的位移y(t)之间的动态方程。其中弹簧的弹性系数为k,阻尼器的阻尼系数为f,质量块的质量为m。MF(t)kfy(t)0iF解:分析质量块m受力,有外力F,弹簧恢复力Ky(t)阻尼力惯性力由于m受力平衡,所以()/fdytdt22/mdydt式中:Fi是作用于质量块上的主动力,约束力以及惯性力。将各力代入上等式,则得MF(t)kfy(t)22()()()()dytdytmfKytFtdtdt(24)式中:y——m的位移(m);f——阻尼系数(N·s/m);K——弹簧刚度(N/m)。将式(2-4)的微分方程标准化22()()1()()mdytfdytytFtKdtKdtK222()()2()()dytdytTTytkFtdtdt(25)T称为时间常数,为阻尼比。显然,上式描述了m-K-f系统的动态关系,它是一个二阶线性定常微分方程。令,即/TmK2/TfK/2fmK,则式可写成(24)1/kK2-2非线性微分方程的线性化在实际工程中,构成系统的元件都具有不同程度的非线性,如下图所示。返回子目录于是,建立的动态方程就是非线性微分方程,对其求解有诸多困难,因此,对非线性问题做线性化处理确有必要。对弱非线性的线性化如上图(a),当输入信号很小时,忽略非线性影响,近似为放大特性。对(b)和(c),当死区或间隙很小时(相对于输入信号)同样忽略其影响,也近似为放大特性,如图中虚线所示。平衡位置附近的小偏差线性化输入和输出关系具有如下图所示的非线性特性。在平衡点A(x0,y0)处,当系统受到干扰,y只在A附近变化,则可对A处的输出—输入关系函数按泰勒级数展开,由数学关系可知,当很小时,可用A处的切线方程代替曲线方程(非线性),即小偏差线性化。x可得,简记为y=kx。若非线性函数由两个自变量,如z=f(x,y),则在平衡点处可展成(忽略高次项)0xdfyxkxdx0000(,)(,)xyxyvffzxyxy经过上述线性化后,就把非线性关系变成了线性关系,从而使问题大大简化。但对于如图(d)所示为强非线性,只能采用第七章的非线性理论来分析。对于线性系统,可采用叠加原理来分析系统。叠加原理叠加原理含有两重含义,即可叠加性和均匀性(或叫齐次性)。例:设线性微分方程式为2()()()()dctdctctrtdtdt若时,方程有解,而时,方程有解,分别代入上式且将两式相加,则显然有,当+时,必存在解为,即为可叠加性。1()()rtrt1()ct2()()rtrt2()ct1()()rtrt2()rt12()()()ctctct上述结果表明,两个外作用同时加于系统产生的响应等于各个外作用单独作用于系统产生的响应之和,而且外作用增强若干倍,系统响应也增强若干倍,这就是叠加原理。若时,为实数,则方程解为,这就是齐次性。1()()rtart1()()ctacta2-3传递函数(transferfunction)传递函数的概念与定义线性定常系统在输入、输出初始条件均为零的条件下,输出的拉氏变换与输入的拉氏变换之比,称为该系统的传递函数。返回子目录这里,“初始条件为零”有两方面含义:0一指输入作用是t=0后才加于系统的,因此输入量及其各阶导数,在t=时的值为零。0二指输入信号作用于系统之前系统是静止的,即t=时,系统的输出量及各阶导数为零。许多情况下传递函数是能完全反映系统的动态性能的。一、传递函数的概念与定义G(s)Ur(s)Uc(s))s(U)s(U)s(Grc传递函数是关于复变量s的有理真分式,它的分子,分母的阶次是:。nm二、关于传递函数的几点说明传递函数仅适用于线性定常系统,否则无法用拉氏变换导出;传递函数完全取决于系统内部的结构、参数,而与输入、输出无关;传递函数只表明一个特定的输入、输出关系,对于多输入、多输出系统来说没有统一的传递函数;(可定义传递函数矩阵,见第九章)传递函数的拉氏反变换为该系统的脉冲响应函数,因为()()()GsCsRs/当时,,所以,()()rtt()1Rs111()()()()()ctLCsLGsRsLGs一定的传递函数有一定的零、极点分布图与之对应。这将在第四章根轨迹中详述。传递函数是在零初始条件下建立的,因此,它只是系统的零状态模型,有一定的局限性,但它有现实意义,而且容易实现。三、传递函数举例说明例1.如图所示的RLC无源网络,图中电感为L(亨利),电阻为R(欧姆),电容为C(法),试求输入电压ui(t)与输出电压uo(t)之间的传递函数。uiRCucLi解:为了改善系统的性能,常引入图示的无源网络作为校正元件。无源网络通常由电阻、电容、电感组成,利用电路理论可方便地求出其动态方程,对其进行拉氏变换即可求出传递函数。这里用直接求的方法。因为电阻、电容、电感的复阻抗分别为R、1∕Cs、Ls,它们的串并联运算关系类同电阻。则传递函数为2()1/1()1/1oiUssCUsLsRsCLCsRCs()1/()iUsLsRsCIs()1/()oUssCIs四、典型环节一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见的几种形式有:①比例环节,传递函数为:()GsK②积分环节,传递函数为1()Gss③微分环节,传递函数为()Gss④惯性环节,传递函数为1()1GsTs⑤一阶微分环节,传递函数为()1Gss式中:,T为时间常数。⑥二阶振荡环节,传递函数为221()21GsTsTs式中:T为时间常数,为阻尼系数。⑦二阶微分环节,传递函数为22()21Gsss式中:为时间常数,为阻尼系数此外,还经常遇到一种延迟环节,设延迟时间为,该环节的传递函数为:()sGse2-4动态结构图动态结构图是一种数学模型,采用它将更便于求传递函数,同时能形象直观地表明输入信号在系统或元件中的传递过程。返回子目录一、动态结构图的概念系统的动态结构图由若干基本符号构成。构成动态结构图的基本符号有四种,即信号线、传递方框、综合点和引出点。1.信号线表示信号输入、输出的通道。箭头代表信号传递的方向。2.传递方框G(s)方框的两侧为输入信号线和输出信号线,方框内写入该输入、输出之间的传递函数G(s)。3.综合点综合点亦称加减点,表示几个信号相加、减,叉圈符号的输出量即为诸信号的代数和,负信号需在信号线的箭头附近标以负号。+省略时也表示+4.引出点表示同一信号传输到几个地方。()Us()Us二、动态结构图的基本连接形式1.串联连接G1(s)G2(s)X(s)Y(s)方框与方框通过信号线相连,前一个方框的输出作为后一个方框的输入,这种形式的连接称为串联连接。2.并联连接G1(s)G2(s)X(s)-+Y(s)两个或两个以上的方框,具有同一个输入信号,并以各方框输出信号的代数和作为输出信号,这种形式的连接称为并联连接。3.反馈连接一个方框的输出信号输入到另一个方框后,得到的输出再返回到这个方框的输入端,构成输入信号的一部分。这种连接形式称为反馈连接。G(s)R(s)-C(s)H(s)三、系统动态结构图的构成构成原则:按照动态结构图的基本连接形式,构成系统的各个环节,连接成系统的动态结构图。以机电随动系统为例,如下图所示举例说明系统动态结构图的构成其象方程组如下:()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss系统各元部件的动态结构图(1))(sr)(sc)(se()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss)(sr)(sc)(se系统各元部件的动态结构图(2))(sr)(sc)(sesK)(sUs()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss)(sesK)(sUs系统各元部件的动态结构图(3)aK)(sUs)(sUa)(sr)(sc)(sesK)(sUsaK)(sUa()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss系统各元部件的动态结构图(4)()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs)(sr)(sc)(sesK)(sUsaK)(sUa1aaLsR()bsE()asI()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss系统各元部件的动态结构图(5)()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs)(sIamC)(sMmmC)(sMm)(sr)(sc)(sesK)(sUsaK)(sUa1aaLsR()bsE()asI()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss系统各元部件的动态结构图(6))(sr)(sc)(sesK)(sUsaK)(sUa1aaLsR()bsE()asI)(smsfJs21mC)(sMm()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs)(sMm)(smsfJs21sfJs1()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss系统各元部件的动态结构图(7)()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs)(smsKb)(sEb)(sr)(sc)(sesK)(sUsaK)(sUa1aaLsR()bsE()asI)(smsfJs21mC)(sMmbsK系统各元部件的动态结构图(8)()()()()aaaaabUsRIsLsIsEs()()()ercsss()()sseUsKs()()aasUsKUs()()mmaMsCIs2()()mmmJssMfss1()()cmssi()()bbmEsKss)(smi1)(sci1)(sc)(sr)(sc)(sesK)(sUsaK)(sUa1aaLsR()bsE()asI)(smsfJs21mC)(sMmbsK四结构图的等效变换思路:在保证总体动态关系不变的条件下,设法将原结构逐步地进行归并和简化,最终变换为输入量对输出量的一个方框。1.串联结构的等效变换(1)串联结构图G1(s)G2(s)R(s)C(s)U(s)等效变换证明推导)()()(1sRsGsUG1(s)G2(s)R(s)C(s)U(s))()()(2sUsGsC1.串联结构的等效变换(2)等效变换证明推导)()()()()()()()(2121sGsGsRsCsRsGsGsCG1(s)G2(s)R(s)C(s)U(s)1.串联结构的等效变换(3)串联结构的等效变换图G1(s)G2(s)R(s)C(s)U(s)G1(s)•G2(s)R(s)C(s)两个串联的方框可以合并为一个方框,合并后方框的传递函数等于两个方框传递函数的乘积。1.串联结构的等效变换(4)2.并联结构的等效变换并联结构图C1(s)G1(s)G2(s)R(s)C(s)C2(s)等效变换证明推导(1)G1(s)G2(s)R(s)C(s)C1(s)C2(s))()()(11sRsGsC)()()(22sRsGsC2.并联结构的等效变换等效变换证明推导C1(s)G1(s)G2(s)R(s)C(s)C2(s))()()()()()]()([)(2121sGsGsRsCsRsGsGsC并联结构的等效变换图G1(s)G2(s)R(s)C(s)C1(s)C2(s)G1(s)G2(s)R(s)C(s)两个并联的方框可以合并为一个方框,合并后方框的传递函数等于两个方框传递函数的代数和。3.反馈结构的等效变换反馈结构图G(s)R(s)C(s)H(s)B(s)E(s)C(s)=?3.反馈结构的等效变换等效变换证明推导)()()(1)()()(),()()()()()()()()()(sRsHsGsGsCsBsEsBsRsEsHsCsBsEsGsC得消去中间变量G(s)R(s)C(s)H(s)B(s)E(s)3.反馈结构的等效变换反馈结构的等效变换图G(s)R(s)C(s)H(s)B(s)E(s)R(s)C(s))()(1)(sGsHsG4.综合点的移动(后移)综合点后移G(s)R(s)C(s)Q(s)Q(s)?G(s)R(s)C(s)G(s)R(s)C(s)Q(s))()]()([)(sGsQsRsC综合点后移证明推导(移动前)G(s)R(s)C(s)Q(s)??)()()()(sQsGsRsC综合点后移证明推导(移动后)?)()()()(sQsGsRsC移动前)()()()()(sGsQsGsRsCG(s)R(s)C(s)Q(s)Q(s)G(s)R(s)C(s)?移动后综合点后移证明推导(移动前后)G(s)R(s)C(s)Q(s)?)(?sG?)()()()(sQsGsRsC)()()()(sGsQsGsR综合点后移证明推导(移动后)G(s)R(s)C(s)Q(s)G(s)R(s)C(s)Q(s)G(s)综合点后移等效关系图G(s)R(s)C(s)Q(s)Q(s)?G(s)R(s)C(s)综合点前移G(s)R(s)C(s)Q(s))()()()(sQsGsRsC综合点前移证明推导(移动前)G(s)R(s)C(s)Q(s)??)()()()()(sGsQsGsRsC综合点前移证明推导(移动后)?)()()()(sQsGsRsC移动前)()()()(sQsGsRsCG(s)R(s)C(s)Q(s)G(s)R(s)C(s)Q(s)?移动后综合点前移证明推导(移动前后)4.综合点的移动(前移)综合点前移证明推导(移动后))(1?sG?)()()()()(sGsQsGsRsC)()()(sQsGsRG(s)R(s)C(s)Q(s)?4.综合点的移动(前移)综合点前移等效关系图G(s)R(s)C(s)Q(s)G(s)R(s)C(s)Q(s)1/G(s)综合点之间的移动R(s)C(s)Y(s)X(s)R(s)C(s)Y(s)X(s)4.综合点之间的移动结论:结论:多个相邻的综合点可以随意交换位置。R(s)C(s)Y(s)X(s)R(s)C(s)Y(s)X(s)5.引出点的移动引出点后移G(s)R(s)C(s)R(s)?G(s)R(s)C(s)R(s)问题:要保持原来的信号传递关系不变,?等于什么。引出点后移等效变换图G(s)R(s)C(s)R(s)G(s)R(s)C(s)1/G(s)R(s)引出点前移问题:要保持原来的信号传递关系不变,?等于什么。G(s)R(s)C(s)C(s)G(s)R(s)C(s)?C(s)引出点前移等效变换图G(s)R(s)C(s)C(s)G(s)R(s)C(s)G(s)C(s)引出点之间的移动ABR(s)BAR(s)引出点之间的移动相邻引出点交换位置,不改变信号的性质。ABR(s)BAR(s)五举例说明(例1)例1:利用结构图变换法,求位置随动系统的传递函数Qc(s)/Qr(s)。KsKaCmKbs-ML--rcfsJs21aR1i1例题分析由动态结构图可以看出该系统有两个输入r,ML(干扰)。我们知道:传递函数只表示一个特定的输出、输入关系,因此,在求c对r的关系时,根据线性叠加原理,可取力矩ML=0,即认为ML不存在。要点:结构变换的规律是:由内向外逐步进行。例题化简步骤(1)合并串联环节:saKK)(2fsJsRCami1sKbr--c例题化简步骤(2)内反馈环节等效变换:iKKsa)(mbaamCKfRJsRsC-rcsaKK)(2fsJsRCami1sKbr--c例题化简步骤(3)合并串联环节:iCKRfRJssKKCmbaasam][-rciKKsa)(mbaamCKfRJsRsC-rc例题化简步骤(4)反馈环节等效变换:iRCKKsRKCfJsiRCKKamasabmamas)(2rciCKRfRJssKKCmbaasam][-rc例题化简步骤(5)求传递函数Qc(s)/Qr(s):iRCKKsRKCfJsiRCKKsssamasabmamasrc)()()()(2五举例说明(例2)例2:系统动态结构图如下图所示,试求系统传递函数C(s)/R(s)。)(1sG)(2sG)(3sG)(4sG)(1sH)(3sH)(2sH)(sR)(sC---例2(例题分析)本题特点:具有引出点、综合交叉点的多回路结构。例2(解题思路)解题思路:消除交叉连接,由内向外逐步化简。例2(解题方法一之步骤1)将综合点2后移,然后与综合点3交换。)(1sG)(2sG)(3sG)(4sG)(1sH)(3sH)(2sH)(sR)(sC---123ABC例2(解题方法一之步骤2))(1sG)(3sH)(2sG)(3sG)(4sG)(1sH?R(s)C(s)123---例2(解题方法一之步骤3))(1sG)(3sH)(2sG)(3sG)(4sG)(1sH)()(22sHsGR(s)C(s)123---例2(解题方法一之步骤4)内反馈环节等效变换)(1sG)(3sH)(2sG)(3sG)(4sG)(1sH)()(22sHsGR(s)C(s)123---例2(解题方法一之步骤5)内反馈环节等效变换结果)(1sG)(3sH)(2sG)(4sG)(1sH)()()(1)(2323sHsGsGsGR(s)C(s)13--例2(解题方法一之步骤6)串联环节等效变换)(1sG)(3sH)(2sG)(4sG)(1sH)()()(1)(2323sHsGsGsGR(s)C(s)13--例2(解题方法一之步骤7)串联环节等效变换结果)(3sH)(1sH)()()(1)()(23243sHsGsGsGsGR(s)C(s)13)()(21sGsG--例2(解题方法一之步骤8)内反馈环节等效变换)(3sH)(1sH)()()(1)()(23243sHsGsGsGsGR(s)C(s)13)()(21sGsG--例2(解题方法一之步骤9)内反馈环节等效变换结果)(1sH)()()()()()(1)()(34323243sHsGsGsHsGsGsGsGR(s)C(s)1)()(21sGsG-例2(解题方法一之步骤10)反馈环节等效变换)(1sH)()()()()()(1)()(34323243sHsGsGsHsGsGsGsGR(s)C(s)1)()(21sGsG-例2(解题方法一之步骤11)等效变换化简结果143213432324343)()()(1HGGGGHGGsHsGsGGGGGR(s)C(s)例2(解题方法二)将综合点③前移,然后与综合点②交换。)(1sG)(2sG)(3sG)(4sG)(1sH)(3sH)(2sH)(sR)(sC---123ABC例2(解题方法三)引出点A后移)(1sG)(2sG)(3sG)(4sG)(1sH)(3sH)(2sH)(sR)(sC---123ABC例2(解题方法四)引出点B前移)(1sG)(2sG)(3sG)(4sG)(1sH)(3sH)(2sH)(sR)(sC---123ABC结构图化简步骤小结确定输入量与输出量。如果作用在系统上的输入量有多个,则必须分别对每个输入量逐个进行结构图化简,求得各自的传递函数。若结构图中有交叉联系,应运用移动规则,首先将交叉消除,化为无交叉的多回路结构。对多回路结构,可由里向外进行变换,直至变换为一个等效的方框,即得到所求的传递函数。结构图化简注意事项:有效输入信号所对应的综合点尽量不要移动;尽量避免综合点和引出点之间的移动。五、用梅森(S.J.Mason)公式求传递函数梅森公式的一般式为:nKKKPsG1)(梅森公式参数解释:待求的总传递函数;:)(sGkjijiiLLLLLL1且称为特征式,数;条前向通路的总传递函从输入端到输出端第kPk:称余子式;除去后所余下的部分,路所在项条前向通路相接触的回中,将与第在kk:;递函数”之和所有各回路的“回路传:iL积之和;其“回路传递函数”乘两两互不接触的回路,:jiLL”乘积之和;路,其“回路传递函数所有三个互不接触的回:kjiLLL前向通道数;:n注意事项:“回路传递函数”是指反馈回路的前向通路和反馈回路的传递函数的乘积,并且包含代表反馈极性的正、负号。举例说明(梅森公式)例1:试求如图所示系统的传递函数C(s)/R(s)G1H1H2H3G6H4G5G4G3G2R(s)C(s)----求解步骤之一(例1)找出前向通路数nG1H1H2H3G6H4G5G4G3G2R(s)C(s)----求解步骤之一(例1)前向通路数:n=1G1H1H2H3G6H4G5G4G3G2R(s)C(s)----6543211GGGGGGP求解步骤之二(例1)确定系统中的反馈回路数G1H1H2H3G6H4G5G4G3G2R(s)C(s)----1.寻找反馈回路之一G1H1H2H3G6H4G5G4G3G2R(s)C(s)----反馈回路1:L1=-G1G2G3G4G5G6H111.寻找反馈回路之二G1H1H2H3G6H4G5G4G3G2R(s)C(s)----反馈回路2:L2=-G2G3H2211.寻找反馈回路之三G1H1H2H3G6H4G5G4G3G2R(s)C(s)----反馈回路3:L3=-G4G5H31231.寻找反馈回路之四G1H1H2H3G6H4G5G4G3G2R(s)C(s)----反馈回路4:L4=-G3G4H41234利用梅森公式求传递函数(1)411.1ikjijiiLLLLLL求414321iiLLLLL4433542321654321HGGHGGHGGHGGGGGG))((35423232HGGHGGLLLLji325432HHGGGG不存在kjiLLL利用梅森公式求传递函数(1)32543244335423216543214111HHGGGGHGGHGGHGGHGGGGGGLLLLLLikjijii利用梅森公式求传递函数(2)kkP,.2求6543211GGGGGGP?1求余子式1G1H1H2H3G6H4G5G4G3G2R(s)C(s)----1234将第一条前向通道从图上除掉后的图,再用特征式的求法,计算1求余式1将第一条前向通道从图上除掉后的图图中不再有回路,故1=1G1H1H2H3G6H4G5G4G3G2R(s)C(s)----1234G1H1H2H3G6H4G5G4G3G2R(s)C(s)----1234利用梅森公式求传递函数(3)RC求总传递函数.311PRC32543244335423216543216543211HHGGGGHGGHGGHGGHGGGGGGGGGGGG例2:用梅森公式求传递函数试求如图所示的系统的传递函数。G1H1H2G4G3G2RC求解步骤之一:确定反馈回路G1H1H2G4G3G2RC3211GGGL求解步骤之一:确定反馈回路1212HGGLG1H1H2G4G3G2RC求解步骤之一:确定反馈回路2323HGGLG1H1H2G4G3G2RC求解步骤之一:确定反馈回路414GGLG1H1H2G4G3G2RC求解步骤之一:确定反馈回路245HGLG1H1H2G4G3G2RC求解步骤之二:确定前向通路G1H1H2G4G3G2RC3211GGGP11求解步骤之二:确定前向通路G1H1H2G4G3G2RC412GGP2n前向通路数:12求解步骤之三:求总传递函数2441232121321413211HGGGHGGHGGGGGGGGGGRC例3:对例2做简单的修改G1H1H2G4G3G2RC①求反馈回路1G1H1H2G4G3G2RC3211GGGL②求反馈回路2G1H1H2G4G3G2RC1212HGGL③求反馈回路3G1H1H2G4G3G2RC2323HGGL④求反馈回路4G1H1H2G4G3G2RC44GL2.①两两互不相关的回路1G1H1H2G4G3G2RC))((121442HGGGLL②两两互不相关的回路2G1H1H2G4G3G2RC))((232443HGGGLL3.①求前向通路1G1H1H2G4G3G2RC3211GGGP113.②求前向通路2G1H1H2G4G3G2RC42GP2n前向通路数:12121HGG232HGG4.求系统总传递函数3211GGGL1212HGGL2323HGGL44GL))((121442HGGGLL))((232443HGGGLL3211GGGP1142GP12121HGG232HGG4342432122111LLLLLLLLPPRC脉冲响应函数即脉冲过渡函数,就是系统对单位脉冲函数输入的响应,用k(t)表示。()t2-5系统的脉冲响应函数由此可知系统(或元件)的传函的拉氏反变换就等于它的脉冲响应。设系统传函为,而所以有()s()1,()()LtLktKs()()/1()sKsKs11()()()ktLKsLs概念和定义返回子目录对于任意输入信号r(t),系统输出为c(t),则()()()()()CssRsKsRs用拉氏变换的卷积定理可得:0()()()tctrktd由此可知,对于线性系统,只要知道它的脉冲过渡函数k(t),就可以计算出系统对任意输入信号r(t)的时间响应过程c(t)。(251)注:传递函数简称传函(下同)下面用线性系统的叠加原理说明式(2-5-1)的物理含义设任意输入信号r(t),如上图所示,分成一系列宽度为的相邻矩形脉冲。则一矩形脉冲可表为t()()rntttnt(252)式中是发生在时刻的理想脉冲。则式表示的矩形脉冲引起的系统输出为,由物理系统的因果关系,可知当时,有。由叠加原理得:()tnttnt(252)()()rnttktnttnt()0ktnt0()()()tntctrntktntt当时,记,上式可写为0t,tdnt0()()()tctrktd当系统输入为单位阶跃信号时,则单位阶跃响应记作h(t),由(2-5-1)式得00()1()()()tthtktdkd所以知道系统的脉冲响应,就可以惟一确定其单位阶跃响应,反之亦然,即()()dhtktdt2-6典型反馈系统传递函数G1(s)G2(s)H(s)RCNBE输入:控制输入干扰输入输出:由控制作用产生的输出由干扰作用产生的输出返回子目录一、系统开环传递函数)()()()(21sHsGsGsGG1(s)G2(s)H(s)RCNBE不含极性闭环系统的开环传递函数为:它是当主反馈回路断开时反馈信号B(s)与输入信号之间的传递函数。二、系统在r(t)作用下的闭环传递函数•令n(t)=0G1(s)G2(s)H(s)RCBE为:递函数作用下,系统的闭环传在)()(strHGGGGsRsCs21211)()()()(1)()()(2121sRHGGGGsRssC注:该系统为负反馈系统,系统传函中分母为1+开环传递函数,反之,若主反馈为正反馈时,则系统传函为1-开环传函三、系统在n(t)作用下的闭环传递函数•令r(t)=0G1(s)G2(s)H(s)NC函数为:作用下的系统闭环传递干扰)(tnHGGGsNsCsn2121)()()()(1)()()(212sNHGGGsNssCn四、系统总输出线性系统满足叠加原理。系统总输出的拉氏变换式为:)()()()()(sRssNssCn)()()(1)()()()()(21221sHsGsGsNsGsRsGsG五、闭环系统的误差传递函数•按上图规定误差为:G1(s)G2(s)H(s)RCNBEe(t)=r(t)-b(t)E(s)=R(s)-B(s)1.r(t)作用下的系统误差传递函数()ers此时令n(t)=0,则结构图如下所示12()1()()1()()()erEssRsGsGsHs此时令n(t)=0,则结构图如下所示2.n(t)作用下的系统误差传递函数()ens212()()()()()1()()()enGsHsEssNsGsGsHs3.系统总误差21212()()()()()()()1()()1()()()1()()()erenEssRssNsGsHsRsNsGsGsHsGsGsHsG1(s)G2(s)H(s)RCNBE六、闭环系统的特征方程式无论是系统传递函数还是误差传递函数,它们都有一个共同的特点,拥有相同的分母,这就是闭环系统的本质特征,我们将闭环传递函数的分母多项式称为闭环系统的特征方程式。它与输入无关,仅与系统本身的结构和参数有关。本章引入了传递函数这一基本概念,概念的引入过程、所介绍的主要内容以及这些内容间的关系可以用示意图表示如下:考虑负载效应拉氏变换(零初条件)(零初条件)(零初条件)拉氏变换消元法抽象物理、化学定律简化假定克莱姆法则线性化方法自动控制系统物理模型系统部件微分方程组系统增量动态方程组系统象函数方程组系统动态结构图(信号流图)梅森公式结构图等效变换法则C(s)系统原理方块图系统输入输出动态关系式传递函数传递函数概念与后几章的关系可用下图来表示。传递函数单位脉冲响应函数第三章时域分析第四章根轨迹法第五章频率域分析拉氏反变换sj第3章时域分析法3-1时域分析基础3-2一、二阶系统分析与计算3-3系统稳定性分析3-4稳态误差分析计算基本要求返回主目录基本要求1熟练掌握一、二阶系统的数学模型和阶跃响应的特点。熟练计算性能指标和结构参数,特别是一阶系统和典型欠阻尼二阶系统动态性能的计算方法。2了解一阶系统的脉冲响应和斜坡响应的特点。3正确理解系统稳定性的概念,能熟练运用稳定性判据判定系统的稳定性并进行有关的参数计算、分析。返回子目录4正确理解稳态误差的概念,明确终值定理的应用条件。5熟练掌握计算稳态误差的方法。6掌握系统的型次和静态误差系数的概念。控制系统的数学模型是分析、研究和设计控制系统的基础,经典控制论中三种分析(时域,根轨迹,频域)、研究和设计控制系统的方法,都是建立在这个基础上的。3-1时域分析基础一、时域分析法的特点它根据系统微分方程,通过拉氏变换,直接求出系统的时间响应。依据响应的表达式及时间响应曲线来分析系统控制性能,并找出系统结构、参数与这些性能之间的关系。这是一种直接方法,而且比较准确,可以提供系统时间响应的全部信息。返回子目录二、典型初始状态,典型外作用1.典型初始状态通常规定控制系统的初始状态为零状态。即在外作用加于系统之前,被控量及其各阶导数相对于平衡工作点的增量为零,系统处于相对平衡状态。2.典型外作用①单位阶跃函数1(t)tf(t)00t00t1)t(1)t(f其拉氏变换为:s1dte1)s(F)]t(f[L0st其数学表达式为:t②单位斜坡函数0t0t0t)t(1t)t(f其拉氏变换为:20sts1dtet)s(F)]t(f[Lf(t)0其数学表达式为:③单位脉冲函数000)()(ttttf其数学表达式为:其拉氏变换为:1)()]([sFtfL1)(dtt定义:图中1代表了脉冲强度。单位脉冲作用在现实中是不存在的,它是某些物理现象经数学抽象化的结果。④正弦函数其拉氏变换为:220sin)()]([ωsωdteωtsFtfLst000sin)(ttωttf其数学表达式为:f(t)三、典型时间响应初状态为零的系统,在典型输入作用下输出量的动态过程,称为典型时间响应。1.单位阶跃响应定义:系统在单位阶跃输入[r(t)=1(t)]作用下的响应,常用h(t)表示。()s若系统的闭环传函为,则h(t)的拉氏变换为1()()htLHs故1()()()()HssRsss(311)2.单位斜坡响应定义:系统在单位斜坡输入[r(t)=t·1(t)]作用下的响应,常用表示。()tct故1()()ttctLCs则有21()()()()tCssRsss(312)3.单位脉冲响应定义:系统在单位脉冲输入r(t)=δ(t)作用下的响应,常用k(t)表示。注:关于正弦响应,将在第五章里讨论故11()()()ktLKsLs则有()()()()1()KssRsss(313)4.三种响应之间的关系由式(3-1-3)可将式(3-1-1)和式(3-1-2)写为:11()()()HssKsss22111()()()()tCssKsHssss相应的时域表达式为0()()thtkd0()()ttcthd四、阶跃响应的性能指标t)(th)(pth1ptst误差带01、峰值时间tp:指h(t)曲线中超过其稳态值而达到第一个峰值所需的时间。2、超调量%:指h(t)中对稳态值的最大超出量与稳态值之比。3、调节时间ts:指响应曲线中,h(t)进入稳态值附近5%h()或2%h()误差带,而不再超出的最小时间。4、稳态误差ess:指响应的稳态值与期望值之差。注意事项:。%和而没有稳态误差入,则只有而言的,对于非阶跃输应三项指标是针对阶跃响及ssssssteet,%,3-2一、二阶系统分析与计算定义:由一阶微分方程描述的系统称为一阶系统。一、一阶系统的数学模型及单位阶跃响应返回子目录一阶系统数学模型微分方程:动态结构图:传递函数:)()()(trtcdttdcT11)()(TssRsCTs1)(sR)(sC一阶系统单位阶跃响应输入:输出:)(1)(ttrssR1)(sTssRssC111)()()(TtetC1)(单位阶跃响应曲线初始斜率:0()1tdhtdtT性能指标1.平稳性:2.快速性ts:3.准确性ess:非周期、无振荡,=0]%5[95.0)(3误差带对应时,tcTt]%2[98.0)(4误差带对应时,tcTt0)(1cess举例说明(一阶系统)一阶系统如图所示,试求:1.当KH=0.1时,求系统单位阶跃响应的调节时间ts,放大倍数K,稳态误差ess;2.如果要求ts=0.1秒,试问系统的反馈系数KH应调整为何值?3.讨论KH的大小对系统性能的影响及KH与ess的关系。看懂例题3-1并回答上述各题s100)(sR)(sCHK)(sE)(sB100sHK二、二阶系统的数学模型及单位阶跃响应定义:由二阶微分方程描述的系统称为二阶系统。二阶系统数学模型二阶系统的微分方程一般式为:阻尼比无阻尼振荡频率n2222()()2()()nnndctdctctrtdtdt(0)n二阶系统的反馈结构图)2(2nnss)(sR)(sC2(2)nnss二阶系统的传递函数开环传递函数:222()()2nnnCsRsss2()(2)nnGsss闭环传递函数:二阶系统的特征方程为2220nnss解方程求得特征根:当输入为阶跃信号时,则微分方程解的形式为:12012()ststctAAeAe式中为由r(t)和初始条件确定的待定的系数。012,,AAAs1,s2完全取决于,n两个参数。21,21nns此时s1,s2为一对共轭复根,且位于复平面的左半部。01①特征根分析—(欠阻尼21,21nnssj②特征根分析—(临界阻尼)此时s1,s2为一对相等的负实根。s1=s2=-n21,21nnns1⑷特征根分析—(过阻尼)此时s1,s2为两个负实根,且位于复平面的负实轴上。21,21nns1⑤特征根分析—(零阻尼)此时s1,s2为一对纯虚根,位于虚轴上。S1,2=jn21,21nnnsj0⑥特征根分析—(负阻尼)此时s1,s2为一对实部为正的共轭复根,位于复平面的右半部。21,21nnsj10⑦特征根分析—(负阻尼)此时s1,s2为两个正实根,且位于复平面的正实轴上。21,21nns1二阶系统单位阶跃响应21111/nnsT1.过阻尼二阶系统的单位阶跃响应22211/nnsT21212111()()()(1)(1)nCssssssTsTss取C(s)拉氏反变换得:1211211211()1,(0)/1/1ttTThteetTTTT(314)(1)过阻尼系统分析衰减项的幂指数的绝对值一个大,一个小。绝对值大的离虚轴远,衰减速度快,绝对值小的离虚轴近,衰减速度慢;衰减项前的系数一个大,一个小;二阶过阻尼系统的动态响应呈非周期性,没有振荡和超调,但又不同于一阶系统;离虚轴近的极点所决定的分量对响应产生的影响大,离虚轴远的极点所决定的分量对响应产生的影响小,有时甚至可以忽略不计。过阻尼系统单位阶跃响应tc(t)0与一阶系统阶跃响应的比较tc(t)0二阶过阻尼系统一阶系统响应1二阶过阻尼系统阶跃响应指标分析0.2%响应没有振荡0)]()([lim.1tctretss误差对于过阻尼二阶系统的响应指标,只着重讨论,它反映了系统响应过渡过程的长短,是系统响应快速性的一个方面,但确定的表达式是很困难的,一般根据(3-1-4)取相对量及经计算机计算后制成曲线或表格。stst1/stT12/TT2.欠阻尼二阶系统的单位阶跃响应(01)21,21nnsjdj222()()2nnnCsRsssn为根的实部的模值;21dn为阻尼振荡角频率二阶欠阻尼系统的输出2221()2nnncssss22221()()nnndndssss拉氏反变换得:2()1[cos(sin)]1ntddctett21()1sin(arccos)1ntdctet二阶欠阻尼系统输出分析二阶欠阻尼系统的单位阶跃响应由稳态分量和暂态分量组成。稳态分量值等于1,暂态分量为衰减过程,振荡频率为ωd。下图为二阶系统单位阶跃响应的通用曲线。下面根据上图来分析系统的结构参数、对阶跃响应的影响n•平稳性(%)21nteA暂态分量的振幅为:结论:越大,ωd越小,幅值也越小,响应的振荡倾向越弱,超调越小,平稳性越好。反之,越小,ωd越大,振荡越严重,平稳性越差。21dn振荡角频率为:当=0时,为零阻尼响应,具有频率为的不衰减(等幅)振荡。n阻尼比和超调量的关系曲线如下图所示21dn结论:对于二阶欠阻尼系统而言,大,小,系统响应的平稳性好。n•在一定的情况下,越大,振荡频率也越高,响应平稳性也越差。nd•快速性从图中看出,对于5%误差带,当时,调节时间最短,即快速性最好。同时,其超调量<5%,平稳性也较好,故称为最佳阻尼比。0.7070.707总结:越大,调节时间越短;当一定时,越大,快速性越好。nstn•稳态精度21()1sin(arccos)1ntdhtet从上式可看出,瞬态分量随时间t的增长衰减到零,而稳态分量等于1,因此,上述欠阻尼二阶系统的单位阶跃响应稳态误差为零。欠阻尼二阶系统单位阶跃响应性能指标1.上升时间:令,则st()1rht211sin(arccos)11ntdet所以:arccosrdt根据极值定理有:0)(pttdttdc该项不可能为零2sin1npt21nptne02.峰值时间:pt2sin10npt21(01,2)nptnn,取n=1得:21pdnt3.超调量:%将峰值时间代入下式/pdt21()1sin(arccos)1ntdhtet得:22/1/1max2()()1sin(arccos)11pehthte所以:2/1()()%100%100%()phtheh4.调节时间st写出调节时间的表达式相当困难。在分析设计系统十,经常采用下列近似公式。当阻尼比时0.83.5(snt取5%误差带)4.5(snt取2%误差带)三、二阶系统举例2设位置随动系统,其结构图如图所示,当给定输入为单位阶跃时,试计算放大器增益KA=200,1500,13.5时,输出位置响应特性的性能指标:峰值时间tp,调节时间ts和超调量,并分析比较之。)5.34(5ssKARC例题解析(1)•输入:单位阶跃)(1)(ttrssR1)(系统的闭环传递函数:AAKssKs55.345)(2例题解析(2)当KA=200时10005.341000)(2sss系统的闭环传递函数:与标准的二阶系统传递函数对照得:34.50.5452n20.121pdnt峰值时间:秒2113%e超调量:%3.00.17snt调节时间:秒6.311000n1rads例题解析(3)当KA=1500时75005.3415005)(2sss系统的闭环传递函数:与标准的二阶系统传递函数对照得:6.867500n34.50.22n20.03784.851pnt峰值时间:秒2152.7%e超调量:%3.00.17snt调节时间:秒1rads例题解析(4)当KA=13.5时5.675.345.67)(2sss系统的闭环传递函数:与标准的二阶系统传递函数对照得:21.85.67n34.52.12n?pt峰值时间:0%超调量:1(6.451.7)1.44snt调节时间:秒无1rads系统在单位阶跃作用下的响应曲线c(t)10tKA=1500KA=200KA=13.5四改善二阶系统响应的措施1.误差信号的比例-微分控制系统开环传函为:2(1)()()()(2)ndnTsCsGsEsss闭环传函为:2222(1)()()()(2)ndndnnTsCssRssTs等效阻尼比:12ddnT可见,引入了比例-微分控制,使系统的等效阻尼比加大了,从而抑制了振荡,使超调减弱,可以改善系统的平稳性。微分作用之所以能改善动态性能,因为它产生一种早期控制(或称为超前控制),能在实际超调量出来之前,就产生一个修正作用。前面图的相应的等效结构由此知道:12()()()ctctct和及的大致形状如下1()ct2()ct()ct一方面,增加项,增大了等效阻尼比,使曲线比较平稳。另一方面,它又使加上了它的微分信号,加速了c(t)的响应速度,但同时削弱了等效阻尼比的平稳作用。dTd1()ct1()ct2()ctd总结:引入误差信号的比例-微分控制,能否真正改善二阶系统的响应特性,还需要适当选择微分时间常数。若大一些,使具有过阻尼的形式,而闭环零点的微分作用,将在保证响应特性平稳的情况下,显著地提高系统的快速性。dTdT1()ct2.输出量的速度反馈控制将输出量的速度信号c(t)采用负反馈形式,反馈到输入端并与误差信号e(t)比较,构成一个内回路,称为速度反馈控制。如下图示。闭环传函为:2222()()()(2)nntnnCssRssKs等效阻尼比:12ttnK等效阻尼比增大了,振荡倾向和超调量减小,改善了系统的平稳性。3.比例-微分控制和速度反馈控制比较从实现角度看,比例-微分控制的线路结构比较简单,成本低;而速度反馈控制部件则较昂贵。从抗干扰来看,前者抗干扰能力较后者差。从控制性能看,两者均能改善系统的平稳性,在相同的阻尼比和自然频率下,采用速度反馈不足之处是其会使系统的开环增益下降,但又能使内回路中被包围部件的非线性特性、参数漂移等不利影响大大削弱。五高阶系统的时域分析定义:用高阶微分方程描述的系统称为高阶系统。由于求高阶系统的时间响应很是困难,所以通常总是将多数高阶系统化为一、二阶系统加以分析。通常对于高阶系统来说,离虚轴最近的一个或两个闭环极点在时间响应中起主导作用,而其他离虚轴较远的极点,他们在时间响应中相应的分量衰减较快,只起次要作用,可以忽略。这时,高阶系统的时域分析就转化为相应的一、二阶系统。这就是所谓的主导极点的概念,将在第四章中详细介绍。一、二阶系统的极点分布如下:3-3系统稳定性分析本节主要内容:线性定常系统稳定的概念系统稳定的条件和稳定性的判定方法。返回子目录一、系统稳定的概念是指系统当扰动作用消失后,由初始偏差状态恢复到原平衡状态的性能。若系统能恢复平衡状态,就称该系统是稳定的,若系统在扰动作用消失后不能恢复平衡状态,且偏差越来越大,则称系统是不稳定的。二、稳定性的数学条件设系统的线形化增量方程为:)()()()()()()()(1111011110trbdttdrbdttrdbdttrdbtcadttdcadttcdadttcdammmmmmnnnnnn对上式进行拉氏变换得:)()()()()(011101110sMsRbsbsbsbsCasasasammmmnnnn其中:D(s)为系统闭环特征式,也称输出端算子式;M(s)称为输入端算子式。R(s)为输入,C(s)为输出,M0(s)为总的初始条件,与系统的初始状态有关的多项式。或简写为:0()()()()()DsCsMsRsMs则有:)()()()()()(0sDsMsRsDsMsC假定:01()()niiiDsasss其中互异。将C(s)等式右的两项分别展开成部分分式,可得0111()nlnjiiijiirjiBACCsssssss再进行拉氏反变换,得)(tcnitsiieC1tsniiieA1该部分为稳态分量,即微分方程的特解,取决于输入作用。1rjlstjjBe)(tcnitsiieC1tsniiieA11rjlstjjBe该为瞬态分量,即微分方程的通解,运动规律取决于,由系统的结构参数确定。is系统去掉扰动后的恢复能力,应由瞬态分量决定。此时,系统的输入为零。故:稳定性定义可转化为:式中:Ai,Ci均为常值,因此,系统的稳定性仅取决于特征根si的性质。01lim()0instiitiACe特征根的性质对系统稳定性的影响当si为实根时,即si=i,时:0itsiitieCA)(lim0时:0itsiitieCA)(limiiCA时:0itsiitieCA)(lim0i0i0it0)(tciiCA特征根与系统稳定性的关系(2)当si为共轭复根时,即si,i+1=i±jωi])()[(lim)(11)(tjiitjiitiiiieCAeCA])()[(lim11tjiitjiittiiieCAeCAe)sin(limiitttAei则若,0i0)sin(limiitttAei则若,0i则若,0i)sin()sin(limiiiitttAtAei)sin(limiitttAei共轭复根情况下系统的稳定性结论:系统稳定的充分必要条件是:系统的特征方程的所有根都具有负实部,或者说都位于S平面的虚轴之左。注:拉氏变换性质中的终值定理的适用条件:SE(S)在S平面的右半平面解析,就是上面稳定条件的另一种表示,即特征方程的所有根Si位于S平面的虚轴之左。三、稳定性判据判据之一:赫尔维茨(Hurwitz)稳定判据系统稳定的充分必要条件是:特征方程的赫尔维茨行列式Dk(k=1,2,3,…,n)全部为正。赫尔维茨判据系统特征方程的一般形式为:0)(1110nnnnasasasasD各阶赫尔维茨行列式为:00aD11aD20312aaaaD3142053130aaaaaaaaDnnnnnnaaaaaaaaaaaaaaaD00000422032312242012531(一般规定)00a举例:系统的特征方程为:010532234ssss试用赫尔维茨判据判断系统的稳定性。解:第一步:由特征方程得到各项系数0a1a2a3a4a2135第二步:计算各阶赫尔维茨行列式200aD111aD20312aaaaD3251752310结论:系统不稳定。10010532)(234sssssD三、稳定性判据判据之二:林纳德-奇帕特(Lienard-Chipard)判据系统稳定的充分必要条件为:1.系统特征方程的各项系数大于零,即),,2,1,0(0niai2.奇数阶或偶数阶的赫尔维茨行列式大于零。即0偶D0奇D或必要条件举例:单位负反馈系统的开环传递函数为:)125.0)(11.0()(sssKsG试求开环增益K的稳定域。解:第一步:求系统的闭环特征方程0)125.0)(11.0()(KssssD035.0025.023Ksss第二步:列出特征方程的各项系数。025.00a35.01a12aKa3第三步:系统稳定的充分必要条件。,0)1(ia0K要求0)2(2D20312aaaaD即:1025.035.0K0025.035.0K解得:K<14开环增益K的稳定域为:140K由此例可见,K越大,系统的稳定性越差。上述判据不仅可以判断系统的稳定性,而且还可根据稳定性的要求确定系统参数的允许范围(即稳定域)。三、稳定性判据判据之三:劳斯(Routh)判据系统稳定的充分必要条件是:劳斯表中第一列所有元素的计算值均大于零。若系统的特征方程为:01110nnnnasasasa则劳思表中各项系数如下图:1302113aaaaac2ns1504123aaaaac1706133aaaaac3ns1323131314ccaacc1313351324cacacc2s1,1nc1,2ncnc,10snnac1,1024611357nnsaaaasaaaas关于劳斯判据的几点说明如果第一列中出现一个小于零的值,系统就不稳定;如果第一列中有等于零的值,说明系统处于临界稳定状态;第一列中数据符号改变的次数等于系统特征方程正实部根的数目,即系统中不稳定根的个数。例1设系统特征方程如下:05432234ssss试用劳斯判据判断该系统的稳定性,并确定正实部根的数目。解:将特征方程系数列成劳斯表4s1353s2402s24132120152501s15241600s5结论:系统不稳定;系统特征方程有两个正实部的根。05432234ssss劳斯表判据的特殊情况在劳斯表的某一行中,第一列项为零。在劳斯表的某一行中,所有元素均为零。在这两种情况下,都要进行一些数学处理,原则是不影响劳斯判据的结果。例2设系统的特征方程为:0433ss试用劳斯判据确定正实部根的个数。解:将特征方程系数列成劳斯表321104sss-3由表可见,第二行中的第一列项为零,所以第三行的第一列项出现无穷大。为避免这种情况,可用因子(s+a)乘以原特征式,其中a可为任意正数,这里取a=1。3340ss于是得到新的特征方程为:043)1)(43(2343sssssss将特征方程系数列成劳斯表:43210134114424sssss结论:第一列有两次符号变化,故方程有两个正实部根。例3设系统的特征方程为:试用劳思判据确定正实部根的个数。65432237440ssssss解:将特征方程系数列成劳斯表65432237440ssssss劳思表中出现全零行,表明特征方程中存在一些大小相等,但位置相反的根。这时,可用全零行上一行的系数构造一个辅助方程,对其求导,用所得方程的系数代替全零行,继续下去直到得到全部劳思表。65431-2-7-4s1-3-4s1-3-4s000s用行的系数构造系列辅助方程4s42F(s)=s34s求导得:用上述方程的系数代替原表中全零行,然后按正常规则计算下去,得到3()460dFsssds65432101-2-7-4s1-3-4s1-3-4s4-60s-1.5-4s-16.70s-4s65432237440ssssss65431-2-7-4s1-3-4s1-3-4s000s3()460dFsssds表中的第一列各系数中,只有符号的变化,所以该特征方程只有一个正实部根。求解辅助方程,可知产生全零行的根为。再可求出特征方程的其它两个根为。(-1j3)/22,j四.结构不稳定及改进措施某些系统,仅仅靠调整参数仍无法稳定,称结构不稳定系统。如下图液位可能控制系统。消除结构不稳定的措施有两种①改变积分性质②引入比例-微分控制,补上特征方程中的缺项。该系统的闭环特征方程为:32100mpmTssKKKK系数缺项,显然不满足系统稳定的必要条件,且无论怎么调整系统参数,都不能使系统稳定。1.改变积分性质用反馈包围积分环节或者包围电动机的传递函数,破坏其积分性质。HK2010HXsKXssKK211mmmHXsKXsTssKK2.引入比例-微分控制在原系统的前向通路中引入比例-微分控制。20111mHsKsHssTsKs其闭环特征方程为:023KsKssTm由稳定的充分必要条件:引入比例-微分控制后,补上了特征方程中s的一次项系数。只要适当匹配参数,满足上述条件,系统就可以稳定。221203,0,,0,0immaKDDaaaaKKTTm则T均大于零;故3-4稳态误差分析计算一.误差与稳态误差系统的误差e(t)常定义为:e(t)=期望值-实际值误差:(1)e(t)=r(t)-c(t)(2)e(t)=r(t)-b(t)返回子目录稳态误差定义:稳定系统误差的终值称为稳态系统。当时间t趋于无穷时,e(t)极限存在,则稳态误差为teetsslim二.稳态误差的计算若e(t)的拉普拉斯变换为E(s),且0lim()lim()sstseetsEs=0lim(),lim()tsetsEs存在,则有0lim(),lim()tsetsEs在计算系统误差的终值(稳态误差)时,遇到的误差的象函数一般是s的有理分式函数,这时当且仅当的极点均在左半面,就可保证()sEs()Es存在,式就成立。注:sE(s)的极点均在左半面的条件中,蕴涵了闭环系统稳定的条件。0lim()lim()sstseetsEs=对上述系统,若定义e(t)=r(t)-b(t),则E(s)=R(s)-B(s)()()()()()()()()()BRBNBRBNBssRssNsssBsNs其中为B(s)对R(s)的闭环传函,为对干扰信号的闭环传函。E()()()()()()()]()()()BRBNBRBNsRssRssNssRssNs从而得=[1-121212()()()1()1()1()()()1()()()BRERGsGsHsssGsGsHsGsGsHs1-称之为系统对输入信号的误差传递函数。212()()()()1()()()BNENGsHsssGsGsHs称为系统对干扰的误差传递函数。()ENs000lim()lim()lim()ssRNssrssnsssesEssEssEsee若具备应用终值定理条件,则()()()()()ERENEssRssNs综合上述各式有:例:系统结构如下图。当输入信号r(t)=1(t),干扰n(t)=1(t)时,求系统的总的稳态误差sse解:①判别稳定性。由于是一阶系统,所以只要参数大于零,系统就稳定。12,KK②求E(s)。()()()()()ERENEssRssNs根据结构图可以求出:121()1()ERssGssKK212()()ENCNKsssKK依题意:R(s)=N(s)=1/s,则2121211()KsEssKKssKKs③应用终值定理得稳态误差sse20012121111lim()lim[]ssssKsesEsssKKssKKsK三输入信号作用下的稳态误差与系统结构参数的关系•当系统只有输入r(t)作用时,系统的开环传递函数为:)(sGREC)(sHB)()()()(sHsGsEsB将G(s)H(s)写成典型环节串联形式:为积分环节的个数。为开环增益;式中,K0R00()E(s)=E()()()()()()ERsDsssRsRssDsKNs求得:当sE(s)的极点全部在s平面的左半平面时,可用终值定理求得:100000()lim()lim()()()sssssDsesEsRssDsKNs上式表明:系统的稳态误差除与输入有关外,只与系统的开环增益K和积分环节的个数有关。22'0122221220()(1)(21)()()(1)(21)()KNsKsssGsHssTsTsTssDs1.阶跃信号作用下的稳态误差)(1)(0trtrsrsR0)(Kress100时,当01sse时,当02sse时,当要消除阶跃信号作用下的稳态误差,开环传递函数中至少要有一个积分环节。但是,积分环节多会导致系统不稳定。10000000000()()limlim()()()()sssssDsrsDsresDsKNsssDsKNs2.斜坡信号作用下的稳态误差)(1)(0ttVtr20)(sVsR0sse当时,KVess01时,当02sse时,当要消除斜坡信号作用下的稳态误差,开环传递函数中至少要有两个积分环节。1100002000000()()limlim()()()()sssssDsVsDseVsDsKNsssDsKNs3.等加速信号作用下的稳态误差)(12)(20ttatr30)(sasR0sse当时,1sse当时,Kaess02时,当要消除等加速信号作用下的稳态误差,开环传递函数中至少要有三个积分环节。但是,积分环节多会导致系统不稳定。1200003000000()()limlim()()()()sssssDsasDseasDsKNsssDsKNs由以上分析可见,要消除系统在幂函数输入信号作用下的稳态误差,则要求增加积分环节的数目,要减小系统的稳态误差,则要求提高开环增益。•系统型别是针对系统的开环传递函数中积分环节的个数而言的。=0的系统称为0型系统;=1的系统称为Ⅰ型系统;=2的系统称为Ⅱ型系统;例:系统结构如下图:若输入信号为21()12rttt试求系统的稳态误差。解:①判别稳定性。系统的闭环特征方程为232111(1)(1)00mmmmmsTsKKsTssKKsKK1mmmTKKT稳定条件:(1),,,均应大于零;(2)②根据系统结构与稳态误差之间的关系,可以直接求sse从结构图看出,该系统为单位反馈且属Ⅱ型系统。因此12203112310()011ssssssmssssssssmertteateKKKeeeeKK当输入r(t)=1(t)时,;当输入时,;1当输入r(t)=时,2所以系统的稳态误差注意事项系统必须是稳定的,否则计算稳态误差没有意义;以上结论仅适用于输入信号作用下系统的稳态误差,不适用于干扰作用下系统的稳态误差;上述公式中K必须是系统的开环增益,也即开环传递函数中,各典型环节的常数项均为1时的系数。以上规律是根据误差定义E(s)=R(s)-B(s)推得的。四干扰作用下的稳态误差与系统结构参数的关系用一待定的来代替上图中的,然后找出消除系统在干扰n(t)作用下的误差时,需具备的条件。1()Gs1K1()Gs12012()()lim[()],()()NssnsGssEssKesNsntsGsK选择首先要保证的所有极点在平面的左半平面。这时当为单位阶跃干扰时,有2012,lim[]()ssnsKesGsK1N(s)=则s111212100121112()(1)(1)(),(1)(1)(1)(1)lim[]lim()(1)(1)(1)(1)hkkssnsskhsKssssTsTsKsTsTsKesGsKsTsTsKssK11设G具有以下形式G则10,()1sseGs要使则中至少要有一个积分环节,即111(1)()(0,0)KsGsKs为保证系统稳定,取在满足稳定性前提下,就可使系统在阶跃干扰作用下的稳态误差为零。以上分析表明,是误差信号到干扰作用点之间的传递函数,系统在时间幂函数干扰作用下的稳态误差与干扰作用点到误差信号之间的积分环节数目和增益大小有关,而与干扰干扰作用点后面的积分环节数目和增益大小无关。1()Gsssne例:系统结构图如下,已知干扰n(t)=1(t),试求干扰作用下的稳态误差解:①判断稳定性。系统开环传函为ssne121212(1)()(1)KKTsGssTTs所以闭环特征方程为32212121/0TssKKsKKT1212121,,,2TTKKTT稳定条件:()均应大于零。()②求稳态误差ssne从图中可以看出,误差信号到干扰作用点之前的传递函数中含有一个积分环节,所以可得出,系统在阶跃干扰作用下的稳态误差为零。ssne22212110()(1)(/)(1)lim()sKsssTsKKTTsssENssnEN实际上在满足稳定性的条件下,因N(s)=1/s,所以有eN(s)=0本章知识点及联系误差的定义公式、图线公式、图线劳斯判据、赫尔维茨判据()Gs()s()es,n,K,,pstt%Tsse一阶系统标准式二阶系统标准式闭环特征式稳定性()Es终值定理判稳等效单位负反馈系统开环传递函数,,pvaKKK()Hs判稳误差系数4210011001010101101000101001011第四章根轨迹法4210011001010101101000101001011第4章根轨迹法基本要求4-1根轨迹与根轨迹方程4-2绘制根轨迹的基本法则4-3广义根轨迹4-4系统闭环零、极点分布与阶跃响应的关系4-5系统阶跃响应的根轨迹返回主目录4210011001010101101000101001011基本要求1.正确理解开环零、极点和闭环零、极点以及主导极点、偶极子等概念。2.正确理解和熟记根轨迹方程(模方程及相角方程)。熟练运用模方程计算根轨迹上任一点的根轨迹增益和开环增益。3.正确理解根轨迹法则,法则的证明只需一般了解,熟练运用根轨迹法则按步骤绘制反馈系统开环增益K从零变化到正无穷时的闭环根轨迹。返回子目录42100110010101011010001010010114.正确理解闭环零极点分布和阶跃响应的定性关系,初步掌握运用根轨迹分析参数对响应的影响。能熟练运用主导极点、偶极子等概念,将系统近似为一、二阶系统给出定量估算。5.了解绘制广义根轨迹的思路、要点和方法。4210011001010101101000101001011根轨迹法根轨迹法根据反馈控制系统的开、闭环传递函数之间的关系,直接由开环传递函数零、极点求出闭环极点(闭环特征根)。这给系统的分析与设计带来了极大的方便。闭环控制系统的稳定性和性能指标主要由闭环系统极点在复平面的位置决定,因此,分析或设计系统时确定出闭环极点位置是十分有意义的。4210011001010101101000101001011定义:根轨迹是指系统开环传递函数中某个参数(如开环增益K)从零变到无穷时,闭环特征根在s平面上移动的轨迹。4-1根轨迹与根轨迹方程•当闭环系统为正反馈时,对应的轨迹为零度根轨迹;而负反馈系统的轨迹为根轨迹。180一、根轨迹返回子目录4210011001010101101000101001011例子•如图所示二阶系统,系统的开环传递函数为:()(0.51)KGsss4210011001010101101000101001011•开环传递函数有两个极点。没有零点,开环增益为K。120,2pp•闭环特征方程为2()220DsssK•闭环特征根为12112,112sKsK闭环传递函数为2()2()()22CsKsRsssK4210011001010101101000101001011从特征根的表达式中看出每个特征根都随K的变化而变化。例如,设K=0K=0.5K=1K=2.5K=+∞12121212120,21,11,112,121,1sssssjsjsjsjsjsj4210011001010101101000101001011如果把不同K值的闭环特征根布置在s平面上,并连成线,则可以画出如图所示系统的根轨迹。4210011001010101101000101001011二、闭环零、极点与开环零、极点之间的关系•如图所示系统闭环传递函数为()()1()()GssGsHs(4-4)图4-3控制系统4210011001010101101000101001011•将前向通道传递函数G(s)表示为:22121222122211(1)(21)()(1)(21)()()GfiiGqiiKsssGssTsTsTsszKsp……(4-5)4210011001010101101000101001011为前向通道增益,为前向通道根轨迹增益GKGK式中为反馈通道的根轨迹增益。HK11()()()ljjHhjjszHsKsp(4-7)21222GGKKTT1……(4-6)4210011001010101101000101001011(4-8)11111111()()()()()()()()()()flijijGHqlijiiflijijqhijijszszGsHsKKspspszszKspsp4210011001010101101000101001011闭环传递函数11()()()fhkkGnkkszsKsp,kkzp分别为闭环零、极点。式中:(4-10)4210011001010101101000101001011比较式(4-8)和式(4-10)可得出以下结论①闭环系统根轨迹增益等于系统前向通道的根轨迹增益;②闭环系统零点由前向通道的零点和反馈通道的极点组成;③闭环系统的极点与开环系统的极点、零点以及开环根轨迹增益有关。K根轨迹法的任务是在已知开环零、极点分布的情况下,如何通过图解法求出闭环极点。4210011001010101101000101001011三、根轨迹方程•根轨迹方程G(s)H(s)=-1(4-12)式中G(s)H(s)是系统开环开环传递函数,该式明确表示出开环开环传递函数与闭环极点的关系。•闭环特征方程D(s)=1+G(s)H(s)=0(4-11)闭环极点就是闭环特征方程的解,也称为特征根。4210011001010101101000101001011设开环传递函数有m个零点,n个极点,并假定n≥m,这时式(4-12)又可以写成:11()()()1()miiniiszGsHsKsp(4-13)不难看出,式子为关于s的复数方程,因此,可把它分解成模值方程模值方程和相角方程相角方程。4210011001010101101000101001011相角方程(4-15)11()()(21)0,1,2,mniiiiszspkk111miiniiKszsp模值方程(4-14)4210011001010101101000101001011注意•在实际应用中,用相角方程相角方程绘制根轨迹,而模值方程模值方程主要用来确定已知根轨迹上某一点的值。K•模值方程模值方程不但与开环零、极点有关,还与开环根轨迹增益有关;而相角方程相角方程只与开环零、极点有关。•相角方程相角方程是决定系统闭环根轨迹的充分必充分必要条件要条件。4210011001010101101000101001011例4-1它们应满足相角方程(4-15)2()()2/(2)GsHsKs已知系统的开环传递函数1224,24sjsj试证明复平面上点是该系统的闭环极点。12122,2,ppss若系统闭环极点为证明:该系统的开环极点4210011001010101101000101001011图4-4例4-1开环零、极点分布图4210011001010101101000101001011001112()()9090(21)22spspk(k=0)2s以为试验点,可得1s•以为试验点,观察图4-4,可得图4-41112()()9090(21)22(1)spspkk4210011001010101101000101001011证毕12,ss可见,都满足相角方程,所以,点是闭环极点。12,ss4210011001010101101000101001011例4-2•已知系统开环传递函数当变化时其根轨迹如图4-5所示,求根轨迹上点所对应的K值。4()()/(1)GsHsKs0K10.50.5sjK解根据模值方程求解值410.50.51Kj模值方程图4-5421001100101010110100010100101114K•根据图4-5可得所以20.50.512j图4-54210011001010101101000101001011•上面两个例子说明如何应用根轨迹方程确定复平面上一点是否是闭环极点以及确定根轨迹上一点对应的值。K•根轨迹法可以在已知开环零、极点时,迅速求出开环增益(或其他参数)从零变到无穷时闭环特征方程所有根在复平面上的分布,即根轨迹。42100110010101011010001010010114-2绘制根轨迹的基本法则一、根轨迹的分支数分支数=开环极点数=开环特征方程的阶数二、根轨迹对称于实轴闭环极点为实数→在实轴上复数→共轭→对称于实轴返回子目录4210011001010101101000101001011起于开环极点,终于开环零点。三、根轨迹的起点与终点111)()(Kpszsniimii由根轨迹方程有:4210011001010101101000101001011mnmn若开环零点数m<开环极点数n(有个开环零点在无穷远处)则有()条根轨迹趋于无穷远点0K0ipsips→→起点K0izsizs→→终点4210011001010101101000101001011四、实轴上的根轨迹实轴上根轨迹区段的右侧,开环零、极点数目之和应为奇数。证明:设一系统开环零、极点分布如图。4210011001010101101000101001011在实轴上任取一试验点代入相角方程则3411121()()()()()(21)iiiiszspszszspk所以相角方程成立,即是根轨迹上的点。1s1s4210011001010101101000101001011一般,设试验点右侧有L个开环零点,h个开环极点,则有关系式证毕11()()()lhiiiiszsplh()(21)lhk•如满足相角条件必有所以,L-h必为奇数,当然L+h也为奇数。4210011001010101101000101001011例4-32(1)()(2)KsGsss0K•设一单位负反馈系统的开环传递函数为G(s)=K(s+1)/[s(0.5s+1)],求时的闭环根轨迹。•解:解:将开环传递函数写成零、极点形式•设一单位负反馈系统的开环传递函数为G(s)=K(s+1)/[s(0.5s+1)],求时的闭环根轨迹。4210011001010101101000101001011最后绘制出根轨迹如图4-7所示。①法则一,有两条根轨迹②法则三,两条根轨迹分别起始于开环极点0、-2,一条终于有限零点-1,另一条趋于无穷远处。③法则四,在负实轴上,0到-1区间和-2到负无穷区间是根轨迹。按绘制根规迹法则逐步进行:4210011001010101101000101001011图4-7例4-3根轨迹4210011001010101101000101001011法则五、根轨迹的渐近线•渐近线与实轴正方向的夹角为:mnka)12(渐近线与实轴相交点的坐标为:mnzpnimjjia114210011001010101101000101001011例4-4已知系统的开环传递函数试根据法则五,求出根轨迹的渐近线。12340,4,11,11,4pppjpjn极点解:零点1,1zm2(1)()()(4)(22)KsGsHsssss4210011001010101101000101001011按照公式得12300011(21)(21)(21)41360(0)180(1)300(2)53nmiiiikkknmkkkpznm4210011001010101101000101001011以下是几种开环传递函数的根轨迹渐近线1()Kssp12()()Ksspsp4210011001010101101000101001011123()()()Ksspspsp2123()()()Ksspspsp4210011001010101101000101001011对应的开环传递函数1()()()KGsHsssp(a)12()()()()KGsHssspsp(b)123()()()()()KGsHssspspsp(c)2123()()()()()KGsHssspspsp(d)4210011001010101101000101001011法则六、根轨迹的起始角和终止角根轨迹的终止角是指终止于某开环零点的根轨迹在该点处的切线与水平正方向的夹角。根轨迹的起始角是指根轨迹在起点处的切线与水平正方向的夹角。4210011001010101101000101001011起始角与终止角计算公式•起始角计算公式:终止角计算公式:)()()12(11jmkjjkniikzzzpzkk11(21)()()kmnpkjkijiikkpzpp4210011001010101101000101001011例4-5(2)(2)()()(12)(12)KsjsjGsHssjsj•设系统开环传递函数试绘制系统概略根轨迹。•解将开环零、极点画在图4-12的根平面上,逐步画图:4210011001010101101000101001011图4-12例4-5根轨迹(2)(2)(12)(12)Ksjsjsjsj4210011001010101101000101001011①n=2,有两条根轨迹②两条根轨迹分别起始于开环极点(-1-j2),(-1+j2);终于开环零点(-2-j),(-2+j)③确定起始角,终止角。如图4-13所示。4210011001010101101000101001011例4-5根轨迹的起始角和终止角图4-134210011001010101101000101001011•定义定义:几条(两条或两条以上)根轨迹在s平面上相遇又分开的点。•若根轨迹位于实轴两相邻开环极点之间,则此二极点之间至少存在一个分离点。•若根轨迹位于实轴两相邻开环极点之间,则此二极点之间至少存在一个会合点。七、根轨迹的分离点坐标d4210011001010101101000101001011分离点的坐标d可由下面方程求得nimjjizdpd1111jz式中:为各开环零点的数值,为各开环极点的数值。ip4210011001010101101000101001011例4-62(1)()()33.25KsGsHsss•已知系统的开环传递函数试求闭环系统的根轨迹分离点坐标d,并概略绘制出根轨迹图。4210011001010101101000101001011解:根据系统开环传递函数求出开环极点121.51,1.51pjpj按步骤:①n=2,m=1,有两条根轨迹②两条根轨迹分别起于开环极点,终于开环零点和无穷远零点③实轴上根轨迹位于有限零点-1和无穷零点之间,因此判断有分离点4210011001010101101000101001011④离开复平面极点的初始角为111212180180116.5790206.57206.57pzpppp42100110010101011010001010010111.511.511221(21)21aajjk⑤渐近线121111.511.5112.12,0.12djdjddd(舍去)6、求分离点坐标d4210011001010101101000101001011此系统根轨迹如图4-15所示图4-154210011001010101101000101001011八、分离角与会合角所谓分离角是指根轨迹离开分离点处的切线与实轴正方向的夹角。分离角计算公式mjnliijdsdzdkl11)]()()12[(1(4-45)4210011001010101101000101001011为分离点坐标;d为开环零点;jz个非重根。其它个重极点外,时,除为当lnlkksdi所谓会合角是指根轨迹进入重极点处的切线与实轴正方向的夹角。4210011001010101101000101001011•会合角计算公式ninliiidsdpdkl11)]()()12[(1为分离点坐标;d个非重根。其它个重极点外,时,除为当lnlkksdi现看作开环零点;为原系统的开环极点,ip4210011001010101101000101001011分离角与会合角不必经公式计算,可以用下列简单法则来确定:ll若有条根轨迹进入d点,必有条根轨迹离开d点;ll条进入d点的根轨迹与条离开d点的根轨迹相间隔;l任一条进入d点的根轨迹与相邻的离开d点的根轨迹方向之间的夹角为;因此只要确定了d点附近的一条根轨迹的方向,由上述规律就可以方便地确定d点附近所有的根轨迹方向,而确定d点附近根轨迹方向的方法可根据法则2、法则4或取试验点用相角条件来验证。4210011001010101101000101001011九、根轨迹与虚轴的交点•如根轨迹与虚轴相交,则交点上的值和值可用劳思判据判定,也可令闭环特征方程中的,然后分别令其实部和虚部为零求得。Ksj4210011001010101101000101001011例4-7•设系统开环传递函数为试绘制闭环系统的概略根轨迹。2()()(3)(22)KGsHsssss4210011001010101101000101001011解解:按步骤画图①有4条根轨迹②各条根轨迹分别起于开环极点0,-3,-1+j1,-1-j1;终于无穷远③实轴上的根轨迹在0到-3之间④渐近线00(21)45,13540311111.254aakjj4210011001010101101000101001011⑤确定分离点d4110idp12,32.3,0.920.37ddj解方程得(舍去)421001100101010110100010100101131323434000000018018013526.579071.5671.56pppppppp⑥确定起始角4210011001010101101000101001011⑦确定根轨迹与虚轴的交点。2()(3)(22)0DsssssK1.095,8.16Ksj令代入上式解得闭环系统的特征方程为4210011001010101101000101001011图4-17例4-7根轨迹4210011001010101101000101001011十、根之和与根之积11112121()()()nmnijiijinnnnnspKszsssasasasa•如果系统特征方程写成如下形式①闭环特征根的负值之和,等于闭环特征方程第二项系数。若根之和与开环根轨迹增益无关。1a()2nmK4210011001010101101000101001011Tips在开环极点已确定不变的情况下,其和为常值,因此,n-m2的系统,当增益K的变动使某些闭环极点在s平面上向左移动时,则必有另一些极点向右移动,这样才能保证极点之和为常值。这对于判断根轨迹的走向很有意义。(1)n②闭环特征根之积乘以,等于闭环特征方程的常数项。4210011001010101101000101001011例4-82()(0.051)(0.050.21)KGsssss•已知单位负反馈系统开环传递函数为0KKK临试画出时的闭环系统的概略根轨迹,并求出时的闭环传递函数及闭环极点。4210011001010101101000101001011解;根据根轨迹绘制法则,按步计算:①n=4,有四条根轨迹;②起始于开环极点0,-20,-2-j4,-2+j4,终于无穷远处;③实轴上的根轨迹在(0,-20)区间;④n=4,m=0,则有4条根轨迹趋于无穷远,它们的渐近线与实轴的交点和夹角为421001100101010110100010100101120242464(21)(21)4aajjkknm4ii=1p=n-m取0,45;1,451,135;2,135aaaakkkk4210011001010101101000101001011⑤根轨迹的起始角。313234340000000180180116.512.5903939pppppppp解得⑥分离点坐标d。11110202424dddjdj12315.1,1.452.07,1.452.07ddjdj舍4210011001010101101000101001011⑦根轨迹与虚轴交点。2()(20)(420)4000DsssssK系统特征方程1230,4.1,4.1,3.47K临解得解得12s=j4.1,s=-j4.1则两个闭环极点sj令令代入代入4210011001010101101000101001011此时特征方程特征方程为2432()(20)(420)4000()241004001388.90DsssssKDsssss临344.2,19.8ss利用综合除法,可求出其他两个闭环极点4210011001010101101000101001011图4-19例4-8根轨迹图4210011001010101101000101001011图4-18常见闭环系统根轨迹图42100110010101011010001010010114-3广义根轨迹一、开环零点变化时的根轨迹()()GsHs设系统开环传递函数为()()10GsHs(4-59)闭环特征方程为()10()PsAQs(4-60)等效变换成返回子目录4210011001010101101000101001011令11()()()()PsGsHsAQs(4-61)显然,利用式4-61就可以画出关于零点变化的根轨迹,它就是广义根轨迹。42100110010101011010001010010111()()(2)()KGsHssssp二、开环极点变化时的根轨迹211132(2)()()2pssGsHsssK•设一负反馈系统的开环传递函数为10p现在研究变化的根轨迹。•等效开环传递函数为1p根据式(4-62)可画出变化时的广义根轨迹。4210011001010101101000101001011已知系统的开环传递函数为试绘制当开环增益K为时,时间常数变化时的根轨迹。例4-10()()(1)(1)aKGsHsssTs1,1,220aT解:题目显然是求广义根轨迹问题。4210011001010101101000101001011系统特征方程为()(1)(1)0aDsssTsK2112(1)()()aTssGsHsssK等效开环传递函数为等效开环传递函数有3个零点,即0,0,-1;2个极点,不同K值可计算出不同极点。按照常规根轨迹的绘制法则可绘制出广义根轨迹如图4-21。4210011001010101101000101001011图4-21例4-10根轨迹图4210011001010101101000101001011分析复杂控制系统如图,其中内回路为正反馈。为了分析整个控制系统的性能,需求出内回路的闭环零、极点。用根轨迹的方法绘制正反馈系统的根轨迹。三、零度根轨迹图4-2242100110010101011010001010010111DsGsHs特征方程1sHsG根轨迹方程研究内回路4210011001010101101000101001011从而相角方程及模值方程相应为kpszsniimii211111miiniiszKsp4210011001010101101000101001011使用常规根轨迹法绘制零度根轨迹时,对于与相角方程有关的某些法则要修改•实轴上某一区域,若其右方开环实数零、极点个数之和为偶数,则该区域必是根轨迹。•根轨迹的渐近线mnkA2a计算公式不变。4210011001010101101000101001011根轨迹的起始角与终止角nijjppmjpzpijijik112mjzpmijjzzzijijik112分离角与会合角除上述四个法则外,其他法则不变除上述四个法则外,其他法则不变4210011001010101101000101001011例4-11图4-23•正反馈系统的结构图如图4-23所示,0K试绘制开环系统根轨迹增益变化时的根轨迹。2(2)(),()1(3)(22)KsGsHssss其中4210011001010101101000101001011解:该系统是正反馈系统。0K当变化时的根轨迹是零度根轨迹。利用零度根轨迹法则绘制该系统的闭环根轨迹。12z终止于开环零点(3,)(2,)和•实轴根轨迹在区间内。起始于开环极点1233,11,11ppjpj4210011001010101101000101001011图4-24例4-11根轨迹图42100110010101011010001010010114-4系统闭环零、极点分布与阶跃响应的关系)()(sHsGK对某零点)(tr由开环→闭环极点的根轨迹求闭环极点确定闭环传函闭环系统动态性能主要任务:返回子目录4210011001010101101000101001011一、用闭环零、极点表示的阶跃响应表达式N阶系统的闭环传递函数可写为:niimjjnnnmmmsszsKasasabsbsbsRsCs11110110)()()()()(为闭环传递函数的零点jz为闭环传递函数的极点is4210011001010101101000101001011设输入为单位阶跃:r(t)=1(t),有:ssszsKsRssCniimjj1)()()()()(11假设(s)中无重极点,上式分解为部分分式nkkknnssAsAssAssAsAsC10110)(4210011001010101101000101001011)0()()(0110sniimjjsszsKAnkiiikkmjjkssnkiiimjjkssszsKssszsKAk1111)()()()(4210011001010101101000101001011将C(s)表达式进行拉式反变换得:nktskkeAtC1)0()((4-74)从上式看出,系统单位阶跃响应将由闭环极点及系数决定,而系数也与闭环零、极点分布有关。4210011001010101101000101001011二、闭环零、极点分布与阶跃响应的定性关系•稳定性所有闭环极点位于s平面的左半部;045•复数极点设置在s平面中与负实轴成夹角线附近;平稳性nktskkeAtC1)0()(4210011001010101101000101001011快速性闭环极点远离虚轴;动态过程尽快消失11()()mkjjknkkiiikKszAsssnktskkeAtC1)0()(小,闭环极点之间间距大,零点与极点间间距小。kA4210011001010101101000101001011三、主导极点和偶极子•主导极点:就是对动态过程影响占主导地位的极点,一般是离虚轴最近的极点。iiikkkjsjs如果有两个极点:的作用就可以忽略。,极点若ikis44210011001010101101000101001011•偶极子:就是一对靠得很近的闭环零、极点。就可以将其忽略不计。在对系统进行分析时,是一对偶极子。与时,就可以认为当ikkikzsszs1.04210011001010101101000101001011四、利用主导极点估算系统的性能指标•既然主导极点在动态过程中起主要作用,那么,计算性能指标时,在一定条件下就可以只考虑暂态分量中主导极点对应的分量,将高阶系统近似看做一、二阶系统,直接应用第三章中计算性能指标的公式和曲线。4210011001010101101000101001011例4-1221()(0.671)(0.010.081)ssss试近似计算系统的动态性能指标。%,st12,31.5,49.2ssj解:这是三阶系统,有三个闭环极点其零、极点分布如图4-25所示。•某系统的闭环传递函数为4210011001010101101000101001011极点离虚轴最近,所以系统的主导极点为,而其他两个极点可以忽略。1s1s图4-254210011001010101101000101001011这时系统可以看做是一阶系统。传递函数为式中:T=0.67s根据时域分析可知一阶系统无超调,调节时间11()0.6711ssTs%0330.672.01stTss4210011001010101101000101001011例4-13•系统闭环传递函数•试估计系统的性能指标。20.591()(0.671)(0.010.081)sssss4210011001010101101000101001011解:闭环零、极点分布如图(4-26)所示图4-264210011001010101101000101001011系统近似为二阶系统21()0.010.081sss10.4,10ns22/10.43.14/10.4%100%100%25%3.53.50.880.410seetss对应性能指标4210011001010101101000101001011例4-14•已知系统开环传递函数为•试应用根轨迹法分析系统的稳定性,并计算闭环主导极点具有阻尼比0.5时的性能指标。()(1)(0.51)KGssss4210011001010101101000101001011解:2()(1)(2)(1)(2)2KGssssKsssKK图4-27根轨迹图图4-27根轨迹图按步骤作出系统的根轨迹,如图4-27所示。4210011001010101101000101001011分析系统稳定性03K在平面上画出时的阻尼线。阻尼线与根轨迹交点的坐标设为,从图上测得,与之共轭的复数极点为。10.330.58sj20.330.58sj0.51s32.34s已知系统闭环特征方程及两个极点,用长除法求出第三个极点。•使系统稳定的开环增益范围是4210011001010101101000101001011系统闭环传递函数近似为二阶系统二阶系统在单位阶跃信号作用下的性能指标:20.445()0.6670.445sss22/10.53.14/10.5%100%100%16.3%3.53.510.50.50.667sneetss42100110010101011010001010010114-5系统阶跃响应的根轨迹分析•例4-15已知系统结构如图4-28所示。试画出当由时的闭环根轨迹,并分析对系统动态过程的影响。K0K图4-28返回子目录4210011001010101101000101001011解:•系统开环传递函数有两个极点0,-2;有一个零点-4。•此类带零点的二阶系统的根轨迹,其复数部分为一个圆,其圆心在开环零点处,半径为零点到分离点的距离。•根轨迹如图4-29所示。4210011001010101101000101001011图4-294210011001010101101000101001011系统根轨迹分离点121.172,6.83dd1111112221.1720.8280.34342.82820.68611.7,23.4ddKdKKKK•对应开环增益1.当开环增益在(0~0.686)内,闭环为两个负实数极点,系统在阶跃信号下响应为非周期的。2.当开环增益在(0.686~23.4)内,闭环为一对共轭复数极点,其阶跃响应为振荡衰减过程。4210011001010101101000101001011下面求系统最小阻尼比对应的闭环极点。过原点做与根轨迹圆相切的直线,此切线与负实轴夹角的余弦即为系统的阻尼比。(23.4~)3.当开环增益在内,闭环又为负实数极点,其阶跃响应又为非周期的。42100110010101011010001010010110coscos450.7071,222sj对应闭环极点系统阶跃响应具有较好的平稳性。4210011001010101101000101001011例4-162()(10)KGsss单位反馈系统的开环传递函数试绘出闭环系统的根轨迹。4210011001010101101000101001011解:此系统开环有三个极点0,0,-100KKjKa10360601p2p3p图4-30按步骤作出系统的根轨迹,如图4-30所示。4210011001010101101000101001011图中两条根轨迹位于s平面右半部,即闭环始终有两个右极点。说明开环增益无论取何值,系统均不稳定。1210KszGsss()()()10~10431z将设置在()之间,则附加零点后的系统根轨迹如图所示。若在系统中附加一个负实数零点z1,用来改善系统的动态性能,则系上统的开环传递函数为4210011001010101101000101001011j1p2p3p0K102zK090900K图4-31附加零点后的根轨迹4210011001010101101000101001011明显看出,当开环增益K由0时,系统根轨迹全部位于s平面左半部,即K取何值系统均稳定。当0>g=tf(1,[2,1]);>>bode(g)>>nyquist(g);返回子目录5-3系统的开环频率特性•一、开环幅相特性曲线•设系统开环传递函数由若干典型环节串联123GsGsGsGs313(())1()iijGjiiGjGje开环频率特性系统开环幅频与相频分别为31()iiAGjGj123331120lg()20lg()20lg()iiiiLGjGjGj1、开环幅相特性曲线(1)当niisTKsG11系统开环传递函数不包含积分环节和微分环节图5-20系统开环幅相特性曲线时,20j0j001jTKjG,1n1-=时,当=时,当若GKG22j0j001j1jTKjG,2n21-=时,当=时,当+若GKGT(2)当niimiisTsKsG1111图5-21取m=1,n=3时系统开环幅系统开环传递函数分子有一阶微分环节,其开环幅相特性曲线出现凹凸时,2n-m02n2m0j0j00nm2202320j0j0011j1T1KG1s1s1T1sKG,3,1m32113211=时,当=时,当个惯性环节:个一阶微分环节和当有=时,当=时,当++++++若GKGGKGjTTjjjTTssn(3)当1TssKsG图5-22含有积分环节时的开环幅相特性曲线开环传递函数有积分环节时,频率趋于零时,幅值趋于无穷大。时,230j22j001TjKG1TsKG,2220j2j001TjKG1TsKG,122-=时,当-=时,当若-=时,当-=时,当若GGjjssGGjjss2.系统开环幅相的特点①当频率ω→0时,其开环幅相特性完全由比例环节和积分环节决定。②当频率ω→∞时,若n>m,G(jω)=0相角为(m-n)π/2。③若G(s)中分子含有s因子环节,其G(jω)曲线随ω变化时发生弯曲。④G(jω)曲线与负实轴的交点,是一个关键点。已知单位反馈系统的开环传递函数为)1)(15.0()21()(2ssssksGk试概略绘出系统开环幅相曲线。2v180)0(jGk2700)(jGk)]5.0()5.21([1)25.01()(22222jkjGk解系统型别(2)终点(3)与坐标轴的交点,零点—极点分布图如图5-22(a)所示。显然(1)起点二、开环对数频率特性曲线的绘制4321系统开环对数幅频等于各环节的对数幅频之和,相频等于各环节相频之和。系统开环对数幅频与对数相频表达式为系统开环对数幅频与对数相频表达式为441120lg()20lg()20lg()iiiiLGjGjGj例5-1•绘制系统开环对数幅频与相频特性曲线。)1)(11.0(10)(sssG解:1111.0110)1)(11.0(10)(sssssG系统开环传递函数100.110.1arctan10.1lg2010.112)G111arctan1lg20112)G02010lg20lg20101)G3323322222111惯性环节的转折频率惯性环节的转折频率LssLssdBjGLs开环由三个典型环节组成,每个环节的对数幅频与相频特性均是已知的。将各环节的对数幅频与相频曲线绘出后,分别相加即得系统的开环对数幅频及相频。例5-2)15.0(105.0111110)20)(1()2(100)(sssssssssG(0.51)s51011s211s310.051s4五个基本环节s/rad1T1arctan1lg2011)32lg201lg201)202010lg20lg2010)13332332221111转折频率LsGLssGdBALsGs/rad20.51T10.5arctan10.5lg2010.5s5s/rad200.051T10.05arctan10.05lg2010.051)4554255444244转折频率)转折频率LGLsG绘制开环系统的波特图–将写成典型环节之积;–找出各环节的转角频率;–画出各环节的渐近线;–在转角频率处修正渐近线得各环节曲线;–将各环节曲线相加即得波特图。一般规则:例5-3)12.0(121110)12()12.0(10)(sssssssGs/rad50.21T110.2lg2010.2s)4s/rad5.0T112lg20121)3lg201lg201)22010lg20lg2010)1442543323322111转折频率转折频率LGLsGLssGdBALsG例5-4已知最小相位系统的开环对数幅频渐进特性曲线,求系统的开环传递函数。111121sssKsG12c1ccK0dB120lg20lg20lgK0dBKc等于数幅频渐进特性叠加后时,三个环节叠加的对当来求:可用已知的截止频率开环增益5-4频率稳定判据一、奈奎斯特稳定判据图5-17反馈控制系统sNsMsG11sNsMsH22返回子目录开环传递函数sNsNsMsMsHsG2121闭环传递函数121212()()()()1()()()()()()MsNsGssGsHsNsNsMsMssNsNsMsMsNsNsHsGsF2121211令将F(s)写成零、极点形式,则niiniipszssF11辅助函数F(s)具有如下特点:①其零点和极点分别是闭环和开环的特征根。②其零点的个数与极点的个数相同。③辅助函数与系统开环传递函数只差常数1。)(sFFj1z2ziz1iz1pizssABjsFniiniipszssF112sF由niiniipszssF111.幅角原理1.幅角原理•如果封闭曲线内有Z个F(s)的零点,有P个F(s)的极点,则s依顺时针转一圈时,在F(s)平面上,F(s)曲线绕原点反时针转的圈数R为P和Z之差,即R=P-Zss•若R为负,表示F(s)曲线绕原点顺时针转过的圈数。s平面s映射F(s)正虚轴j(:0)F(j)(:0)负虚轴j(:0)F(j)(:0)半径的半圆2.奈式判据图5-29包括全部右半平面地封闭曲线平面。s)就包含了整个右半为奈奎斯特路(段组组成的封闭曲3这样,。0变化到-由:js负虚轴iii;2/-变化到2/由R,:Res为无限大的右半圆半ii;变到0由:js正虚轴i段3由以下曲线平面。设面s扩展为整个右半闭曲线点数,平面内的所有零点、极位于右半为了确定辅助函数j径称频率,半圆径频率组成现将2.奈式判据F(j)和G(j)H(j)只相差常数1。F(j)包围原点就是G(j)H(j)包围(-1,j0)点。GH平面0F平面1对于G(j)H(j):0,开环极坐标图;:0,与开环极坐标图以轴镜像对称;F平面(1,j0)点就是GH平面的坐标原点。奈氏判据:已知开环系统特征方程式在s右半平面根的个数为P,开环奈氏曲线(:0)包围(1,j0)点的圈数为R,则闭环系统特征方程式在s右半平面根的个数为Z,且有Z=PR若Z=0,闭环系统是稳定的。若Z0,闭环系统是不稳定的。或当开环系统稳定时,开环奈氏曲线不包围(1,j0)点时,则闭环系统是稳定的。当开环系统不稳定时,开环奈氏曲线包围(1,j0)点P圈时,闭环系统是稳定的。2.奈式判据)()(0sGsksGvk0+开环有积分环节的系统由于开环极点因子1/s,既不在的s左半平面,也不在的s右半平面,开环系统临界稳定。在这种情况下,不能直接应用奈氏判据。j0如果要应用奈氏判据,可把零根视为稳定根。因此,在数学上作如下处理:在平面上的s=0邻域作一半径无穷小的半圆,绕过原点。02.奈式判据)()(0sGsksGvk0js+0js+abc0js0jsabc002,,2,0:0,,0,0:2,,2,0:sHsGcsHsGbsHsGaeKeKsHsGjj在GH平面上开环极坐标图在=0时,小半圆映射到GH平面上是一个半径为无穷大,从=0到=0+顺时针旋转v•180°的大圆弧。如此处理之后,就可以根据奈氏判据来判断系统的稳定性了。ImRe0=0+增补线=0-用奈氏判据判断系统稳定性时,一般只须绘制从0时的开环幅相曲线,然后按其包围(-1,j0)点的圈数N(逆时针为正,顺时针为负)和开环传递函数在s右半平面根的个数P,根据公式Z=P2N来确定闭环特征方程正实部根的个数,如果Z=0,闭环系统是稳定的。否则,闭环系统是不稳定的。如果开环传递函数包含积分环节,且假定个数为N,则绘制开环极坐标图后,应从=0+对应的点开始,补作一个半径为,逆时针方向旋转v90的大圆弧增补线,把它视为奈氏曲线的一部分。然后再利用奈氏判据来判断系统的稳定性。2.奈式判据(实际方法)例5-5•已知系统开环传递函数试应用奈氏判据判别闭环系统稳定性。5211000)(ssssG2.0arctan5.0arctanarctan22212.015.01100jG12.015.01100sG)1jesss曲线画出系统开环幅相特性定。点,所以闭环系统不稳,幅相曲线包围即开环系统稳定,开环,,可确定由开环传递函数系统稳定性根据奈氏判据判别闭环j010PsG)2Z=P-2N=0-2(-1)=2,不稳定例5-6•已知系统开环传递函数试应用奈氏判据判别K=0.5和K=2时的闭环系统稳定性。1)(sKsG1)分别作出K=0.5和K=2时开环幅相特性曲线2)根据开环传递函数,P=1。•K=0.5时,绕(-1,j0)点转过的圈数为0,Z=P-2N=1,闭环系统不稳定。•K=2时,绕(-1,j0)点反时针转过圈数为1/2,Z=P-2N=1-2(1/2)=0,闭环系统稳定。图5-32系统开环幅相特性曲线例5-7•已知系统开环传递函数试应用奈氏判据闭环系统稳定性。1)(2TssKsG曲线画出系统开环幅相特性)1的半圆。半径为向反时针方向补画一个的点开始在开环幅相特性曲线上有两个积分环节,需要开环传递函数0sG)2。的个数闭环特征方程正实部根定。点,所以闭环系统不稳,曲线包围了,而开环开环正极点数21202NPZj01jG0P)3ReIm01(+)()由图可知,幅相曲线不包围(1,j0)点。此结果也可以根据增加时幅相曲线自下向上(幅角减小)和自上向下(幅角增加)穿越实轴区间(,1)的次数决定。N=NN自实轴区间(,1)开始向下的穿越称为半次正穿越,自实轴区间(,1)开始向上的穿越为半次负穿越。二、对数频率稳定判据奈氏判据也可叙述为:在开环幅相特性曲线,沿增加的方向,对(-1,)的负实轴段正、负穿越次数之差等于,则闭环系统稳定。/2P/2NNPjHjG二、对数频率稳定判据•若开环系统稳定(p=0),则闭环系统稳定的充要条件是:在的所有频段内,正负穿越线的次数差为0。dBL0)()(180注意:在开环对数幅频特性大于零的频段内,相频特性曲线由下(上)往上(下)穿过负1800线为正(负)穿越。N+(N-)为正(负)穿越次数,从负1800线开始往上(下)称为半个正(负)穿越。图5-34幅相曲线(a)及对应的对数频率特性曲线(b)系统闭环稳定的条件是:在开环对数幅频的频段内,对应的开环对数相频特性曲线对线的正、负穿越次数之差为。即为系统开环传递函数位于右半平面的极点数。20lg()0Gj/2P/2NNPPs当开环系统有积分环节时,对应在对数相频曲线上处,用虚线向上补画,在计算正负穿越将补画的虚线看成对数相频曲线的一部分。02例5-8•已知系统开环传递函数试用对数判据判别闭环稳定性。)11.0(10)()(sssHsG解:绘制系统开环对数频率特性如图。由开环传递函数可知P=0。图5-35所以闭环稳定002NNNP例5-10•已知系统开环传递函数•试用对数判据判别闭环稳定性。)1002(300)()(2ssssHsG解:绘制系统开环对数频率特性如图•图5-37•在处振荡环节的对数幅频值为n120lg20lg20.1142dB闭环不稳定。202(1)2ZPN•闭环特征方程的正根数为c)(jGg曲线与负实轴交点处的频率称为相角交界频率曲线与单位圆交点处的频率称为截止频率)(jG三、稳定裕度——衡量闭环系统稳定程度的指标。三、稳定裕度——衡量闭环系统稳定程度的指标。相位裕度极坐标图1)()(jHjG的矢量与负实轴的夹角。0lg20GH)(即对数坐标图上处与的差)(180)180()(cc模稳定裕度h:)(gA幅值裕度是指(-1,j0)点的幅值1与之比,用h表示)(1gAh在对数坐标图上20lg20lg()()gghAL)(gL即h的分贝值等于与0dB之间的距离(0dB下为正)2h40dBh6lg20c相角裕度的物理意义在于:稳定系统在截止频率处若相角再迟后一个角度,则系统处于临界状态;若相角迟后大于,系统将变成不稳定。hg)(gAh幅值裕度的物理意义在于:稳定系统的开环增益再增大倍,则处的幅值等于1,曲线正好通过(-1,j0),点系统处于临界稳定状态;若开环增益增大倍以上,系统将变成不稳定。一般要求:)5)(1()(0sssKsG100K例5-11某单位反馈系统的开环传递函数为试求时系统的相角裕度和幅值裕度。解15)151)(1(5)(00KKsssKsG250KK)(L绘制开环增益时的曲线当2K时)20(21211)5(12)(2222222ccccccccA2c5.198.157.54905arctanarctan90180)(1801cccjG0)5arctan(arctan90180)(180gggjGarctanarctan(5)90ogg90tan5152ggg0512g236.25gdBAhgggg9.8793.221)5(1)(1221得,即。5-5系统闭环频率特性与阶跃响应的关系•图示单位反馈系统的闭环传递函数为()()1()GssGs()()1()GjjGj图5-40返回子目录)1)(1()(21sTsTsKsGPAOAPAOAj)(PAOAM)(PAOA)()()()(1)()(jeMjGjGjOAjG)(PAjG)(1)()(jM)()(jp22222211MMYMMXjYXjG)(PAOA)(等M圆—为常数的轨迹设)()()(MjjYXjYXGGM11)(整理得—等圆方程M)()1(2222MYXYX一、等M圆图和等N圆图•根据开环幅相曲线,应用等M圆图,可以作出闭环幅频特性曲线,应用等N圆图,可以作出闭环相频特性曲线。OAPjYXjG)(设jYXjYXGGj11)(2222412121NNNYX整理得—等圆方程N2222)1(YXjYYXX22arctan)(YXXY22)(tanYXXYN等N圆—为常数的轨迹一、等M圆图和等N圆图二、尼科尔斯图(N.b.Nichols)•如果将开环频率特性表示为jeAjGjjjeAeAeM1•则sin20lg20lgsinA11coscoslg20lg20222MMA做变换得由等M线和等线组成的图,称为尼科尔斯图。如图5-45所示。图5-45尼科尔斯图三、利用闭环幅频特性分析和估算系统的性能在已知闭环系统稳定的条件下,可以只根据系统闭环幅频特性曲线,对系统的动态响应过程进行定性分析和定量估算。图5-48闭环幅频特性曲线定性分析(0)M1)零频的幅值反映系统在阶跃信号作用下是否存在静差。;态误差,,在阶跃信号下没有静当;态误差,,在阶跃信号下没有静当0e10M0e10Mssss2)谐振峰值反映系统的平稳性。此值大说明动态过程超调量大,平稳性差,反之平稳性好。mM平稳性差小有峰值,二阶系统:有峰值,一阶系统:幅频曲线没%M,121M0%m2m3)带宽频率反映系统的快速性b下降到0.707对应的频率值)(M0Mb11)(TssTb1bcsTt333一阶系统:快速性越好,sbt707.0)2()()(22222bnbnnbM42244221nb422442215.3sbt2222)(nnnsss二阶系统221nr2121rM)707.00(nst5.3快速性越好,sbtb()M4)闭环幅频在处的斜率反映系统抗高频干扰的能力。斜率越陡,抗高频干扰的能力越强。定量估算5.05.005.0201151.257.13%174ln41%MMtMMMbmsbm用频域分析方法估算系统的动态性能st00)(jG)(j实验测试稳定性稳定裕度0MrrM,bchg闭环频率特征量奈氏判据对数判据)(jGi总结§5-6开环频率特性与系统阶跃响应的关系图5-51系统开环对数幅频渐近特性曲线返回子目录•低频段通常是指的渐近曲线在第一个转折频率以前的区段,这一段的特性完全由积分环节和开环增益决定。一、低频段20lg()Gj)(LK低频段渐近线集中反映了系统跟踪控制信号的稳态精度信息。根据低频段可以确定系统型别和开环增益,利用第3章中介绍的静态误差系数法可以确定系统在给定输入下的稳态误差。二、中频段•中频段特性集中反映了系统的平稳性和快速性。图5-53二、中频段•中频段特性集中反映了系统的平稳性和快速性。ssKsGc11111ssssGsGscccsccst,/3t,系统具有较好的平稳性高一些斜率线,配置较宽的c20dB/dec二、中频段•中频段特性集中反映了系统的平稳性和快速性。22c2ssKsG2c22c22c22c11ssssGsGs程持续振荡系统临界稳定,动态过,0显著增大。,斜率线不宜过宽,否则中频段st%40dB/dec三、高频段对于单位反馈系统)(1)()(jGjGj0)(lg20jG1)(jG在高频段,一般有,即)()(1)()(jGjGjGj系统开环对数幅频在高频段的幅值,直接反映了系统对输入高频干扰信号的抑制能力。高频特性的分贝值越低,系统抗干扰能力越强。三个频段的划分并没有严格的确定准则,但是三频段的概念,为直接运用开环特性判别稳定的闭环系统的动态性能指出了原则和方向。重点掌握①频率特性的定义及系统在正弦信号作用下的稳态输出。②绘制频率特性图(Nyquist图和Bode图)。③根据Bode图求传递函数。本章知识点及主要线索部件闭环系统稳定性开环,h()20lg()()GjGjGj对数判据,p乃氏判据,p()M,,,,cKhb0rω,M,M尼科尔斯图三频段定性闭环幅频特性00,ssste解.依题意,当时要求(rad/s)π10π259.0111122TjT0154.019.011π102T即2229.011T例4一台笔录仪的传递函数为,要求在5Hz以内时,记录仪的振幅误差不大于被测信号的10%,试确定记录仪应有的带宽11)(Tss?b(rad/s)833.640154.011Tb第六章控制系统的校正第6章控制系统的校正基本要求6-1系统校正设计基础6-2串联校正6-3串联校正的理论设计方法6-4反馈校正6-5复合校正返回主目录基本要求①正确理解串联超前、串联滞后、串联滞后-超前三种校正的特性及对系统的影响。②掌握基本的校正网络及运算电路。③熟练掌握运用(低、中、高)三频段概念对系统校正前、后性能进行定性分析、比较的方法。④熟练掌握串联校正(串联超前、串联滞后)的频率域设计步骤和方法。了解串联校正的根轨迹设计步骤和方法。返回子目录⑤正确理解反馈校正的特点和作用。能通过传递函数分解为典型环节的方法,比较说明加入反馈局部校正的作用。⑥正确理解对控制作用和对干扰作用的两种附加前置校正的特点、使用条件及其作用,会使用等效系统开环频率特性分析或闭环零、极点比较分析来说明前置校正的作用。⑦了解其它一些改善系统性能的手段与方法。6-1系统校正设计基础时域:一、性能指标strt调节时间上升时间无差度稳态误差和开环增益等。超调量σ%返回子目录常用频域指标:模稳定裕度:GM峰值:pM峰值频率:r带宽:B相稳定裕度:pm截止频率:c复数域指标是以系统的闭环极点在复平面上的分布区域来定义的。•图6-1闭环极点的限制区域振荡度:φ衰减度:η二、几种校正方式•图6-2三、校正设计的方法1.频率法2.根轨迹法3.等效结构与等效传递函数方法由于前几章中已经比较详细地研究了单位负反馈系统和典型一、二阶系统的性能指标,这种方法充分运用这些结果,将给定结构等效为已知的典型结构进行对比分析,这样往往使问题变得简单。6-2串联校正•图6-4系统的串联校正返回子目录一、相位超前校正•由图6—5可见,校正作用的主要特点是提供正的相移,故称相位超前校正图6-5相位超前校正装置的传递函数aTm111sin1aam超前角的最大值为这一最大值发生在对数频率特性曲线的几何中心处,对应的角频率为111)(aTsaTssGc(6-1)例6-1图6-6•单位负反馈系统原来的开环渐近幅频特性曲线和相频特性曲线如图6-6所示,它可以看作是根据给定稳定精度的要求,而选取的放大系数K所绘制的。从以上的例子可以看出超前校正,可以用在既要提高快速性,又要改善振荡性的情况。图6-7无源微分网络通常式(6—1)的传递函数可以通过图6—7所示的无源网络来实现。利用复数阻抗的方法不难求出图6—7所示网络的传递函数为1111)(aTsaTsasGc221RRRaCRRRRT2121二、滞后校正1()1cbTsGsTs(1)b滞后校正传递函数为例6-2•单位负反馈系统原有的开环Bode图如图6—9中曲线所示。•曲线可以看作是根据稳态精度的要求,所确定的开环放大系数而绘制。1L系统动态响应的平稳性很差或不稳定,对照相频曲线可知,系统接近于临界情况。图6-9例6-2对应的波特图注意:由于校正环节的相位滞后主要发生在低频段,故对中频段的相频特性曲线几乎无影响。因此校正的作用是利用了网络的高频衰减特性,减小系统的截止频率,从而使稳定裕度增大,保证了稳定性和振荡性的改善,因此可以认为,滞后校正是以牺牲快速性来换取稳定性和改善振荡性的。例6—3•设单位负反馈系统未校正时的对数频率特性如图6—10中曲线所示,校正网络对应的幅频特性如图中曲线所示。•由图可见,并未改变低频段的斜率与高度,这说明稳态精度并未由于滞后校正而直接改善。•通过提供了通过增加开环放大系数,提高低频区幅频特性高度的可能性。图6-10例6-3对应的波特图通常式(6-5)的传递函数可以通过图6-11所示的无源网络来实现212()1()()()1ccrUsRCsGsUsRRCs三、滞后-超前校正•为了全面提高系统的动态品质,使稳态精度、快速性和振荡性均有所改善,可同时采用滞后与超前的校正,并配合增益的合理调整。•鉴于超前校正的转折频率应选在系统中频段,而滞后校正的转折频率应选在系统的低频段,因此可知滞后—超前串联校正的传递函数的一般形式应为121,1abbTaT1212(1)(1)()(1)(1)cbTsaTsGsTsTs(6-7)式(6-7)的传递函数可用如图6-12所示的无源网络来实现。图6-12图6—12所示的无源网络,它的传递函数为11CRTa22CRTbabTT1a)1)(1()1)(1()(1saTsTasTsTsGbabac(6-10)式(6-10)中前一部分为相位超前校正,后一部分为相位滞后校正。对应的波特图如图6-13所示。由图看出不同频段内呈现的滞后、超前作用。图6-13式(6-10)对应的波特图四、PID校正器1.PD校正器又称比例-微分校正,其传递函数()()(1)(1)cdpdcpppGsKsKKGsKKTsK(6-11)作用相当于式(6-1)的超前校正。2PI校正器PI校正器又称比例-积分校正,其传递函数111()ipcpiiTKsGsKTsTs(6-12)作用相当于式(6-5)的滞后校正。又称比例—积分—微分校正,其传递函数其作用相应于式(6—7)的滞后—超前校正。3PID校正器21()1cpdiidipiGsKKsTsTKsTKsTs(6-13)注意:•校正装置参数的合理选择和系统开环增益的配合调整是非常重要的。•例如,若将超前校正环节的参数设置在系统的低频区,就起不到提高稳定裕度的作用。同理若将滞后校正环节的参数设置在中频区,会使系统振荡性增加甚至使系统不稳定。6-3串联校正的理论设计方法一、串联校正的频率域方法•频率域设计的基础是开环对数频率特性曲线与闭环系统品质的关系。•在应用时首先需要把对闭环系统提出的性能指标,通过转换关系式,近似地用开环频域指标来表示。返回子目录例6-4•给定系统结构图如图6—14所示。设计和K,使得系统在r(t)=t作用下稳态误差≤0.01相稳定裕度≥,截止频率)(sGcsradc/4045解:100K,10001.01取KKersssradc/311)根据稳态误差的要求调整K2)根据K=100,作出未校正的开环对数幅频特性和相频特性0010180(903.1)17.9tg解:sradc/44'6log10a441aT4a01136.0T3)选取相位超前校正371414arcsin,101136.0104544.0mcsssG校正后开环传递函数为)11.0)(101136.0()104544.0(100)()(sssssGsGc校正后相稳定裕度为符合要49.8图6-15系统的串联超前校正•串联超前校正方法2.doc串连校正方法2二、串联校正的根轨迹方法•根轨迹设计的基础是闭环零、极点与系统品质之间的关系。•闭环的品质通常是通过闭环主导极点来反映的。•因此在设计开始,需要把对闭环性能指标的要求,通过转换关系式,近似地用闭环主导极点在复平面上的位置来表示。例6-5•设系统的结构图如图6-17所示要求设计串联超前校正环节,使得系统阶跃响应满足以下要求,超调量调节时间2sts0.16图6-17解:•图6-18主导极点的选取030BZOBPO1()110.3510.189aTsGsTsss•校正后系统开环传递函数为()()5.02(0.351)(0.51)(0.1891)cGsGsssss图6-19校正后系统的根轨迹例6-6•系统结构图如图6-20所示。•要求设计滞后校正和调整开环增益,使系统在作用下的稳态误差,并且阶跃响应的超调量。()rtt0.25rsse%20%图6-20例6-6的系统结构图解:•作出未加校正时系统的根轨迹,如图6-21所示。根据超调量要求选取系统阻尼比0.5。由原点做的阻尼线,与根轨迹交于B点。图6-21未加校正时系统的根轨迹600.750.753jB点在复平面上的位置14.6BKBOBCBDB点处的根轨迹增益为1.2212BKK故B点对应的K值为②确定滞后校正环节的参数b、T。如图6-22所示,在E点右侧取一点作为滞后环节零点的位置。10.2bT(6-19)1rsseK0.25rsse①根据系统稳态要求选取开环增益。要满足,K应取大于4的值。图6-221.220.244,520.49bT校正环节的传递函数为图6-22选取滞后校正的零点4.9981()20.491csGss③作出校正后的根轨迹图。图6-23()()5(4.9981)(20.491)(0.51)(0.1671)14.6(0.2)(2)(6)(0.0488)cGsGsssssssssss图中虚线框部分为原点附近的根轨迹。由图可知,校正后系统满足指标要求。返回子目录6-4反馈校正222()()1()()GsGsGsHs显然,引进H(s)的作用是希望的特性使整个闭环系统的品质得到改善。2()Gs反馈校正的几种作用①利用反馈改变局部结构、参数②利用反馈削弱非线性因素的影响③反馈可提高对模型扰动的不灵敏性④利用反馈可以抑制干扰一、利用反馈改变局部结构、参数①用位置反馈包围积分环节。'2(),()111(),(1)fffKGsHsKsGsTKTsKK使系统的无差度下降,相位滞后减少。②用速度反馈包围惯性、积分和放大环节。2'12111(),()(1)();,(1)11tttKGsHsKssTsKTKGsTKsTsKKKK可以增加系统的带宽,有利于快速性的提高。③用速度反馈包围一个小阻尼的二阶振荡环节和放大环节。22222'222(),(1)2()()2(0.5)nntntnnnKGsssHsKsKGssKKs加入速度反馈,增加了阻尼,减弱了小阻尼环节的不利影响。④速度反馈信号再经过一个微分网络22122122'12212122112112'"'"1'"'"121212(),()(1)11(1)()[()1](1)(1)(1)(1)(1)(1)(1)(1),ttttKTsKTsGsHsKssTsTsTsKTsGssTTsTTTKKsKTsKTsTssTsTssTsTsTsTTTTKKTTTTT可以保持增益不变,无差度不变;同时提高稳定裕度、抑制噪声、增宽频带。二、利用反馈削弱非线性因素的影响•最典型的例子是高增益的运算放大器。()()1GjHj(6-21)若满足'()()1()()GjGjGjHj由()()()jjGj’这表明G主要取决于H,而和无关若反馈元件的线性度比较好,特性比较稳定,那么反馈结构的线性度也好,特性也比较稳定,正向回路中非线性因素、元件参数不稳定等不利因素均可以削弱。'()1()()()()GjGjGjHjHj(6-22)三、反馈可提高对模型摄动的不灵敏性•摄动是由于模型参数变化或某些不确定因素引起的。•采取反馈校正比串联校正对模型的摄动更为不敏感。图6-25串联校正与反馈校正四、利用反馈抑制干扰图6-26利用反馈抑制干扰111GHGH只要,干扰的影响就可以得到抑制。从抑制测量噪声的角度,要求高频区。6-5复合校正•对于稳态精度、平稳性和快速性要求都很高的系统,或者受到经常作用的强干扰的系统,除了在主反馈回路内部进行串联校正或局部反馈校正之外,往往还同时采取设置在回路之外的前置校正或干扰补偿校正,这种开式、闭式相结合的校正,称为复合校正。具有复合校正的控制系统称为复合控制系统。返回子目录一、对控制作用的附加前置校正图6-27前置校正11pCsRsGsGsGs系统闭环传递函数令0sCsRsE011sRsGsGsGsCsRsEpsGsGp1101110(),()mmnnnbsbsbNsGsDssasasanm21210cGsdsdsd希望系统输出完全复现控制输入,即•根据误差定义,可以求出误差传递函数000011220111basbasbsbdsdsdasasassRsEmmmnmmnnn000bda)(10011bdbda)(0211202bdbdbda系统的无差度反映了系统在时间幂函数输入下的复现能力。结论•在系统设计中采用这种附加前置校正,对解决系统稳定性与稳态精度的矛盾、振荡性与快速性的矛盾,有着特殊可取之处。•因此精度要求高的快速随动系统,经常采用前置校正。采用附加前置校正的办法,实质上是将稳定性和稳态误差的要求分别来考虑。例6-7•系统如图6-28所示图中是附加的前置校正。系统在等速输入作用下无稳态误差,相当于无差度为2,而系统的闭合回路内仍只有一个积分环节。将图6-28所示系统化为图6-29所示的等效单位负反馈的典型形式。/0.855s图6-28025.7(1.171)()(0.0331)sGsss等效单位负反馈系统开环传递函数图6-29等效系统00(1)()()11cGGGCsRsGG等效传递函数二、对干扰的附加补偿校正•对于扰的补偿控制也是一种前置校正方式。•作用有干扰的系统结构图如图6—30所示图6-30干扰的前置补偿2112(1)()()1cGGGCsNsGG输出•单纯依靠回路的设计来达到干扰抑制,有一定的困难与不便。•利用附加的干扰补偿装置,实现干扰对系统输出的不变性,是一种非常有效的方法。11()()cGsGs(6-34)例6-8•假定原来的闭合回路的特征多项式已满足稳定条件,现要求设计,对干扰N进行补偿。()cGs图6-31•对干扰进行补偿的系统结构图如图6-31所示。解:111()(1)cGsTsK210121210(1)(1)limSSNsKTsessTsTsKKs根据式(6-34)对干扰N完全补偿的条件可得干扰所引起的稳态误差为零。若假定干扰为阶跃作用,只要取就可以达到稳态补偿。例6-9•系统如图6—32所示,图中干扰N不可测量,但系统中的a点或b点可测,试选择干扰补偿方案。图6-32解:•因为a点可测量,可将a点的变量看作干扰信号,组成干扰补偿通道,如图中虚线部分所示,这时全补偿的条件为14()()()0cGsGsGs41()()()cGsGsGs由此可得补偿器的传递函数另一种干扰抑制方案图6-33211321232123()1()()()1()1()GGWWCsRsNsGGWWGGWW(6—37)1212()()1GGCsRsGG则有这说明当没有干扰时,式(6-39)的关系可以保持输入与输出的关系不变,即式(6-37)中N=0时的关系。这时附加部分的输出相抵消,图6-33中的信号X=0若取121212()0,11NsGGWWGG3()Ws•该方案的实质是间接地检测出了干扰,再通过进行调整,从而使实际输出跟踪理想模型的输出。•上面所阐明的干扰抑制方案,可用在既要求保持输入输出关系不变又希望抑制不可量测干扰的情况。串联校正的根轨迹法和频率域法思路期望连接开环:sse抗干扰,st%,K开环低频段中频段高频段()L()cGscL0()Gs主导极点的根轨迹方程0()Gs补偿角校验,ccpzc1,2s,c第八章采样系统理论第8章采样系统理论8-1采样过程与采样定理基本要求8-2信号的恢复与零阶保持器8-3z变换与z反变换8-4脉冲传递函数8-5采样系统的性能分析8-6采样系统的数字校正返回主目录基本要求①正确理解采样过程,采样定理,信号复观和零阶保持器的作用,了解采样系统与连续系统的区别与联系。②Z变换和Z反变换,熟练掌握几种典型信号的Z变换和通过部分分式分解进行反变换,了解用Z变换法解差分方程的主要步骤和方法。③正确理解脉冲传递函数的概念,熟练掌握简单采样系统开环脉冲传递函数和闭环脉冲传递函数的计算方法,掌握典型闭环采样系统输出的Z变换表达式。返回子目录④熟练掌握Z域稳定性的判别方法。⑤熟练掌握采样瞬时的稳态误差的计算方法,正确理解终值定理的使用条件、积分环节与系统的型别的关系。⑥熟练掌握瞬态响应与极点分布的对应关系。⑦掌握最小拍采样系统的设计步骤。图8-1机载火力控制系统原理图8-1采样过程与采样定理一、采样过程——将连续信号转换成离散信号的过程1该过程可以看成是一个信号的调制过程,如图8-3所示,其中载波信号)(tp是一个周期为T,宽度为),的脉冲序列,如图8-3(b)所示。幅值为幅值正比于采样瞬时值的脉冲序列,如图8-3(c)所示。调制后得到的采样信号是一个周期为T,宽度为返回子目录T(图8-3信号的采样过程实现上述采样过程的装置称为采样开关可用图8-3(d)所示的符号表示。)()()(tftptf(8-1)由于载波信号)(tp是周期函数,故可以展成如下Fourier级数ntjnnseCtp)((8-2)则采样信号可以表示为)(tfntjnnsetfCtf)()((8-4)2/02/)2/sin(1)(1ssnssTtjnnennTdtetpTC(8-3)snC其中,为采样频率,Fourier系数由下式给出若连续信号的Fourier变换为,则采样信号的Fourier变换为)(jF连续信号与离散信号的频谱曲线如图8-4所示。)(tf)(tfnsnjnjFCjF)()((8-5)图8-4香农(Shannon)采样定理若存在一个理想的低通滤波器,其频率特性如图8-5所示,便可以将采样信号完全恢复成原连续信号。由此可得如下著名的:图8-5)香农(Shannon)采样定理如果采样频率满足以下条件smax2s式中为连续信号频谱的上限频率max则经采样得到的脉冲序列可以无失真地恢复为原连续信号。(8-6)二、理想采样过程为了简化采样过程的数学描述,引入如下理想采样开关的概念。载波信号可以近似成如下理想脉冲序列())(tp0kTkTtt)()((8-7)再设当时,则采样过程的数学描述为0t0)(tf此时,采样过程如图8-6所示。理想采样开关的输出是一个理想脉冲序列。0)()()()()(kTkTttfttftf(8-8)图8-6理想采样开关的采样过程同样,可以展成如下Fourier级数ntjnnTseCt)(()TtTCn1其中(8-10)ntjnsetfTtf)(1)(则有(8-11)nsjnjFTjF)(1)(和(8-12)图8-7连续信号和采样信号的频谱注意:上述香农采样定理要求满足以下两个条件:①频谱的上限频率是有限的;②存在一个理想的低通滤波器。但可以证明理想的低通滤波器在物理上是不可实现的,在实际应用中只能用非理想的低通滤波器来代替理想的低通滤波器;8-2信号的恢复与零阶保持器信号的恢复是指将采样信号恢复为连续信号的过程,能够实现这一过程的装置称为保持器。TktkT)1(可将)(tf展成如下泰勒级数时,nkTtnkTtkTttfnkTttfkTftf)()(!1)()()()()((8-13)返回子目录各阶导数的近似值由此类推,计算n阶导数的近似值需已知n+1个采样时刻的瞬时值。若式(8-13)的右边只取前n+1项,便得到n阶保持器的数学表达式。2)2()(2)()(TTkTfTkTfkTftfkTtTTkTfkTfkTf)()()((8-14)图8-8信号的采样与保持过程零阶保持器的数学表达式为TktkTkTftf)1()()((8-16)理想采样开关的输出Laplace变换为零阶保持器的输出为0)()(kkTsekTfsF(8-17)0)(1)(1)()(khTkTtkTtkTftf(8-18)由上式可知零阶保持器的0)1()()(kTskkTshseekTfsF0)(1kkTsTsekTfsesesGTsh1)((8-20)(8-19)传递函数零阶保持器的频率特性为jejGTjh1)(TjeTTT212/)2/sin(seTss//)/sin(sshTjG/)/sin()()/sin()(sshjG相频特性为(8-22)(8-23)其幅频特性为其中零阶保持器的频率特性曲线如图8-9所示,对比图8-4可知零阶保持器是一个低通滤波器,但不是理想的低通滤波器,它除了允许信号的主频谱分量通过外,还允许部分高频分量通过。0,2(21)sin(/),(21)2(1)(n0,1,2,)sssssnnnn图8-9零阶保持器的频率特性曲线8-3z变换与z反变换一、z变换连续信号经采样后得到的脉冲序列为)(tf对上式进行Laplace变换,得0)()()(kkTtkTftf(8-25)0)()(kkTsekTfsF(8-26)返回子目录引入一个新的复变量将式上式代入式(8-26)可得zz变换变换的定义式如下Tsez称为的zz变换变换,记作或)(zF)(tf)()]([zFtfZ)()]([zFkTfZkzkTfzTfzTfzfzF)()2()()0()(210由此可看出是关于复变量的幂级数。)(zF1z0ln)/1()()()(kkzTszkTfzFsF(8-28)例8-1求单位脉冲信号的z变换。)()(ttf)()()()(0tkTttftfk)(tf0t解:设,则由于在时刻的脉冲强度为1,其余时刻的脉冲强度均为零,所以有11)(0zzF例8-2求单位阶跃信号的z变换。解:设,则该级数的收敛域为,在该收敛域内,上式可以写成如下闭合形式)(1)(ttfkzzzzF211)(1z)1(,111)(1zzzzzF)1(,)1()(20zzTzzkTzFkk例8-3求单位斜坡信号的z变换。设,则上式两边对z求导数,并将和式与导数交换,得上式两边同乘,便得单位斜坡信号的z变换0)(kkzkTzF)0(,)(tttf)1(,10zzzzkk201)1(1)(zzkkk)(Tz解:例8-4求指数函数的z变换。解:设,则kakTTaaTzezezezF2211)()(,111aTaTaTezezzzeatetf)())(1()1(1)(TTTezzezezzzzzF例8-5设,求的z变换。)1(1)(sssF)(tf解:上式两边求Laplace反变换,得)0(,1)(tetft再由例8-2和例8-4有111)(sssF注意:zTsln1)(sF)(zF)(tf不能直接将代入来求,因为是针对采样信号进行z变换。二、z变换的基本定理其中和为任意实数。1a2a1.线性定理:11221122[()()]()()ZaftaftaFzaFz(8-30))(1tf)(2tf)(1zF)(2zF若和z变换为和,则证明:112211220[()()][()()]kkZaftaftafkTafkTz022011)()(kkkkzkTfazkTfa)()(2211zFazFa2.实数位移定理若的z变换为,则)(tf)(zF)()]([zFznTtfZn(8-31)])()([)([10nkknzkTfzFznTtfZ(8-32)证明:证明式(8-31)由于当时,,所以有njjnzjTfz)(0)()(knknznTkTfz0)()]([kkznTkTfnTtfZ0j0)(jTe0)()]([jjnzjTfznTtfZ)(zFzn证明式(8-32)0)()]([kkznTkTfnTtfZ0)()(knknznTkTfz100)()(nkkjjnzkTfzjTfz10)()(nkknzkTfzFz3.复位移定理已知的z变换函数为,则)(])([aTakTezFekTfZ证明:证明:0)(])([kkakTakTzekTfekTfZ0)()(kkaTzekTf)(aTezF)(kTf)(zF4.Z域尺度定理若已知的z变换函数为,则证明:证明:0)()]([kkkkzkTfakTfaZ0)(kkazkTfazF)(kTf)(zF其中,为任意常数。aazFkTfaZk)]([(8-34)三、z反变换z反变换是z变换的逆运算。其目的是由象函数求出所对应的采样脉冲序列(或),记作)(nTf)(zF)(tf)()]([tfzF-1Z(8-35)z反变换只能给出采样信号,而不能给出连续信号。)(tf)(tf注意1部分分式法若象函数是复变量z的有理分式,且的极点互异,则可展成如下形式:)(zF),,2,1(,miezTaiizzF)(上式两边同乘z,再取z反变换得TamTaTamezKezKezKzzF2121)((8-36)TamTaTamezzKezzKezzKzF1-1-1-1-ZZZZ2121)]([(8-37)nTamnTanTameKeKeKnTf2121)((8-38)zzF)(例8-6已知z变换函数求其z反变换。))(1()(TezzzzF解:首先将展成部分分式TezKzKzzF211)(TzezFzzK11)(1lim11zzF)(TTezezFzezKT11)(lim2TTezzzzezF111)(nTTeenTf111)(0)()1(11)(kkTTkTteetf2长除法kkzfzffzF110)(对比式(8-29)可知若z变换函数是复变量z的有理函数,则可将展成的无穷级数,即)(zF)(zF1z,2,1,0,)(kfkTfk(8-40)0)()(kkkTtftf(8-41)例8-7已知z变换函数为求其z反变换。)3)(2()(zzzzF()()5(2)19(3)65(4)fttTtTtTtT解:由65165)(112zzzzzzF运用长除法得432165195)(zzzzzF由此得,65)4(,19)3(,5)2(,1)(,0)0(TfTfTfTff于是脉冲序列可以写成3留数计算法由z变换的定义可知0)()(kkzkTfzFdzzkTfdzzzFkkmm011)()(dzzkTfdzzzFkmkm101)()(011)()(kkmmzkTfzzF(8-43)设的极点为,则1)(kzzFnizi,,2,1,1)(kzzF包围了的所有极点niikzzzFreskTf11],)([)((8-48)例8-8已知z变换函数为试用围线积分方法求z反变换。)2)(1(10)(zzzzF解:上式有两个极点和,且)2)(1(10)(1zzzzzFkk10)()1(lim]1,)([111kzkzzFzzzFreskkzkzzFzzzFres210)()2(lim]2,)([121)12(10)(kkTf),2,1,0(k所以11z22z四初值定理和终值定理1初值定理:设的z变换为,并且有极限存在,则)(kTf)(zF)(limzFz)(lim)0(zFfz(8-49)2终值定理:设的z变换为,且的极点均在z平面的单位圆内,则)(kTf)(zF)()1(1zFz)()1(lim)(lim10zFzkTfzk(8-50)五、用z变换法解线性常系数差分方程11差分的定义差分的定义假设在图8-1所示的采样系统中,模拟—数字转换器在离散时间对误差信号进行采样,并将瞬时值记为或,则的一阶前项差分定义为)(te)(kTeke)(kekekkkeee1二阶前向差分定义为n阶前向差分定义为n阶后向差分定义为)(2kkeekkee1kkkeee122knknkneee111111knknkneee8-4脉冲传递函数一、脉冲传递函数的定义脉冲传递函数定义为输出采样信号的z变换与输入采样信号的z变换之比)()()(zRzCzG(8-59)图8-10返回子目录系统输出的采样信号为)]()([)]([)(11zRzGZzCZtc经虚设采样开关得到的脉冲序列反映的是连续输出在采样时刻的瞬时值。)(tc)(tc二、开环脉冲传递函数1.开环脉冲传递函数的推导1()()sjktkrtrteT1()()skRsRsjkT)()()(sRsGsC0)()(1kssjksRjksGT0)(1)(ksjksCTsC)()(10sRjksGTks)()(sRsG0)(1)(ksjksGTsG)()()(zRzGzC(8-66)由此求该开环系统的脉冲传递函数。例8-11系统结构如图8-10所示,其中连续部分的传递函数为)11.0(1)(sssG)(zG解:连续部分的脉冲响应函数为)0()1()(10tetgtkTekTg101)(0)()(kkzkTgzG0101kkkTzeTezzzz101))(1()1(1010TTezzez脉冲传递函数为或由得)(sG1011)(sssG))(1()1(1)(101010TTTezzezezzzzzG查表得2.串联环节的脉冲传递函数(1)串联环节间无采样开关时的脉冲传递函数图8-11)()]()([)(2121zGGsGsGZzG(8-67)例8-12系统结构如图8-11所示,其中求开环脉冲传递函数。assG1)(1bssG1)(2解:bsasabsGsG111)()(2112()()1()()()aTbTaTbTGzGGzzeebazeze(2)串联环节间有采样开关时的脉冲传递函数如图8-12所示,其脉冲传递函数为各个连续环节z变换的乘积,记为图8-12串联环节间有采样开关的开环系统1212()[()][()]()()GzZGsZGsGzGz(8-68)例8-13系统结构如图8-12所示,其中求开环脉冲传递函数。1211(),()GsGssasb解:212()()()()()aTbTzGzGzGzzeze所以由于1122()[()]()[()]aTbTzGzZGszezGzZGsze212812zGzGGz1由例和例8-13可知,一般G()()()。(3)有零阶保持器时的脉冲传递函数开环脉冲传递函数为)(1)(sGseZzGTsTsesGsZsGsZ)(1)(1)(11)(1sGsZzzG图8-13带零阶保持器的开环采样系统例8-14系统结构如图8-13所示,其中采样周期s求其开环脉冲传递函数。)1()(ssKsG1T解:由于所以1111)(12sssKsGs1211)1(]1[)(ezzzzzzzKzG)368.0)(1()717.0(368.0))(1()21(111zzzKezzezeK三、闭环脉冲传递函数图8-14闭环采样系统采样开关的输入和系统的输出分别为)()()()()(sEsHsGsRsE)()()(sEsGsC)()()()(sEsGHERsE)()()(sEsGsC整理得于是闭环系统的脉冲传递函数为)()(1)()(sRsGHsGsC)()(1)()(zRzGHzGzC)(1)()()()(zGHzGzRzCz例8-15闭环采样系统的结构如图8-14所示,其中采样周期秒,求闭环脉冲传递函数,若,求。)1(1)(sssG1)(sH1T)(1)(ttr)(tc解:对于阶跃输入函数有)368.0)(1(632.0)()(zzzzGHzG368.0737.0632.0)()(2zzzzRzC1)(zzzR则输出信号的z变换为于是)368.0736.0)(1(632.0)(22zzzzzC1234560.6321.0961.2051.1201.0140.98zzzzzz()0.632(1)1.096(2)1.205(3)1.120(4)cttttt)6(98.0)5(014.1tt注意有些闭环采样系统不可能求出形式的闭环脉冲传递函数,而只能求出输出信号的表达式。如图8-15所示的闭环采样系统)()(zRzC)(zC(8-15)8-5采样系统的性能分析一、稳定性1从s平面到z平面的影射关系Tsez由Z变换的定义(8-80)js若令(8-81)TjTeez则有(8-82)返回子目录左半s平面上的带称为主带,其它称为次带。图8-16从s平面到z平面的影射22ss2Z域的稳定条件和稳定性判据在z平面上系统稳定的充分必要条件是,系统的特征根必须全部位于z平面的单位圆内。设采样系统的闭环脉冲传递函数为)()()()()(zDzMzRzCz则闭环特征方程为0)(zD(8-84)(1)朱利(Jury)稳定判据且,根据特征方程的系数构造朱利阵列,nnzazazaazD2210)(0na则特征方程0)(zD的根均位于单位圆内的充分必要条件为0)1()1(,0)1(DDn2020100qqccbbaannn共(n-1)个约束条件(8-86)(8-87)例8-16已知采样系统的闭环特征方程为试判断该系统的稳定性。325.175.0125.0)(zzzzD0375.3)1()1(,0125.0)1(3DD解:解:0z1z2z3z朱利阵列朱利阵列行数1-0.1250.75-1.5121-1.50.75-0.1253-0.981.41-0.564-0.561.41-0.96系统是稳定的30aa20bb(2)劳思(Routh)稳定判据在分析连续系统分析连续系统时,曾应用Routh稳定判据判断系统的特征根位于s右半平面的个数,并依此来判断系统的稳定性。对于采样系统采样系统,也可用Routh判据分析其稳定性,但由于在z域中稳定区域是单位圆内,而不是左半平面,因此不能直接应用Routh判据。引入如下双线性变换此时可用Routh判据判断采样系统的稳定性。11wwz(3)z平面的根轨迹方法以上述例8-15所示的闭环采样系统为例,其特征方程为0)(1zG)368.0)(1(632.0)(zzKzzG可知使系统稳定的最大K值为4.33。例8-16的根轨迹图二、闭环极点与瞬态响应之间的关系设采样系统的闭环传递函数为nnnnmmmmazazazabzbzbzbz11101110)()())(()())((210210nmpzpzpzazzzzzzb)()(zDzM1)()()()()(zzzDzMzRzzC(8-91)若输入信号为单位阶跃,则将按部分分式展开,得上式中第一项为稳态分量稳态分量,第二项为瞬瞬态分量态分量,显然瞬态分量的变化规律取决于极点在z平面中的位置。nkkkpzzczzDMzC11)1()1()(),2,1,0()1()1()(1mpcDMmTcnkmkkzzC)(图8-18不同极点所对应的瞬态响应三、稳态误差图8-19单位负反馈采样系统)()(11)(zRzGzE(8-97))(tr在输入信号作用下,误差的z变换表达式为1当输入为阶跃函数时)1/()(zzzR)(lim1zGKzp定义静态位置误差系数为pzKzzzGze111)(11)1(lim)(1则根据终值定理,有2当输入是斜坡函数时2)1/()(zTzzR)()1(lim1zGzKzv定义静态速度误差系数为vzKTzTzzGze21)1()(11)1(lim)(稳态误差为3当输入是等加速信号时32)1(2/)1()(zzzTzR)()1(lim21zGzKza定义静态加速度误差系数为azKTzzzTzGze2321)1(2)1()(11)1(lim)(稳态误差为例8-17已知采样系统的结构如图所示,其中,,采样周期s,求在输入信号的作用下,系统的稳态误差。)0(,5.01)1(2tttr2)15.0(2)(sssG2.0T图8-21解:3)15.0(21)(ssZzzzG322)1()1()1(1zzzTzTzzz2)1(16.024.0zz084.076.1)(2zzzD采样系统的闭环特征方程为采样系统的开环脉冲传递函数为008.0)1(D06.3)1(D184.020aa该采样系统稳定在阶跃和斜坡函数作用下的稳态误差为零静态加速度误差系数为08.0)16.024.0(lim)()1(lim121zzGzKzza5.008.004.00011)(2avpKTKTKe25.01)(tttr因此,在输入作用下的稳态误差为8-6采样系统的数字校正如图所示的闭环采样系统闭环脉冲传递函数为)()(1)()()(zDzGzDzGz图8-21含数字校正装置的采样系统返回子目录系统的误差为)()](1[)(zRzzE11)1()()(qzzBzR其中为的有限次多项式,若能选择合适的,使)(zB1z)(zD)()1()(111zzzq其中为关于的多项式,并且不含因子。)(z1z)1(1z0tq设输入为时间的幂函数Atq(),其中为正整数,则)()()1(lim)(11zBzzez则稳态误差为零。11)1(1)(qzz)(1)()(1)(zzzGzD(8-109)(8-110)将代入上式,便可确定所需要的数字校正装置的脉冲传递函数。)(z)(zD1)(z又为了使系统能在尽可能少的周期内实现对输入的完全跟踪,应使中所含项的数目最少,为此应取()z1z1当时最少拍无差系统的闭环传递函数为此时误差信号的Z变换为)(1)(ttr1)(zz1)(zE系统经过1拍便可以完全跟踪上输入信号。(8-111)(8-112)2当时最少拍无差系统的闭环传递函数为此时误差信号的Z变换为)(1)(tttr系统经过2拍便可以完全跟踪上输入信号。212)(zzz1)(TzzE(8-113)(8-114)3当时最少拍无差系统的闭环传递函数为此时误差信号的Z变换为系统经过3拍便可以完全跟踪上输入信号。(8-115)(8-116))(121)(2tttr32133)(zzzz22122121)(zTzTzE例8-18已知采样系统的结构如图所示,其中,采样周期s,,试设计使该系统在单位阶跃信号作用下为最少拍无差系统。1T)1(1)(sssG)(zD图8-21最少拍无差系统121)(kkzzzzC)368.0)(1(264.0368.0)1(1)1()(21zzzssZzzG解:将上式求Z反变换可得输出序列264.0368.0368.0)(zzzD本章主要知识点与主要线索稳态误差根轨迹开环脉冲传递函数()e闭环零、极点系统稳定性、品质系统型别(稳定系统)劳斯判据双线性变换终值定理()z()ez()Ez特征式D(z)()Dw稳定性一定条件下长除法部分分式分解求留数朱利判据闭环零、极点稳定性平稳性、快速性()Cz()ct()ct第七章非线性系统分析第7章非线性系统分析7-1非线性问题概述基本要求7-2常见非线性因素对系统运动特性的影响7-3相平面法基础7-4非线性系统相轨迹分析7-5描述函数7-6用描述函数分析非线性系统返回主目录基本要求①明确非线性系统动态过程的本质特征。掌握系统中非线性部分、线性部分结构归化的方法。②熟练掌握二阶线性方程的相轨迹,正确理解焦点、节点、中心、鞍点、极限环等概念。③熟练掌握由相轨迹计算时间的方法。已知相轨迹大致画出时间响应曲线的图形。④对简单的非线性系统能熟练写出相轨迹的解析表达式。能通过等倾线方法作出相轨迹。返回子目录⑤对分段线性的非线性系统,能决定开关线,写出分区域相轨迹的方程式。⑥对具有外作用和或具有速度反馈的情况能合适地选取相坐标作出相轨迹图。⑦正确理解谐波线性化的条件及描述函数的概念。⑧了解描述函数建立的一般方法,明确几种典型非线性特性负倒描述函数曲线的特点。⑨熟练掌握运用描述函数法分析系统中是否有周期运动,判断周期运动的稳定性。简介•非线性系统一般理解为非线性微分方程所描述的系统。•线性系统的本质特征是叠加原理,因此非线性系统也可以理解为不满足叠加原理的系统。本章将介绍工程上常用的相平面法和描述函数法,并通过这两种方法揭示非线性系统的一些区别于线性系统的现象。7-1非线性问题概述•一.实际系统中的非线性因素图7-1一些常见的非线性特性返回子目录•除上述实际系统中部件的不可避免的非线性因素外,有时为了改善系统的性能或者简化系统的结构,人们还常常在系统中引入非线性部件或者更复杂的非线性控制器。•通常,在自动控制系统中采用的非线性部件,最简单和最普遍的就是继电器。图7-2电磁继电器的工作原理和输入-输出特性二.非线性系统和线性系统有不同的运动规律①在线性系统中,系统的稳定性只取决于系统的结构和参数,对常参量线性系统,只取决于系统特征方程根的分布,而和初始条件、外加作用没有关系。对于非线性系统,不存在系统是否稳定的笼统概念。必须具体讨论某一运动的稳定性问题。非线性系统运动的稳定性,除了和系统的结构形式及参数大小有关以外,还和初始条件有密切的关系。②线性系统自由运动的形式与系统的初始偏移无关。非线性系统则不一样,自由运动的时间响应曲线可以随着初始偏移不同而有多种不同的形式。图7-4非线性系统在不同初始偏移下的自由运动③线性系统在没有外作用时,周期运动只发生在临界情况,而这一周期运动是物理上不可能实现的。非线性系统,在没有外作用时,系统中完全有可能发生一定频率和振幅的稳定的周期运动,如图7—5所示,这个周期运动在物理上是可以实现的,通常把它称为自激振荡,简称自振。图7-5非线性系统的自激振荡④线性系统中,当输入量是正弦信号时,输出稳态分量也是同频率的正弦函数,可以引入频率特性的概念并用它来表示系统固有的动态特性。非线性系统在正弦作用下的输出比较复杂。三.非线性系统的分析方法在线性系统中,一般可采用传递函数、频率特性、脉冲过渡函数等概念。在工程实际中对于存在线性工作区域的非线性系统,或者非线性不严重的准线性系统,常常采用线性化的方法进行处理,然后在线性分析的基础上加以修正。而对于包括像继电特性那样根本不存在线性区的非线性特性,工程上常用相平面方法和描述函数方法进行研究。7-2常见非线性因素对系统运动特性的影响一.不灵敏区不灵敏区又叫死区,系统中的死区是由测量元件的死区、放大器的死区以及执行机构的死区所造成的。图7-6死区特性返回子目录死区非线性特性的数学表达式如下:011112xsignxxKxx0101111xxsignx式中图7-7包含死区的非线性系统图7-8斜坡输入时的系统输出量二、饱和图7-9部件的饱和现象•饱和特性也是系统中最常见的一种非线性特性。理想化后的饱和特性典型数学表达式为:•式中:•a是线性范围,K为线性范围内的传递系数(对于放大元件,也称增益)。12111KaxaxKxxaKaxa粗略地看,饱和特性的存在相当于大信号作用时,增益下降。图7-10饱和特性图7-11饱和特性的等效增益图7-13图7-12系统的响应随动系统的方块图如图7—12所示。当系统输入端加上一个幅值较大的阶跃信号时,若放大器无饱和限制,系统的时间响应曲线如图7-13中的曲线1;放大器有饱和限制时的时间响应曲线如图7-13中的曲线2。图7-12非线性系统若随动系统的方块图如图7—15所示。图7-14根轨迹图图7-15非线性系统根轨迹分析:图7-16系统的时间响应当系统中不存在饱和特性的限制,系统是振荡发散的;若系统中存在饱和特性的限制,则系统不再发散,而是出现稳定的等幅振荡,如图7-16中的曲线2。三、间隙图7—17齿轮传动中的间隙传动机构(如齿轮传动、杆系传动)的间隙也是控制系统中的一种常见的非线性因素。间隙特性的典型形式如图7-18所示bxKxxbxKxbsignxxKx012212112(7-6)•数学表达式为图7—18间隙非线性特性•间隙对系统性能的影响也很复杂,一般说来,它会增大系统的静差,使系统波形失真,过渡过程的振荡加剧。图7-19间隙特性的输入-输出波形四、摩擦图7-20直流电动机的方框图摩擦非线性对小功率角度随动系统来说,是一个很重要的非线性因素。它的影响,从静态方面看,相当于在执行机构中引入了死区,从而造成了系统的静差,这一点和死区的影响相类似。图7-21摩擦力矩示意图图7-22小功率随动系统方框图图7-23低速爬行现象7-3相平面法基础•相平面法是一种求解二阶常微分方程的图解方法。设一个二阶系统可以用下列常微分方程描述),(xxfxxx1xx2令,(7-9)则22112),(xxxfdxdx(7-11)返回子目录相平面:描绘相平面上的点随时间变化的曲线叫相轨迹。通常把方程(7-9)称为相轨迹微分方程式,简称相轨迹方程。将(7-11)式的积分结果称为相轨迹表达式。相轨迹:(x,x)把具有直角坐标的平面叫做相平面。一、线性系统的相轨迹•设系统的微分方程为022xxxnn(7-12)0222nns系统(7-12)的特征方程为12nn上述特征方程的根为式(7-12)所表示的自由运动,其性质由特征方程根的分布特点所决定。取相坐标、,式(7-12)可化为:xx2(2)nndxxxdtdxxdt(7-14)或22nnxxdxdtx(1)无阻尼运动由方程(7-14),相轨迹方程为:)0(22002nxAx其中相轨迹如图7-24所示,在相平面上是为一族同心的椭圆。每个椭圆相当于一个简谐振动。2222()()nxtxtA(7-16)图7-24系统无阻尼运动时的相轨迹相轨迹的方向如图7-24中箭头所示。相轨迹垂直穿过横轴。坐标原点处相轨迹的斜率不能由该点的坐标唯一地确定,这种点叫做奇点。图7-24的奇点(0,0)通常称为中心(2)欠阻尼运动10其中22000ndxxAx000ndxxarctgx()sin()ntdxtAet(7-17)方程(7-12)的解为•相轨迹如图7-25所示。从图中可以看出,欠阻尼系统不管初始状态如何,它经过衰减振荡,最后趋向于平衡状态。坐标原点是一个奇点,它附近的相轨迹是收敛于它的对数螺旋线,这种奇点称为稳定的焦点。图7-25系统欠阻尼运动时的相轨迹(3)过阻尼运动这时方程(7-12)的解为11212()qtqtxtAeAe002112xxA001212xxA121122()qtqtxtAqeAqe相轨迹如图7-26所示。图7-26过阻尼时的相轨迹图7-27过阻尼运动的时间响应坐标原点是一个奇点,这种奇点称为稳定的节点。(4)负阻尼运动•相轨迹图如图7-28所示,此时相轨迹仍是对数螺旋线,但相轨迹的运动方向与图7-25不同,随着t的增长,运动过程是振荡发散的。这种奇点称为不稳定的焦点。01图7-28•系统的相轨迹图如图7-29所示,奇点称为不稳定的节点。1图7-29•此时相轨迹如图7-30所示。奇点称为鞍点该奇点是不稳定的。022xxxnn图7-30斥力系统的相轨迹图7-31特征根和奇点的对应关系二、相轨迹作图法),(xxfx设系统微分方程如xxxfdxxd),(化为表示相平面上的一条曲线,相轨迹通过曲线上的点时所取的斜率都是a这条曲线就称为等倾线。axxxf),(令其中为某个常数a1等倾线法例子•微分方程0xxxxxxdxxd或xax11等倾线是直线,它的方程为:取不同值时,可在相平面上画出若干不同的等倾线,在每条等倾线上画出表示该等倾线斜率值的小线段,这些小线段表示相轨迹通过等倾线时的方向,从相轨迹的起点按顺序将各小线段连接起来,就得到了所求的相轨迹。a图7-32图7-34各种类型的极限环极限环在图7-33中,出现了一种孤立的简单的封闭相轨迹。这种相轨迹称为稳定的极限环。2(1)0xxxx1图7-33图7-34各种类型的极限环三、由相平面图求时间解•相轨迹上坐标点移动到点所需的时间,可按下式计算1x2x2112xxxdxtt(7-37)这个积分可用通常近似计算积分的方法求出,因此求时间解的过程是近似计算的过程。1、用曲线计算时间利用式(7-37)计算时间,在某些情况下可直接进行积分运算。1/x图7-372、用小圆弧逼近相轨迹计算时间•在小圆弧逼近的方法中,相轨迹是用圆心位于实轴上的一系列圆弧来近似的。PAxQBRC如图7-8AD段,可用轴上的P、Q、R点为圆心,以、、为半径的小圆弧来逼近,这样就有ADABBCCDABBCCDttttttt••代入(7-37)式得sinPAxcosPAOPx令sinsinBABAABABPAtdPA(7-38)•图7-38用小圆弧逼近相轨迹计算时间例7-2•图示相平面上有两条封闭的相轨迹,已知和均是圆弧的一部分,试计算这两条封闭相轨迹所对应的周期运动的周期。AB11AB图7-39解:•相轨迹和对应的周期运动,他们的周期分别为和s,•则有ABCD1111ABCDT1T12(2)4,22(12.21)6.43TT7-4非线性系统相轨迹分析①根据系统结构形式选取相坐标,列写微分方程。②画相轨迹图③根据相轨迹图分析系统的运动情况。返回子目录一、继电型系统•系统中有一个或几个元件具有继电型非线性特性的系统称为继电型系统。图7-40继电型非线性特性若继电系统的方框图如图7—41所示•研究图中继电特性为图7-40(b)的情况图7-41•很明显,相平面以直线为界被分成三个不同的区域,在每个区域里,系统的相轨迹完全由一个线性微分方程所确定ec时hcKMhchcKMtctcT0)()(ch1在c>h的区域KMtctcT)()(系统方程为TKMcck)(001TKMck)(02其中(1/)12()TtctkkeKMtKMtc)(所以KMc0当(1/)0()()TtctcKMeKM2在ce0时的相轨迹图7-55kKe0Ke0,R=0返回子目录7-5描述函数•描述函数可以定义为非线性特性输出的一次谐波分量与输入正弦量的复数比。若输出的一次谐波分量为)sin(sincos)(11111tYtBtAty输入的正弦量为tXsin则描述函数的数学表达式如式(7-75)所示:22111111arctanABYANXXB(7-75)图7-57理想继电特性在正弦输入时的输出波形和振幅频谱其中201)(cos)(1ttdtyA201)(sin)(1ttdtyB)(tytXsin为非线性特性在输入信号作用下的输出。22111111()arctanABYANXXXB例7-3•若非线性特性为(7-76)34121xxy)(sin)4121(13201ttdxxXXBN•其特性曲线如图7-58。令tXxsin)(sin)sin41sin21(13320ttdtXtXXN)(sin2)(sin140220ttdXttd2116321XXBNtXXtysin)16321()(2则有图7-58式(7-76)的输入-输出特性图7-59描述函数一、不灵敏区特性的描述函数1sinX)/arcsin(1X2/11)(sin)sin(4ttdtXKB)(sin)(sin[42/2/211ttdXttdKX(7-83)•根据描述函数的定义,可求出不灵敏区的描述函数为12()2arcsin12BNXXKXXXX图7-60不灵敏区特性及其输入-输出波形二、饱和特性的描述函数SX1sinXSarcsin11102/21)(sin)(sin4ttdKSttdKXB2/011cossin41214tXSttKX21arcsin2XSXSXSKX)(SX•图7—61表示了饱和特性和它在正弦信号作用下的输出波形。•饱和特性的描述函数为21arcsin2)(XSXSXSKXN)(SX从上式可知,饱和特性的描述函数是输入幅值的实值函数,与输入频率无关。图7-61饱和特性及其输入-输出波形三、间隙特性的描述函数)21arcsin(1Xb2/01)(cos)sin(2ttdbtXKA112/)(cos)sin()(cos)(ttdbtXKttdbXK12/2/02/02sin)(sinsin212tbXKtKbtKX11sinsin212tKbtKX)(14bXXbbK2/01)(sin)sin(2ttdbtXKB112/)(sin)sin()(sin)(ttdbtXKttdbXK12/2/02/0cos)(cos2sin41212tbXKtKbttKX11cos2sin4121tKbttKXXbXbXbXbKX121221arcsin2)(bX间隙特性的描述函数为•图7—62表示了间隙特性和它在正弦信号作用下的输出波形XbXbXbXbK121221arcsin2XAjXBxN11)(14XbXKbjXb图7-62间隙特性及其输入-输出波形四、继电型特性的描述函数Xharcsin1Xharcsin3Xmharcsin2Xmharcsin24图7—63表示了具有滞环和不灵敏区的继电特性和它在正弦信号作用下的输出波形XhXmhXhXmhM)(,)1(2hMmXMh2143)(cos)(cos11ttdMttdMA4321sinsinttM2143)(sin)(sin11ttdMttdMB4321coscosttM22112XhXmhM)(hX继电特性的描述函数为•可知具有滞环和不灵敏区的继电特性的描述函数,和输入信号的频率无关,只是输入幅值的复数值函数。22112)(XhXmhXMXN)(hX122mXMhj图7-63继电特性及其输入-输出波形当h=0,两位置理想继电特性的描述函数XMXN4)(当m=1,三位置理想继电特性的描述函数)(,14)(2hXXhXMXN当m=-1,得到具有滞环的两位置继电特性的描述函数)(,414)(22hXXMhjXhXMXN返回子目录7-6用描述函数法分析非线性系统•非线性控制系统可化为下列结构形式图7-64非线性控制系统用描述分析非线性系统时两个基本假设:①系统的线性部分G(jω)具有很好的低通滤波性。②系统若发生自激振荡(稳定的周期运动),假定非线性环节N的输入端的振荡为正弦波。一、特征方程的解法•图7-64所示系统的特征方程为0)()(1jGXN(7-90)0X0如果对于某一个和,式(7-90)成立,那么非线性环节N输入端将有的周期运动。)sin(00tX此时相当于将整个)(/1XN曲线当作临界点。二、自激振荡的确定图7-65周期运动的确定及稳定性判别)(/1XN)(jG•分别将和曲线画在复平面上,如图7-65所示。•M1对应的周期运动为X01sinω01t•M2对应的周期运动为X02sinω02t。•M1的周期运动是不稳定的。M2的周期运动是稳定的。上述方法适用于G(s)无右半复平面极点的情形。)(jG)(/1XN图中曲线和曲线分别相交于M1点和M2点。图7-66不稳定的和稳定的周期运动M1对应周期运动稳定,M2对应周期运动不稳定图7-67jGK0当有不稳定根时,周期解的稳定性判断,需要用乃奎斯特判据。解析法00式(7-98)中的偏导数均在X0、处取值。则X0、对应的周期运动是稳定的,否则就是不稳定的周期运动。),(),()()(1XjBXAjGXN令(7-97)设式(7-97)有解X0和0,若有下式成立0XBABXA(7-98)三、分析系统自激振荡的例题•例7-4研究如图所示非线性系统。试判断系统是否存在自振;若有自振,求出自振的振幅和频率。图7-68解:描述函数为214)(XhXMXN43.20hMK141220hXhXXNhXhX计算数据表Xh-2-1.64-1.57-1.6410.90.80.6-1.81-2.14-2.74-4.18-7.890.50.40.30.20.1)(10xN)(10xNXh210.4780.9421.4062.2342.7493.8675.708-211-198.4-190.2-180-175.2-166.9-156.90.1970.3880.5790.9201.1321.5932.351400300250200180150120jGjG0jGK图7-69图7-68系统的曲线四、系统稳定性分析图7-72非线性系统的稳定性分析本章主要知识点与主要线索作图积分求解开关线结构归化计算查表非线性系统典型结构乃氏曲线线性部分分段线性的非线性系统分段相迹方程奇点类型相迹方程等倾线法稳定性,自振,求自振参数求时间1()NX()NX相迹时间响应第九章状态空间分析方法第9章状态空间分析方法基本要求9-1状态空间方法基础9-2线性系统的可控性和可观性9-3状态反馈和状态观测器9-4有界输入、有界输出的稳定性9-5李雅普诺夫第二方法返回主目录引言引言:前面几章所学的内容称为经典控制理论;下面要学的内容称为现代控制理论。两者作一简单比较。经典控制理论(50年代前)现代控制理论(50年代后)研究对象单输入单输出的线性定常系统可以比较复杂数学模型传递函数(输入、输出描述)状态方程(可描述内部行为)数学基础运算微积、复变函数线性代数、矩阵理论设计方法的特点非唯一性、试凑成份多,经验起很大作用。主要在复数域进行。设计的解析性,与计算机结合,主要在时间域进行。基本要求基本要求①掌握由系统输入—输出的微分方程式、系统动态结构图、及简单物理模型图建立系统状态空间模型的方法。②熟练掌握矩阵指数的计算方法,熟练掌握由时域和复数域求解状态方程的方法。熟练掌握由动态方程计算传递函数的公式。③正确理解可逆线性变换,熟练掌握可逆线性变换前、后动态方程各矩阵的关系。④正确理解可控性和可观测性的概念,熟练掌握和运用可控性判据和可观性判据。返回子目录⑤熟练掌握可逆线性变换矩阵的构成方法,能将可控系统化为可控标准形。能将不可控系统进行可控性分解。⑥正确理解对偶原理,会将原系统的有关可观测性的问题转化为对偶系统的可控性问题来研究。⑦正确理解单变量系统零、极点对消与动态方程可控、可观测的关系。熟练掌握传递函数的可控性标准形实现、可观性标准形实现的构成方法。⑧正确理解状态反馈对可控性,可观性的影响,正确理解状态反馈可任意配置闭环极点的充要条件。⑨熟练掌握全维状态观测器的公式和设计方法,熟练掌握由观测器得到的状态估计值代替状态值构成的状态反馈系统,可进行闭环极点配置和观测器极点配置。⑩正确理解系统齐次方程渐近稳定和系统BIBO稳定的概念,熟练掌握判别渐近稳定的方法和判别系统BIBO稳定的方法。⑪正确理解李雅普诺夫方程正定对称解存在的条件和解法,能通过解李雅普诺夫方程进行稳定性分析。9-1状态空间方法基础•在经典控制理论中,用传递函数来设计和分析单输入、单输出系统。•在现代控制理论中,用状态变量来描述系统。采用矩阵表示法可以使系统的数学表达式简洁明了,为系统的分析研究提供了有力的工具。返回子目录状态:动力学系统的状态可以定义为信息的集合。一、状态空间的基本概念已知时状态,时的输入,可确定时任一变量的运动状况。0t0tt0tt状态变量:确定动力学系统状态的最小一组变量。)(,),(1txtxn12nxtxtXtxt状态空间:由张成的n维向量空间。)(tX状态向量:如果完全描述一个给定系统的动态行为需要n个状态变量,那么状态向量定义为X(t)对于确定的某个时刻,状态表示为状态空间中一个点,状态随时间的变化过程,构成了状态空间中的一条轨迹。例9-2•设一RLC网络如图所示。回路方程为()1()()()ditetRitLitdtdtC图9-2RLC网络2()()xtitdt)()(1titx选择状态变量11211RxxxeLLCL则有21xx11010RuLCLLxx写成21)()(xCtcty10Cx输出11100RLLuLCxx写成)()(1titx21()()xtitdtC若选另一组状态变量11211()RxxxetLLL121xcx则有uyayayaynnnnn02211若给出(t=0)时的初值、、…、和时就可确定系统的行为。0,ttu)0(y)0(y)0()1(ny121,,,nnyxyxyx单输入-单输出线性定常系统选取状态变量二、系统的状态空间表达式12231nnxxxxxx(9-17)01121nnnxaxaxaxu或写成xAxBx12012101000001000,,00010nnxxxaaaaxAB(9-19)系统结构图如图所示图9-3例9-3222yyyu输入为u,输出为y。试求系统的状态方程和输出方程。考虑用下列常微分方程描述的系统解:12222122xxxxxu1122220102xxuxx状态方程为写成取状态变量12,xyxy输出1210xyx图9-4例9-3系统的结构图多输入-多输出系统图9-6多变量系统ppnnububxaxaxax111112121111ppnnububxaxaxax212122221212………pnpnnnnnnnububxaxaxax112211nxxx,,,21为状态变量;puuu,,,21为输入量;qyyy,,,21为输出变量。矩阵形式:xAxΒu111212122212nnnnnnaaaaaaaaaA111212122212ppnnnpbbbbbbbbbB式中ppnnududxcxcxcy111112121111ppnnududxcxcxcy212122221212……….pqpqnqnqqqududxcxcxcy112211输出变量方程111212122212nnqqqncccccccccC111212122212ppqqqpdddddddddDyCxDu式中式中图9-7系统结构图三、线性定常系统状态方程的解式中均为列向量。)2,1,0(ibixAx(9-28)齐次向量微分方程kktbtbtbbtx2210)((9-29)方程的解为1、齐次状态方程的解)(210121kkkktbtbbAtkbtbb可得()txxAx代入方程将方程两边系数必相等,即102210332001122113321kkbAbbAbAbbAbAbbAbk!0)0(bx我们定义022)121()(xtAktAAtItxkk!!(9-31)kKAttAktAAtIe!!12122(9-32)因此,齐次状态方程的解为将t=0代入(9-29)中得0)(xetxAt(9-33)()()xtAxt(9-34))()(0sAxxssx(9-35)Ate为n×n矩阵,称矩阵指数。于是齐次状态方程的解为用拉氏变换法求解01)()(xAsIsx011])[()(xAsILtx])[(11AsILeAt122311()[][]AtkkkksIALeLIAtAtkIAAAssss!拉氏反变换后得到(9-37)(9-38)最终得到•与前一种解法所得结果一致。AtetAtexp式中()(0)()(0)Atxtextx(9-41)状态转移矩阵具有以下性质:I)0(,1)()(,21tt)()()(,3020112tttttt)()]([,4kttk图9-8状态转移特性性质性质33例9-511220100xxxx设系统的状态方程为试求状态转移矩阵。解:2211()2!!AtkkteIAtAtAtk230100,00001001()010001nAAAAttt11221()(0)01()(0)txtxxtx求状态转移矩阵为其中可以写出方程解为例9-6x3210x设系统状态方程为试求状态方程的解。解:2s21s12s21s22s11s12s11s2)2s)(1s(s)2s)(1s(2)2s)(1s(1)2s)(1s(3ss213s)2s)(1s(1AsI)AsI(adj)AsI(3s21s)AsI(1用拉氏变换求解。先求出矩阵指数状态方程之解为t2tt2tt2tt2t11Ate2ee2e2eeee2])AsI[(Le)0(x)0(xe2ee2e2eeee2)0(xe)t(x21t2tt2tt2tt2tAt将上式进行拉氏反变换图9-9系统的瞬态解(a)与相轨迹(b)改写为)()()(tButAxtx用左乘等式两边Ate2非齐次状态方程的解非齐次方程)()()(tButAxtx(9-53))()]([)]()([tBuetxedtdtAxtxeAtAtAt(9-54)dBuextxetAAt)()0()(0dBuexetxttAAt)()0()(0)(用左乘上式两边Ate(9-54)0()()(0)()()txttxtBud则式(9-54)可以写成(9-55)积分上式得讨论非齐次状态方程的拉氏变换解法sBusAxxssx)()(0sBuAsIxAsIsx101)()()()]()[()0(])[()(1111sBuAsILxAsILtx拉氏反变换得])[(11AsILeAt由于ttAdBuesBuAsIL0)(11)(])[(由卷积定理有ttAdBuesBuAsIL0)(11)(])[(tAAtdtBuexetx0)()0()(ttAAtdBuexetx0)()()0()(因此由于最后得到例9-7uxx103210求下述系统状态的时间响应控制量u为单位阶跃函数。解:112222()2222tttttttttLsIAeeeeeeee)2)(1()2)(1(2)2)(1(1)2)(1(3][1ssssssssssAsI由状态转移矩阵tttttAeeeedtBue0225.05.0)(tttteeeexttx225.05.0)0()()(220.50.5()tttteextee若初始状态为零状态,则)()()(sBUsAXssX)()()(sDUsCXsY四、传递函数矩阵BuAxx(9-58)系统状态方程DuCxy(9-59)输出方程拉氏变换为解出定义传递函数矩阵为)()()(1sBUAsIsX)(])([)(1sUDBAsICsYAsIAsIadjAsI)()(1DBAsICsG1)()((9-63)所以特征方程为AsIDAsIBAsICadjDBAsIAsIadjCsG)()()(0AsI例9-8•设系统的动态方程为•试求该系统的传递函数矩阵。1112221122011002011001xxuxxuyxyx解:011010,,,0020101ABCD已知11111(2)()2102sssssIAoss故1()()111010(2)010110211(2)102GsCsIABssssssss例9-90100001061161Ab设系统的状态方程为试求系统的特征方程和特征值。解:3210det01611606116(1)(2)(3)0ssIAssssssIAsss系统的特征方程为特征方程的根为-1、-2和-3。矩阵A的特征值也为-1、-2和-3。两者是一样的。五、动态方程的可逆线性变换DuCxyBuAxxuDxCyuBxAxxPx1Pxx其中P是n×n矩阵1PAPA1CPCBPB特征多项式AsIAsIPPAsIPPPAsIPPAsIPPAPsPPPAPsIAsI1111111)(特征多项式没有改变。DBAsICDPBPAsIPCPDPBPAsIPCPDPBPAPsPPCPDPBPAPsICPDBAsIC111111111111111)()(])([)()()(传递函数阵传递函数阵没有改变例9-10•对例9-9之系统进行坐标变换,其变换关系为•试求变换后系统的特征方程和特征值。112233111123149xxxxxx解:根据题意求变换矩阵11111132.50.5123,34114911.50.5PPxPAPxPbu代入132(1)(2)(3)61160sIPAPssssss特征方程为特征值为-1,-2,-3,与例9-9结果相同。可得9-2线性系统的可控性和可观测性•在状态空间法中,对系统的描述可由状态方程和输出方程来表示。•状态方程是描述由输入和初始状态所引起的状态的变化;输出方程则是描述由于状态变化而引起输出的变化•可控性和可观测性的概念,就是回答“系统的输入是否能控制状态的变化’’和“状态的变化能否由输出反映出来’’这样两个问题。返回子目录一、准备知识设A是n×n矩阵,x是n×1向量,齐次方程组若A=0,(9-70)式存在非零解;若A≠0,(9-70)式只有零解。Ax=0(9-70)1、齐次方程组的非零解2、Cayley-Hamilton定理Cayley-Hamilton定理指出,矩阵A满足自己的特征多项式。则A满足1110()nnnfIAaaa(9-71)0)(0111IaAaAaAAfnnn(9-72)A的特征多项式应用Cayley-Hamilton定理)(0111IaAaAaAnnn10)(nkkkAtAte(9-78)120,,,nnAAAAI,Ate)(,nkAk对于矩阵指数可以用来表示。例9-11解:矩阵A的特征多项式22(1)21IA1201A100?A要求计算矩阵的矩阵A满足自己的特征多项式,有2324323243(1)nAAIAAAAIAAAAIAnAnI10012001009901AAI本题中n=100,故有3引理nbAbAAbbrankn][12的充分必要条件是:存在使01t101),0(ttATAtdtebbetWT(9-80)非奇异。这里A:n×n,b:n×1.若对任意状态,存在一个有限时刻和控制量,能在时刻将状态转移到0,则称此系统的状态完全可控。)(0tx0ttf)(tuft)(0tx二、线性系统的可控性1定义对于任意时刻和,若存在控制向量,能将的每个初始状态转移到时刻的另一任意状态,则称此系统的状态完全可控。)(tu0tft0ttftt)(0tx()fxt等价的定义例如图9-10二维系统状态转移过程如图所示系统可控。2可控性判据其中A(n×n),b(n×1),c(1×n),d(1×1)系统可控的充分必要条件是ducxybuAxx(9-84)(9-85)nbAAbbrankn1(9-86)单变量线性定常系统证明:将u(t)代入式(9-54),可得]xex)[t,0(Web)t(u1At0f1tATfT(9-87)若式(9-86)成立,由前面准备知识的引理,存在t1>0,使得(1-30)式定义的W(0,t1)矩阵非奇异,取t1为可控性定义中的tf,且在[0,tf]上定义由定义可知式(9-86)成立时,系统可控。ffTfft01At0f1AT)t(A0Atfd]}xex)[t,0(Web{bexe)t(x11AtAt0At0At1Att0f1ATAAt0t0f1ATAAt0Atxxeexexedxe)t,0(Webbeedx)t,0(WebbeexeffffffTffTff再证明若系统可控,则式(9-86)成立根据凯莱—哈密尔顿定理d)(bue)0(xft0A(9-88)1n0mmmAA)(e(9-89)假定系统由任意初始状态被控制到零状态,即x(tf)=0。根据(9-54)式,则有把(9-89)式代入(9-88)式,得记d)(u)(bA)0(xft0m1n0mm0()()(0,1,2,,1)ftmmudumnm1n0mmubA)0(x这时0111(0)nnuuxbAbAbu(9-90)由于x(0)是任意的n维向量,(9-90)式要有解,一定有(9-86)式成立,即n)bAbAAbb(rank1n2由上述可控性判据可知,系统的可控性只取决于(9-84)式中的A阵和b阵。今后为了方便起见,将可控性矩阵记为S,这样,可控的充要条件就写成:rankS=n或detS≠0。图9-11不可控系统例子系统可控uxx1100410201229414212102bAAbbPc01detcP系统3约当型方程的可控性判据约当块的一般形式为111111001由前面讨论可知,等价变换不改变可控性。可控的充分必要条件为①同一特征值对应的约当块只有一块,即各约当块的特征值不同。②每一约当块最后一行,所对应的b中的元素不为零。这一充分必要条件又称为单输入系统约当形方程的可控性判据。例9-12ubbbbx11x43212211系统状态方程为i21b,,试确定系统可控时,应满足的条件。解:0bb)(4221如果用直接计算可控性矩阵的方法也可得到同样结果.因为A阵有两个若当块,根据判据的(1)应有,由判据的(2),A的第二行所对应的b中的元素b2,b4均不为零,因此系统可控的充要条件为214、可控标准形uxxn100010000010000101210(9-92)则系统一定可控。一个单输入系统,如果具有如下形式(9-92)式的形式被称为单输入系统的可控标准形可控标准形。•对于一般的单输入n维动态方程(9-93)•其中A,b分别为n×n,n×1的矩阵。成立以下定理:若n维单输入系统可控,则存在可逆线性变换,将其变换成可控标准形。buAxx下面给出变换矩阵P的构成方法①计算可控性矩阵S;②计算,并记的最后一行为h。③构造矩阵P④令1S21nhhAPhAhAPxx1S1PAPAPBB1CPCDD即可求出变换后的系统状态方程。例9-13•设系统状态方程为•试将系统状态方程化为可控标准形。u110x041020122x解:•先判断可控性,再计算变换矩阵,将状态方程化为可控标准形。•故系统可控。•一定可将它化为可控标准形。0Sdet941421210bAAbbS2此时标准形中的系统矩阵的最后一行系数就是A阵特征式的系数,但符号相反。则变换矩阵为112h112225012S1102121012P324223112P1可求出1211221210322020121423140201010001254APAP100110324223112Pbb5系统按可控性进行分解•系统可控时,可通过可逆线性变换变换为可控标准形,现在研究不可控的情况,这时应有nnbAAbbrank11n下面的结果被称为系统按可控性进行分解的定理若单变量系统(9-84,85)式的可控性矩阵满足(9-103)式,则存在可逆线性变换矩阵P,使得变换后的系统方程具有以下形式式中是n1维向量,是n2维向量,并且121114221122(9104)00(9105)AAxbxuAxxxyccdux111n1111nbAbAbrank1db)AsI(cdb)AsI(c111n111(9-106)(9-107)1x2x(9-106)式表明下面的动态方程是可控的:•(9-107)式表明的动态方程式(9-108,109)和原来的n维动态方程式(9-84,85)具有相同的传递函数。或者说传递函数中未能反映系统中不可控的部分。duxcyubxAx111111(9-108)(9-109)证明:nnbAbAbAAbbrank11nn1n11(9-110)考察(9-103)式,并将它重新写出如下11nnbAAbbrank1进而可以证明1nn21q,,q,q补充选取线性无关的向量11,,,,,,,211nnnqqqbAAbb并使得向量组线性无关。令]q,,q,q,bA,,Ab,b[P11nn211n1若将(9-104,105)式所表示的系统用方框图表示,可控性分解的意义就能更直观地体现出来,(9-104,105)式的系统方块图如图9-12所示。Pbb,PAPA1即可证明具有定理所要求的(9-104)的形式。图9-12系统按可控性分解•从图9-12中可见,控制输入不能直接改变也不能通过影响间接改变,故这一部分状态分量是不受输入影响的,它是系统中的不可控部分。•由图上还可看出系统的传递函数完全由图中虚线以上的部分所决定,即传递函数未能反映系统的不可控部分。1x2x2x例9-14•设有系统方程如下•其传递函数为•试进行可控性分解。x001yu010x110010011x2)1s(1)s(g解:210111210bAAbbS2系统的可控性矩阵由于S的第3列是第1列与第2列的线性组合,系统不可控。1(001)Tq选取计算出1010110011PbAbq010cPc,001Pbb,100021010PAPA11构成110100101P故有因而得10c01b2110A11121001rankbAbrank111)s(g)1s(1012s11s10b)AsI(c211111三、线性系统的可观测性设n维单变量线性定常系统的动态方程为cxy,buAxx(9-113,114)如果在有限时间间隔[0,t1]内,根据输出值y(t)和输入值u(t),能够唯一确定系统的初始状态x(0)的每一个分量,则称此系统是完全可观测的,简称可观的。式中A,b,c分别为矩阵。1、可观测性的定义,1,1nnnn若系统中至少有一个状态若系统中至少有一个状态变量是不可观测变量是不可观测((不能被确定不能被确定))的,的,则称系统不可观。则称系统不可观。图9-13不可观测系统分析(9-117)式,当知道某一时刻的输出时,(9-117)式是n个未知量x(0)的(一个)方程,显然不能唯一确定初值,要解出x(0),必须要利用一段时间上的输入和输出的值。将(9-117)式左乘一个列向量,再从0到t1积分就可得到n个未知数x(0)的n个方程。就可利用线性方程组存在唯一解的条件来研究。()0()()(0)()tAtAtgtcxtcexcebud(9-117)我们考虑没有外作用的系统,可求出2可观测性判据可观测的充分必要条件是ncAcAcrank1n(9-118)(9-118)式中的矩阵称为可观性矩阵。并记为V。式(9-118)又可以写成det0Vn]c)A(c)A(cAc[rankT1nTT2TTTT取x(0)=α,这一非零的初始状态引起的输出为AtAtce)0(xce)t(y(9-120)0dtcecedet)t,0(VdetAtt0TtA11T根据准备知识中的引理,存在将代入上式,得显然α不可能由y(t)=0来确定。即系统不可观测。1n0kkkAtA)t(e100111()()(0)()()()0nkkknnytctAxccAtttcA20301110xxuyx试判断系统的可观测性。设系统动态方程为例题9-15解:•系统的可观性矩阵是奇异的,故系统不可观测。0201cAcV•系统可观性矩阵的秩,在对系统作可逆线性变换下保持不变,因而可逆线性变换不改变系统的可观测性。事实上111n1n111111nVPPcAcAc)PAP(cPPAPcPcPAcAccV1P因为是可逆阵,所以上式两端矩阵的秩相同。因为是可逆阵,所以上式两端矩阵的秩相同。3对偶原理•上面两个系统的系统矩阵、输入矩阵、输出矩阵之间有确定的关系,称系统Ⅰ、Ⅱ是互为对偶的系统。cxy,buAxxzbw,vczAzTTT系统Ⅰ系统Ⅱ对偶原理•系统Ⅰ的可控性(可观性)等价于系统Ⅱ的可观性(可控性)。•只要写出系统Ⅰ的可控性矩阵(可观性矩阵)和系统Ⅱ的可观性矩阵(可控性矩阵)即可证明以上结论。•利用对偶原理,可以将可控性的研究结果应用到可观测性的研究上。因为对对偶系统的可控性研究就相当于对原系统的可观性研究。应用:•若式(9—113)和式(9—114)的动态方程中A阵具有约当标准形,则系统可观测的充分必要条件为①同一特征值对应的约当块只有一块。②每一约当块的第1列所对应的c中的元素非零。上述条件就是约当形动态方程的可观测性判据。它可以由对偶系统的可控性判据得到。例9-16•设动态方程为•试确定系统可观测时应满足的条件。iic,xccccyu2010x11x43212211解:x2010yuccccx1010x43212211由对偶系统的可控性判据可知,其可控的充要条件为.0c,0c,3121这也就是原系统可观测的条件。构造原系统的对偶系统如下:4可观测标准形•一个单输出系统如果其A,c阵有如下的标准形式,它一定是可观测的。(9-122)式称为单输出系统的可观测标准形。0121000010001000001000001nAc(9-122)xcy,ubxAx通过对偶原理证明:•给定系统方程如下cxy,buAxx)xMx(xMx1(9-123)•若有等价变换•将其化为可观测标准形式中具有(9-122)的形式。Ac和构造原系统的对偶系统根据对偶原理,因原系统为可观测,所以其对偶系统一定可控。zbw,uczAzTTTPzz化为下列的可控标准形,其变换矩阵为P.zcw,ubzAz11111111PbcPcbPPAATTT,,因此有TT11TT1T1TT1cPbb)P(cAP)P(AcMcbMbAMMA11TPM(9-134)比较上面两组式子,可知欲求之线性变换矩阵它可将系统方程化为可观测标准形。例9-17•系统动态方程为•将系统动态方程化为可观标准形,并求出变换矩阵。x11y,u11x1111x解:•显然该系统可观测,可以化为可观标准形。写出它的对偶系统的A,b阵,分别为11b,1111A•根据A,b阵,按化可控标准形求变换阵的步骤求出P阵:•计算可控性矩阵S0121AbbS5.05.0h5.05.0100121S11015.05.0hAhP•由(9-128)式求出P阵1120M,05.015.0015.05.0PM1TT•由(1-60)式求出M阵•式中1005.015.011cMc02111120bMb212005.015.011111120AMMA115系统按可观性进行分解•系统可观测,则通过等价变换可以化为可观测标准形。现在研究系统不可观的情况,它是系统不可控的对偶结果。若(9-113,114)的系统不可观测,且nncAcAcrank21n则存在可逆矩阵P,将动态方程化为式中是n2维向量,是n-n2维向量,并且1x2xnnAcAccrank21n111112(9-137)211212143121xx0cyubbxxAA0Axx(9-135)(9-136)(9-135,136)的式子也可用图9-14表示。•这可以用前面证明可观标准形的方法论证。(9-137)式表明n2维的子系统(A1b1c1)是可观的;这部分状态变量是不可观的;(9-138)式表明传递函数未能反映系统的不可观部分。2x11111)()(1bAsIcbAsIcn•系统按可观性分解的结果(9-138)图9—14系统按可观测性分解由图上可以看出传递函数完全由图中虚线以上的部分所决定,即传递函数未能反映系统中不可观测的部分。四、可控性、可观测性与传递函数的关系)s(D)s(NAsIb)AsI(cadjb)AsI(c)s(g1(9-141)对应的传递函数为cxy,buAxx(9-140)考虑单变量系统,其动态方程为1、可控性、可观测性与零、极点对消问题式中:AsI)s(Db)AsI(cadj)s(NN(s)=0的根称为传递函数g(s)的零点,D(s)=0的根称为传递函数g(s)的极点。下面是本段的主要结果。定理定理动态方程式(9-140)可控、可观测的充分必要条件是g(s)无零、极点对消,即D(s)和N(s)无非常数的公因式。证明:首先用反证法证明条件的必要性,若有s=s0既使N(s0)=0,又使D(s0)=0,由(9-141)式即得0b)AIs(cadj,0AIs00(9-143)利用恒等式IAsIb)AsI(cadj)AsI()AsI)(AsI(1I)s(D)AsI(adj)AsI(可得(9-144)将s=s0代入(9-144)式,并利用(9-143)式,可得)AIs(Aadj)AIs(adjs000(9-145)将上式前乘c、后乘b后即有0)s(Nsb)AIs(cadjsb)AIs(cAadj00000(9-146)将(9-145)式前乘cA、后乘b后即有0b)AIs(cAadjsb)AIs(adjcA0002(9-147)依次类推可得0b)AIs(adjcA0b)AIs(adjcA0b)AIs(cAadj0b)AIs(cadj)s(N01n0200这组式子又可写成0b)AIs(adjcAcAc01n出现矛盾,矛盾表明N(s)和D(s)无相同因子,即g(s)不不会会出现零、极点相消的现象。因为动态方程可观测,故上式中前面的可观性矩阵是可逆矩阵,故有0b)AIs(adj00ss1b)AIs(adj1n000又由于系统可控,不妨假定A、b具有可控标准形(9-92)的形式,直接计算可知(9-148)例9-18•设系统动态方程为101010146411210xxuyx•不难验证系统是可控、可观测的。•显然N(s)和D(s)无非常数的公因式,这时传递函数没有零、极点相消。事实上422342)1s()1s(1s4s6s4s1s2s)s(g1s4s6s4sAsI)s(D1s2sb)AsI(cadj)s(N2342•分别计算2传递函数的最小阶动态方程实现已知动态方程,可以用(9-64)式计算出传递函数。如果给出传递函数如何找出它所对应的动态方程?这一问题称为传递函数的实现问题。如果又要求所找出的动态方程阶数最低,就称为传递函数的最小实现问题。设给定有理函数011n1nn011n1n011n1nn011n1nn0asasasbsbsbdasasasdsdsdds)s(g(9-149)(9-149)式中的d就是下列动态方程中的直接传递部分ducxy,buAxx(9-150)所以只需讨论(9-149)式中的严格真有理分式部分。给定严格真有理函数011n1nn011n1nasasasbsbsb)s(g(9-151)要求寻找A,b,c,使得)s(gb)AsI(c1(9-152)并且在所有满足(9-152)式的A,b,c中,要求A的维数尽可能的小。下面分两种情况讨论①可控标准形的最小阶实现式(9-153)对(9-151)式,可构造出如下的实现(A,b,c)1n101n210bbbc1000b1000001000010A(9-153)(1)g(s)的分子和分母无非常数公因式的情况1000cbbbb10001001000A1n101n210(9-154)②可观标准形的最小阶实现(9-153)式给出的(A,b,c)具有可控标准形,故一定是可控的。可直接计算它对应的传递函数就是(9-151)的传递函数。由于g(s)无零、极点对消,故可知(9-153)式对应的动态方程也一定可观。同样可以说明(9-154)式是(9-151)的可观标准形的最小实现。若g(s)的分母已经分解成一次因式的乘积,通过部分分式分解,容易得到约当标准形的最小阶实现。现用例子说明,设g(s)有以下的形式)s(c)s(c)s(c)s(c)s()s(bsbsbsb)s(g)s(u)s(y4413212311431012233(9-155)③约当标准形的最小阶实现因为g(s)无零、极点对消,故可知上式中c1c4均不为零。令)s(us1)s(x)s(xs1)s(u)s(1)s(x)s(xs1)s(u)s(1)s(x)s(us1)s(x44213113121213uxxxxxxxxuxx44421113212313分别对应于而44332211xcxcxcxcy综合上面各式并令x=[x1x2x3x4]T可得xccccyu1100x001001x43214111由若当形方程的可控性判据和可观测性判据可知上式是可控、可观测的,因而它是g(s)一个最小阶实现。若g(s)的分母是n阶多项式,但分子和分母有相消的公因式时,这时n阶的动态方程实现就不是最小阶实现,而是非最小实现,(或是不可控的,或是不可观的,或是既不可控也不可观的)。g(s)的最小实现的维数一定小于n。(2)g(s)的分子和分母有相消因式的情况例9-19设g(s)的分子N(s)=s+1,而分母D(s)=,分子与分母有公因子(s+1)。1s2s2s23仿照(9-153)式,可写出g(s)的一个三维的可控标准形实现x011yu100x221100010x无须验证这个实现是可控的x100yu011x210201100x因此这一实现是不可观的。同理,如果按(9-154)式构造如下的可观测标准形的三维实现,它一定是不可控的。2rankV121110011V计算可观测性矩阵当然也可以构造出g(s)的既不可控又不可观测的三维实现。现在将分子和分母中的公因式消去,可得1ss11s2s2s1s)s(g223如果用上式中最后的式子,仿照(9-153)式或(9-154)式,构造出二维的动态方程实现,它是g(s)的最小实现。9-3状态反馈与状态观测器本节首先研究用状态变量作反馈的控制方式。系统的动态方程如下cxy,buAxx(9-157)令kxvu(9-158)一、状态反馈和极点配置问题式中的v是参考输入,k称为状态反馈增益矩阵,这里它是1×n的向量。返回子目录图9-15cxy,bvx)bkA(x(9-159)图9-15所示的闭环系统的状态空间表达式为式中A-bk为闭环系统的系统矩阵。•将(9-157)式和(9-158)式用方框图表示,见图9-15,它是一个闭环系统。计算(9-159)式闭环系统的可控性矩阵,因为)bA,,bA,Ab,b(bAb)bkA()bA,Ab,b(bA))Ab,b(bA)(bkA(b)bkA()Ab,b(bA)bdAb)(bkA(b)bkA(bdAbbkbAbb)bkA(2n21n1n232322的线性组合的线性组合的线性组合的线性组合1状态反馈不影响可控性10000101bAAbbb)bkA(b)bkA(b1n1n上式中最后一个矩阵显然是非奇异矩阵,因此有bAAbbrank]b)bkA(b)bkA(b[rank1n1n(9-160)因此有式(9-160)表明,若原来系统可控,加上任意的状态反馈后,所得到的闭环系统也可控。若原来系统不可控,不论用什么k阵作状态反馈,所得到的闭环系统仍然不可控。这一性质称为状态反馈不改变系统状态反馈不改变系统的可控性。的可控性。状态反馈可能改变系统的可观测性。即原来可观的系统在某些状态反馈下,闭环可以是不可观的。同样,原来不可观的系统在某些状态反馈下,闭环可以是可观的。状态反馈是否改变系统的可观测性,要进行具体分析。例9-20•系统的动态方程如下xccy,u10x1011x21下表列出了系统c阵参数、状态增益向量k和系统可观测性的关系。可观任意可观01可观[11]11不可观[12]可观11不可观[01]10可观[11]不可观10闭环系统k原系统c2c1可观性的变化可以从闭环传递函数的极点变化、是否发生零极点对消来说明。2状态反馈对闭环特征值的影响闭环方程(9-159)中的系统矩阵A-bk的特征值,一般称为闭环的极点。闭环系统的品质主要由闭环的极点所决定,而稳定性则完全由闭环极点所决定。通过选取反馈增益阵来改变闭环特征值在复平面上的位置,称为状态反馈进行极点配置问题。证明:定理:闭环方程(9-159)的系统矩阵A-bk的特征值可以由状态反馈增益阵k配置到复平面的任意位置,其充分必要条件是(9-157)式的系统可控。先证充分性因为(9-157)式的系统可控,则存在可逆矩阵P,将(9-157)式的系统通过的变换化为可控标准形。Pxx1n101n10cccc100baaa1010AxcyubxAx式中(9-161)现引入1n10kkkk(9-162)这时(9-158)式的状态反馈式可写为:考虑矩阵xkvxkPvkxvu1PkkkPk1)ka()ka()ka(1110kbA1n1n1100它的特征式为由于)]kbA(sIdet[)ka(s)ka(s)ka(s00111n1n1nn)]PbkPPAP(sIdet[)]kbA(sIdet[11)]bkA(sIdet[}P)]kbA(sI[Pdet{1故的特征式即是的特征式,所以和有相同的特征值。bkAkbAbkAkbA设任意给定的闭环极点为,且n21,,,011n1nnn21sss)s()s)(s((9-166)式中完全由所决定。比较(9-165a)式和(9-166)式可知,若要(9-166)的根为,需有)1n,,2,1i(iiiiiiiiiak)1n,,1,0i(ka(9-167)这说明任意给定闭环n个极点,均可通过(9-167)、(9-163)式确定,使A-bk具有给定的n个特征值,充分性证毕。必要性若系统(9-157)可任意配置闭环特征值,要证明系统(9-157)可控。用反证法,若系统(9-157)不可控,则存在一个可逆矩阵,通过等价变换后,可将(9-157)式转换为(9-104,105)的可控分解形式。考虑矩阵4212111211421A0kbAkbAkk0bA0AAkbAkA4的特征值不受的影响,即A-bk中的一部分特征值不受k的影响,这与可任意配置A-bk的特征值相矛盾。矛盾表明系统(9-157)可控。以上定理的充分性证明中,已给出通过可控标准形来选择k阵,使闭环具有任意要求的特征值的计算步骤,现归纳如下①计算A的特征式011n1nnasasas)AsIdet(②由所给的n个期望特征值,计算期望的多项式n21,,,011n1nnn21sss)s()s)(s(④根据(9-94)式,计算化可控标准形的坐标变换阵PPkk⑤求出反馈增益阵上述步骤中有化可控标准形这一步。如果不经过这步,也可直接求k。)aaa(k1n1n1100③求ku1010x01100100001000010x系统状态方程为若加状态反馈使闭环特征值分布为{-1,-2,-1+j,-1-j},试求状态反馈增益阵k。例9-21方法一、通过化可控标准形求解242211)11()det(ssssAsI①计算A的特征式②由所给的4个期望特征值,计算期望的多项式4s10s10s5s)2s2s)(2s)(1s(2342解:⑤求出反馈增益阵100001001.01.0001.001.0PPkk=[-0.4-1-21.4-6]④根据(9-94)式,计算化可控标准形的坐标变换阵P③求521104]05111001004[k方法二:令,计算A-bk的特征式4321kkkkk432241321()(11)1010sIAbkskkskksksk比较两个特征式的系数可得4k10,10k10,1011kk,5kk123142所以可得k=[-0.4-1-21.4-6]最后强调:在极点配置定理中,“任意配置”是和系统可控等价的。若不要求任意配置,就不一定要求系统可控。因此给定一组期望的特征值,只有它包含了所有不可控部分的特征值时,才是可配置的。例9-22•设系统状态方程为•这一系统是不可控的。uxx11101000010000200012•若指定闭环特征值{-2,-2,-1,-1},{-2,-2,-2,-1}1100010000100001P11000100001000011P10000100002000121PAP0110Pb0210kkkk令有100001020012210210kkkkkkkbA20112)2(42)4(skksks441k44201kk所以00816k00816Pkk02k令对{-2,-2,-2,-1}100001020012210210kkkkkkkbA)(kbAsI)1](442)4()3([2102102213skkkskkkskks)1()2(3ss84421246321021021kkkkkkkk所以有•但若指定闭环特征值为{-2,-2,-2,-2},•就找不出k来达到这一配置要求。091980364k091980364Pkk例9-23)2s)(1s(s10)s(u)s(y有一系统的传递函数为要求用状态反馈的方法,使得闭环系统的特征值为-2,-1+j,-1-j。解:首先要将系统用状态方程写出,即构造出传递函数的实现,为了计算方便,取可控标准形实现x0010yu100x3201010x反馈增益向量k可写成210kkkk闭环系统的特征方程为0ks)k2(s)k3(s01223状态反馈系统的方框图如图9-16所示。按给定极点,期望多项式为4s6s4s)j1s)(j1s)(2s(23比较上两特征多项式,令s同次的系数相等,可得1k4k4k210或k=[441]图9-16例9-23在引入状态反馈后的结构图二、状态观测器为了实现状态反馈,须对状态变量进行测量,但在实际系统中,并不是所有的状态变量都能测量到的。因此为了实现状态反馈控制律,就要设法利用巳知的信息(输入量及输出量),通过一个模型来对状态变量进行估计。状态观测器又称状态渐近估计器。图9-17状态的开环估计一个明显的方法是利用计算机构成一个与实际系统具有同样动态方程的模型系统,用模型系统的状态变量作为系统状态变量的估计值,见图。由于图9-17中未能利用系统的输出信息对误差进行校正,所以用图9-17得到的估计值是一个开环估值。一般系统的输入量u和输出量y均为已知,因此希望利用y=cx与的偏差信号来修正的值,这样就形成了图9-18的闭环估计方案。xˆcyˆxˆ图9-18状态的闭环估计方案根据图9-18所表示的关系可写出观测器部分的状态方程Hybuxˆ)HcA()xˆcy(HbuxˆAxˆ(9-169)由(9-169)式和系统方程式可求出观测误差应满足的方程式xˆxx~x~)HcA()xˆx)(HcA()xxˆ(Hc)xˆx(A]Hcxbuxˆ)HcA[(buAxxˆxx~(9-170)(9-170)式表明,只要A-Hc的特征值均在复平面的左半部,随着t的增长而趋向于零,而且趋于零的速度由A-Hc的特征值所决定。于是有下面极点可任意设置的状态观测器定理x~定理:若系统(Abc)可观测,则(9-169)式给出了系统的一个n维状态观测器,并且观测器的极点可以任意配置。例9-24•系统的动态方程为试设计一个状态观测器,观测器的特征值要求设置在{-10,-10}。x02yu10x3210x解:将观测器增益矩阵H写成0h20h202hhHc,hhH212121观测器的特征方程为0)2h2h6(s)3h2(s3sh221h2s)HcA(sI211221根据给定的特征值,可求出期望的多项式为100s20s)10s(22比较上述两多项式中s的同次项系数得5.23h,5.8h21因此观测器的方程为y5.235.8u10xˆ349117xˆ三、由被控对象、观测器和状态反馈构成的闭环系统若原系统(对象)方程为cxy,buAxx(9-171)现以状态观测器所得到的状态估计值代替原系统的状态变量x形成状态反馈,即xˆxˆkvu(9-172)而观测器的方程为Hybuxˆ)HcA(xˆ(9-173)由对象、观测器和状态反馈组合而成的闭环系统的方框图如图9-19所示。图9-19带观测器的状态反馈系统将(9-172)式代入(9-171)式和(9-173)式,可分别得到buHcxxˆ)bkHcA(xˆcxy,bvxˆbkAxx(9-174)(9-175)TTT]xˆx[取状态变量为xˆx0cyvbbxˆxbkHcAHcbkAxˆx(9-176)(9-177)将(9-176)、(9-177)式的动态方程进行如下的坐标变换xˆxII0Ix~x(9-178)II0IPII0IP1所得到的动态方程为:x~x0cyv0bx~xHcA0bkbkAx~x(9-179)(9-180)b)]bkA(sI[c)s(g1f闭环系统的传递函数可以通过(9-179)式、(9-180)式来计算。从(9-179)式可知,这时闭环系统矩阵的特征式可计算如下)]HcA(sIdet[)]bkA(sIdet[HcA0bkbkAsIdetnnn2(9-181)上式表明,图9-19所示闭环系统的特征式等于矩阵A-bk与矩阵A-Hc的特征式的乘积,而A-bk是状态反馈系统的系统矩阵,A-Hc是观测器的系统矩阵,(9-181)式表明状态反馈系统的动态特性和观测器的动态特性是相互独立的。这个特点表明:若系统是可控、可观的,则可按闭环极点配置的需要选择反馈增益阵k,然后按观测器的动态要求选择H,H的选择并不影响已配置好的闭环传递函数的极点。因此系统的极点配置和观测器的设计可分开进行,这个原理通常称为分离定理。通常把反馈增益阵和观测器一起称为控制器图9-20控制器例9-25•设系统传递函数为希望用状态反馈使闭环的极点为-4±6j,并求实现这个反馈的状态观测器,观测器的极点设置在-10,-10。)6s(s1)s(G解:由系统的传递函数可知,其二阶动态方程实现是可控且可观的。为了设计观测器方便,现取可观标准形实现,即x10yu01x6100x根据题意要求闭环特征方程为052s8s2122hs)h6(s)HcA(sI令两个特征式对应的系数相等,可解出k1=2,k2=40。再求观测器,根据极点的要求,期望多项式为0100s20s2令,使T21hhH求状态反馈k,令k=[k1k2]。求出状态反馈后闭环系统的特征多项式1212k6ks)k6(s)bkA(sI与期望多项式相比,得到h1=100,h2=14。由式可计算出观测器方程为y14100u01x2011000xˆ由对象、状态反馈和观测器构成的整个闭环系统的方框图如图9-21所示。图9-21例9-25的反馈控制系统dBuetxttA)()(0)((9-183)它在零初始条件的输出§9-4有界输入、有界输出稳定性设系统的动态方程为CxyBuAxx(9-182)bcetgAt令dutgtxt)()(0(9-184)则有式中g(t)为脉冲响应函数。返回子目录传递函数与脉冲响应函数的关系为bAsIcsG1bAsIcbceLAt1定义Kth,0t若对于成立,称h(t)有界。系统BIBO稳定的充分必要条件为K是一个实的正数。0Kdttg(9-187)若所有的有界输入引起的零状态响应的输出是有界的,则称系统为有界输入有界输出稳定,即BIBO稳定。证明:充分性1)(ktuttdutgdutgty00)()()()()(ttdttgkdutg01110)()()(Kk1设必要性反证法若有存在,使得1t10)(tMdttgM>0)]([)(1tgsignu],0[1t取有界输入1100111)()()()(ttdtgdutgty这时令1t101)()(tMdgty当系统用传递函数描述时,系统BIBO稳定的充分必要条件为g(s)的极点具有负实部。若式(9-182)中的A阵,其特征值均在复平面的左半部,称动态方程是渐近稳定的。例9-26•分析下列系统的输入、输出稳定性和渐近稳定性。xyuxx10121160解:系统的特征方程为det()(1)6(3)(2)0sIAssss系统传递函数31)()(1sbAsIcsG传递函数极点位于S左半平面,故系统是输入、输出稳定的。A阵的特征值为+2,-3。故系统不是渐近稳定的。结论:•若系统(A,b,c)是渐近稳定的,则也是输入、输出稳定的;•若系统(A,b,c)是输入、输出稳定的,且又是可控和可观的,则系统是渐近稳定的。渐近稳定BIBO稳定9-5李雅普诺夫第二方法李雅普诺夫第二方法是通过构造李雅普诺夫函数(V函数)来直接判断运动稳定性的一种定性的方法.由于这种方法没有求出微分方程的解,而直接研究方程解的稳定性,因此又称为直接法,目前它仍然是研究系统(包括时变、非线性)稳定性的有力工具。这里只针对时不变线性系统渐近稳定的情况介绍二次型形式的V函数。返回子目录定理:•时不变动态方程的零解是渐近稳定的充分必要条件是对给定的任一个正定对称阵N,都存在唯一的正定对称阵M,使得Axx(9-188)式的矩阵方程称为李雅普诺夫方程。NMAMAT(9-188)例9-27•考虑二维系统•试确定平衡状态x=0是否渐近稳定。2121xx1110xx解:令N=1,M由(9-188)式来确定。设代入(9-188)式,可以得到4221mmmmM10011110mmmmmmmm1110422142211mmmmM2121234221显然M是正定矩阵。所以系统的平衡状态x=0渐近稳定。例9-28•考虑二维系统•试确定平衡状态x=0渐近稳定时待定参数a应满足的条件。a≠02121xx1a10xx解:令N=1,M由(9-188)式来确定。设4221mmmmM10011a10mmmmmmmm11a042214221代入(9-188)式,可以得到解出2122411221122aammaaMmmaaa由于二次三项式大于零,故由得a>0,这时也大于零,即M阵正定的条件为a>0,这也就得到了系统渐近稳定时,A中的待定参数a应满足的条件:a>0。21aa10m2142mmm定理并不意味着“A渐近稳定,M正定,由(9—188)式所得的N一定正定。”注意例9-29•设5221M,3111A•显然A的特征值均有负实部,M正定,但按式(9—188)计算出的却不是正定的26222N由上述定理可知若渐近稳定,一定存在正定二次型作为它的李雅普诺夫函数,并且是负定二次型,这一事实的几何意义可说明如下。()TVxxMxAxxTxNx可认为通过V函数给状态空间的点赋予了一个正数,于是可把V函数看作状态空间到原点距离的一种度量。•取一正的数列:且。考察曲面),2,1k(CMxx:SkTknC,CCCk210Climkk•的非零解x(t)在状态空间中表示一条曲线,称为轨线。V(x)沿这些曲线的导数另外从几何上看AxxAxx)x(vxxxx)x(vx)x(vx)x(vxx)x(vdt)x(dvTn21n21n1ii0NxxMAxxMxAxxMxMxxTTTTTT•上式中的,即表示那些椭球面的外法向,而Ax表示了轨线的方向,•表明椭球面的外法向和轨线方向的夹角为钝角,即轨线应由外向里穿过层层的椭球面,最终趋向于原点。xv)x(gradv0Ax)xv(T本章主要知识点及线索不可观可观不可控可控状态空间模型(A、b、c、d)状态方程的解可控标准形对偶原理可观标准形状态反馈可任意配置极点分离定理可控性判据可控性分解可观性判据可观子系统可控标准形实现可观性分解可观标准形实现n维状态观测器可任意配置观测器极点传递函数teA可控子系统对象、观测器、状态反馈组成闭合系统•345额

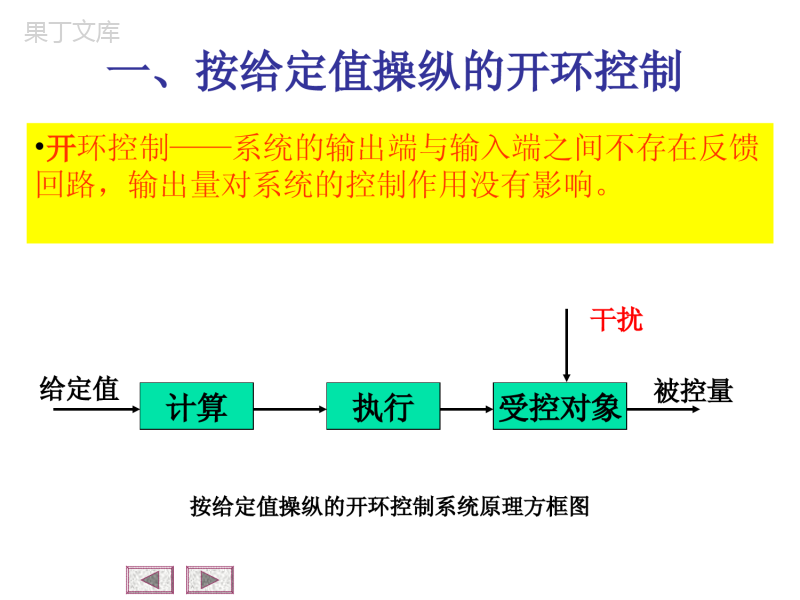
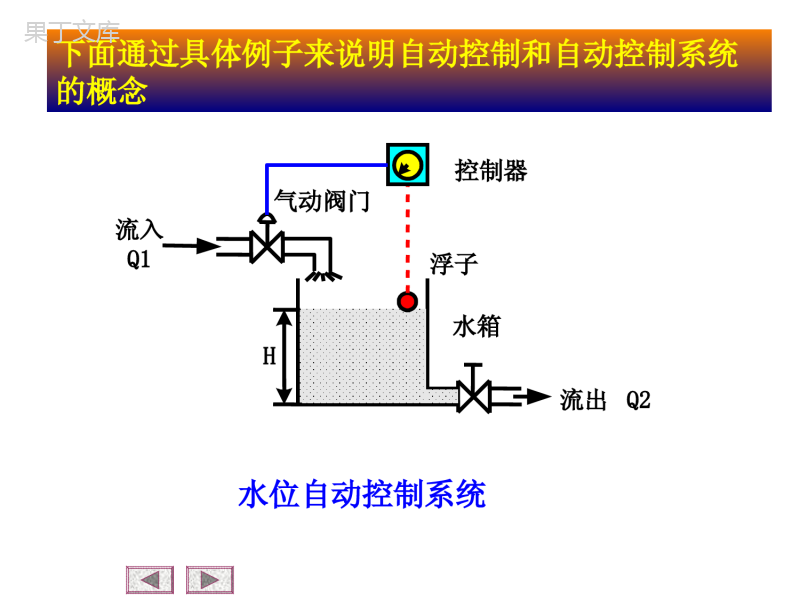
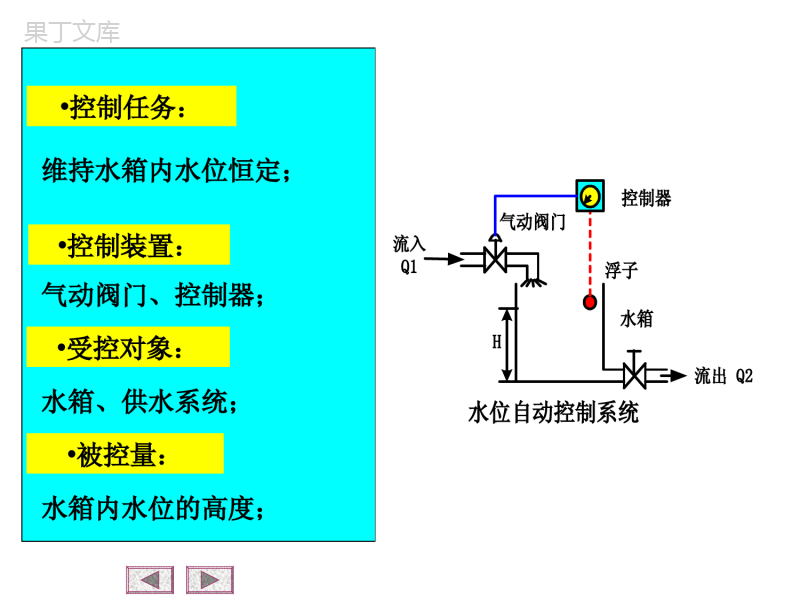

 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载