确定二次函数的表达式-2022-2023学年九年级数学下册同步精品课件(北师大版)

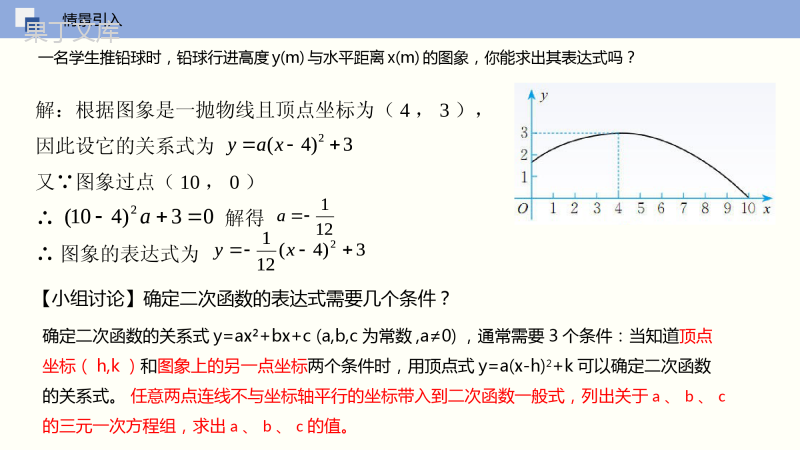
数学（北师大版）九年级下册2.3确定二次函数的表达式第二章二次函数课前导入学习目标1、通过待定系数法求二次函数的关系式。2、根据实际问题的不同条件建立相应的二次函数关系式。重点用待定系数法求二次函数的关系式。难点根据实际问题的不同条件建立相应的二次函数关系式。知识点回顾我们在用待定系数法确定一次函数y=kx+b(k,b为常数，k≠0)的关系式时，通常需要个的条件.确定反比例函数y=（k≠0)关系式时，通常需要个条件.21如果确定二次函数y=ax2+bx+c(a,b,c为常数，a≠0）的关系式时，通常又需要几个条件？解：根据图象是一抛物线且顶点坐标为（4，3），因此设它的关系式为又∵图象过点（10，0）∴解得∴图象的表达式为情景引入一名学生推铅球时，铅球行进高度y(m)与水平距离x(m)的图象，你能求出其表达式吗？3)4(2xay03)410(2a121a3)4(1212xy【小组讨论】确定二次函数的表达式需要几个条件？确定二次函数的关系式y=ax²+bx+c(a,b,c为常数,a≠0)，通常需要3个条件：当知道顶点坐标（h,k）和图象上的另一点坐标两个条件时，用顶点式y=a(x-h)2+k可以确定二次函数的关系式。任意两点连线不与坐标轴平行的坐标带入到二次函数一般式，列出关于a、b、c的三元一次方程组，求出a、b、c的值。3)4(2xay03)410(2a121a3)4(1212xy课堂基础练已知二次函数y=ax2+c的图象经过点（2，3）和（－1，－3），求出这个二次函数的表达式.解：将点（2，3）和（－1，－3）分别代入二次函数y=ax2+c中，得3=4a+c,-3=a+c,解这个方程组，得a=2,c=-5∴所求二次函数表达式为：y=2x2－5.课堂基础练若二次函数经过(-1,10)、(1,4)、(2,7)三个点，能求出二次函数的解析式吗？解得a=2，b=-3，c=5，所以二次函数为设二次函数为?−?+?=10?+?+?=44?+2?+?=7课堂基础练已知二次函数图象的顶点为（3，-4），与y轴的交点为（0，2），求这个二次函数的解析式.解：设所求二次函数为y=ax2+bx+c.由已知，与y轴的交点为（0，2），得c=2.由已知，顶点为（3，-4），得23244.4baacba,23244.4baacba,课堂基础练解：设所求二次函数为由已知，顶点为（3，-4），则二次函数为2()yaxhk由已知，与y轴的交点为（0，2），得22(03)4a，所求二次函数为22(3)4.3yx已知二次函数图象的顶点为（3，-4），与y轴的交点为（0，2），求这个二次函数的解析式.2()yaxhk22(03)4a，22(3)4.3yx课堂基础练已知抛物线图象上三个点的坐标（1，0），（3，0），（2，-1），求二次函数关系式。解法一:设所求二次函数关系式为：y=ax2+bx+c.又抛物线过点（1，0），（3，0），（2，-1），依题意得:a+b+c=09a+3b+c=04a+2b+c=-1解得1a4b3c∴所求的函数关系式为。243yxx1a4b3c243yxx课堂基础练解法二∵点（1，0）和（3，0）是抛物线与x轴的两个交点，∴设二次函数关系式为：y=a(x-1)(x-3),又抛物线过点（2，-1），∴-1=a（2-1)（2-3）解得∴即所求的函数关系式为。已知抛物线图象上三个点的坐标（1，0），（3，0），（2，-1），求二次函数关系式。随堂测试1一个二次函数，当x＝0时，y＝﹣5；当x＝﹣1时，y＝﹣4；当x＝﹣2时，y＝5，则这个二次函数的关系式是（）A．y＝4x2+3x5﹣B．y＝2x2+x+5C．y＝2x2x+5﹣D．y＝2x2+x5﹣【详解】解：设二次函数的关系式是y＝ax2+bx+c（a≠0），∵当x＝0时，y＝﹣5；当x＝﹣1时，y＝﹣4；当x＝﹣2时，y＝5，∴c＝﹣5①，a﹣b+c＝﹣4②，4a2﹣b+c＝5③，解由①②③组成的方程组得，a＝4，b＝3，c＝﹣5，所以二次函数的关系式为：y＝4x2+3x5﹣．故选：A．随堂测试2已知抛物线经过点(0，-2)，(3，0)，(-1，0)，求抛物线的解析式．【详解】∵抛物线经过点(3，0)，(-1，0)，故可设该抛物线的解析式为：，∵该抛物线又经过点(0，-2)，∴解得：∴该抛物线的解析式为：整理，得：．随堂测试x-1012y01.521.53．二次函数y=ax2+bx+c(a≠0)的x、y的部分对应值如下表所示，则下列判断不正确的是（）A．当x＜0时，y随x的增大而增大B．当时，y=-2C．顶点坐标为(1，2)D．是方程的一个根【详解】解：由题意得：，解得，∴二次函数y=ax2+bx+c的解析式为y=-x2+x+=-（x-1）2+2，∴顶点坐标为(1，2)，选项C不符合题意；∵-开口向下，∴x＜1时，y随x的增大而增大，∴x＜0时，y随x的增大而增大，选项A不符合题意；当x=4时，y=-2.5，选项B符合题意；∵x=-1时，y=0，∴x=-1是方程的一个根，选项D不符合题意；故选：B．课后总结如何选择不同形式的二次函数的关系式？1．一般式（已知抛物线上三点或三对x、y的值，用一般式.）2．顶点式：（已知抛物线的顶点或对称轴或最值，用顶点式.）3．交点式：（已知抛物线与x轴两交点的坐标，用交点式。）2(0)yaxbxca2(a0)yaxhk12()()(a0)yaxxxx2(0)yaxbxca2(a0)yaxhk12()()(a0)yaxxxx谢谢~