《立体几何中的向量方法》人教版高中数学选修2-1PPT课件（第1课时）.pptx

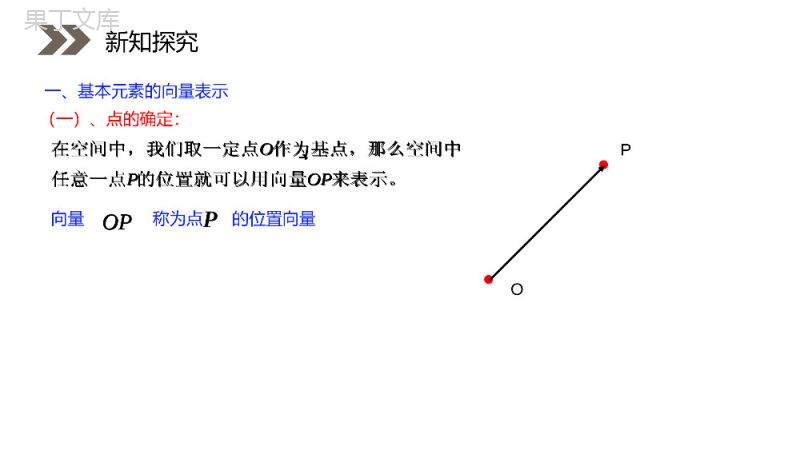
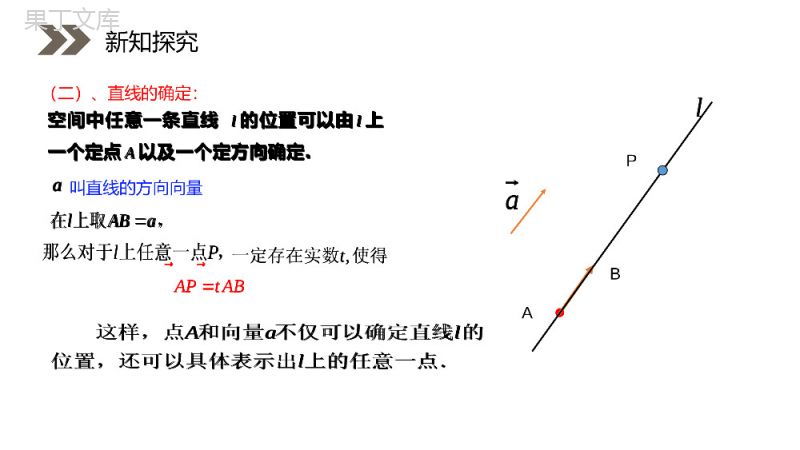
人教版高中数学选修2-1讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-13.2立体几何中的向量方法第一课时第3章空间向量与立体几何平面向量空间向量推广到立体几何问题研究课前导入平面向量空间向量推广到立体几何问题2、如何确定一个点、一条直线、一个平面在空间的位置？1、构成空间图形的基本元素：点、直线、平面新知探究OPOP在空间中，我们取一定点作为基点，那么空间中任意一点的位置就可以用向量来表示。OP（一）、点的确定：向量称为点的位置向量OPP一、基本元素的向量表示新知探究OPOP在空间中，我们取一定点作为基点，那么空间中任意一点的位置就可以用向量来表示。OPPaAB（二）、直线的确定：空间中任意一条直线l的位置可以由l上一个定点A以及一个定方向确定.la叫直线的方向向量lP那么对于上任意一点，Aall这样，点和向量不仅可以确定直线的位置，还可以具体表示出上的任意一点．lABa在上取，,APtABt一定存在实数使得P新知探究a空间中任意一条直线l的位置可以由l上一个定点A以及一个定方向确定.lalP那么对于上任意一点，Aall这样，点和向量不仅可以确定直线的位置，还可以具体表示出上的任意一点．lABa在上取，,APtABt一定存在实数使得空间中平面的位置可以由内两条相交直线来确定．Oab如图,设这两条直线相交于点,其方向向量分别为和，P为平面上任意一点，(,),.xyOPxayb由平面向量基本定理知，存在有序实数对使Oab这样,点与向量，不仅可以确定平面的位置，还可以具体表示出内的任意一点,这种表示在解决几何问题时有十分重要的作用．ab·P（三）、平面的确定：Oab1、点与向量，新知探究空间中平面的位置可以由内两条相交直线来确定．Oab如图,设这两条直线相交于点,其方向向量分别为和，P为平面上任意一点，(,),.xyOPxayb由平面向量基本定理知，存在有序实数对使Oab这样,点与向量，不仅可以确定平面的位置，还可以具体表示出内的任意一点,这种表示在解决几何问题时有十分重要的作用．Oab1、点与向量，如果表示向量的有向线段所在直线垂直于平面，则称这个向量垂直于平面,记作⊥，如果⊥，那么向量叫做平面的法向量.nnnnnl2、平面的法向量：2.一个平面的所有法向量都互相平行;注意：1.法向量一定是非零向量;新知探究nnnnnn3、给定一点A和一个向量,那么过点A,以向量为法向量的平面是完全确定的.nnA新知探究nnn二、基本元素间位置关系的向量表示（一）、两条直线：,,lmabrr设直线的方向向量分别为////.lmabakbkRrrrr0lmababrrrrgmbrlarlarmbr线线平行线线垂直新知探究,,lmabrr设直线的方向向量分别为////.lmabakbkRrrrr0lmababrrrrgmbrlarlarmbrua（二）、直线与平面：l,laurr设直线的方向向量为平面的法向量为//0lauaurrrrg//.lauakukRrrrrual线面平行线面垂直新知探究ual,laurr设直线的方向向量为平面的法向量为//0lauaurrrrg//.lauakukRrrrrual设平面,的法向量分别为,uv，∥u∥v.ukvuv（三）、两个平面：⊥u⊥v.0vuuv面面平行面面垂直新知探究设平面,的法向量分别为,uv，∥u∥v.ukvuv⊥u⊥v.0vuuv,,,//,//lmlmlmlm直线和平面，其中，与相交，已知：．//求证：．,,,,hlmpabp在内任取一条直线，设的方向向量分证明别为：，,,,,,.lmlmxypxayb且相交存在实数，使例1.证明平面和平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行,则这两个平面平行．例题讲解,,,//,//lmlmlmlm直线和平面，其中，与相交，已知：．//求证：．,,,,hlmpabp在内任取一条直线，设的方向向量分证明别为：，,,,,,.lmlmxypxayb且相交存在实数，使,,,//,//,,0,0,uvlmavbvavbv设的法向量分别为，()0,//,//.pvxaybvxavybvvvuv的法向量与内的任一直线垂直，也是的法向量，pxayb，例1.证明平面和平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行,则这两个平面平行．例题讲解,,,//,//,,0,0,uvlmavbvavbv设的法向量分别为，()0,//,//.pvxaybvxavybvvvuv的法向量与内的任一直线垂直，也是的法向量，pxayb，直线a，b的方向向量分别为a＝(1，－1,2)，b＝(－2,2，－4)，则()A．a∥b或a与b重合B．a⊥bC．a与b相交但不垂直D．a与b异面但不垂直解析：∵a＝(1，－1,2)，b＝(－2,2，－4)，∴b＝－2a，∴a与b共线．即a∥b或a与b重合．A巩固训练,,//lmlmlm直线和平面，其中，已知：．//l求证：．,,lmabu设的方向向量分别为，平面的法向：量证明．//(),lmakbkR，练习：证明直线和平面平行的判定定理：平面外一条直线与这个平面内的一条直线平行,则该直线与这个平面平行．,,,0,umubub()0,//.uaukbl巩固训练,,//lmlmlm直线和平面，其中，已知：．//l求证：．,,lmabu设的方向向量分别为，平面的法向：量证明．//(),lmakbkR，,,,0,umubub()0,//.uaukbl,,.lll直线和平面，其中且已知：求证：．,,lauv设直线的方向向量为平面的法证向量分别为，明：．,//,(),lauukakR练习：证明平面和平面垂直的判定定理：一个平面经过另一个平面的垂线，则这两个平面垂直．,0,()0,lavuvkav于是．巩固训练,,.lll直线和平面，其中且已知：求证：．,,lauv设直线的方向向量为平面的法证向量分别为，明：．,//,(),lauukakR,0,()0,lavuvkav于是．,,lmabuv设直线的方向向量分别为，，平面的法向量分别为，，则有////()lmabakbkR线线平行：//0lauau线面平行：////()uvukvkR面面平行：1.空间平行关系的向量表示：线线平行包括线线重合，线面平行包括线在面内，面面平行包括面面重合．注意：课时小结,,lmabuv设直线的方向向量分别为，，平面的法向量分别为，，则有////()lmabakbkR线线平行：//0lauau线面平行：////()uvukvkR面面平行：线线平行包括线线重合，线面平行包括线在面内，面面平行包括面面重合．注意：,,lmabuv设直线的方向向量分别为，，平面的法向量分别为，，则有0lmabab线线垂直：//()lauakukR线面垂直：0uvuv面面垂直：2.空间垂直关系的向量表示：课时小结,,lmabuv设直线的方向向量分别为，，平面的法向量分别为，，则有0lmabab线线垂直：//()lauakukR线面垂直：0uvuv面面垂直：感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明人教版高中数学选修2-1讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-1感谢你的聆听第3章空间向量与立体几何