《微积分基本定理》人教版高中数学选修2-2PPT课件（第1.6课时）.pptx

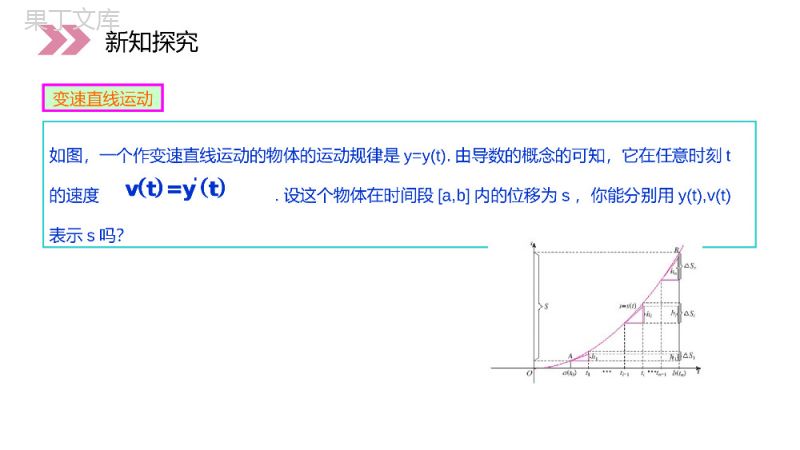
讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-21.6微积分基本定理第1章导数及其应用人教版高中数学选修2-2我们已经学习了微积分学中两个最基本和最重要的概念——导数和定积分，先回顾一下.课前导入是刻画函数变化快慢程度的一个一般概念，由于变量和函数在自然界和社会中有着几乎无处不在的实际背景，所以它是高等学校许多专业的一门重要基础课.导数的最本质思想：在每个局部小范围内“以直代曲”，“以不变代变”和逼近的思想，这也是应用定积分解决实际问题的思想方法.定积分学习微积分，数学和思维水平都将进入一个新的阶段，能切实地训练学生的辨证思维.毫不夸张地说，不学或未学懂微积分，思维难以达到较高的水平，难以适应21世纪对高中学生素质的要求.利用本节学习的微积分基本定理，我们就能轻松解决首页的问题.课前导入微积分的产生和发展被誉为“近代技术文明产生的关键事件之一，它引入了若干极其成功的、对以后许多数学的发展起决定性作用的思想.”微积分的建立，无论是对数学还是对其他科学以至于技术的发展都产生了巨大的影响，充分显示了数学对于人的认识发展、改造世界的能力的巨大促进作用.微积分是研究各种科学的工具，在中学数学中是研究初等函数最有效的工具.恩格斯称之为“17世纪自然科学的三大发明之一”.课前导入学习微积分的意义变速直线运动新知探究如图，一个作变速直线运动的物体的运动规律是y=y(t).由导数的概念的可知，它在任意时刻t的速度.设这个物体在时间段[a,b]内的位移为s，你能分别用y(t),v(t)表示s吗？'vt=yt'vt=yt函数y=y(t)在t=b处与t=a处的函数值之差.s=y(b)-y(a)物体的位移s还可利用定积分，有v(t)求位移，用分点将区间[a,b]等分成n个小区间：01i-1ia=tb时，成立.baf(x)dxF(b)F(a)新知探究baf(x)dxF(b)F(a)因为f(x)在[a,b]内连续是f(x)的一个原函数.又F(x)是f(x)的原函数，∴F(x)=+C.在上式中令x=a,则由得到C=F(a)移项得令即得xaf(t)dtxaf(t)dtaaf(t)dt=0xaf(t)dt=F(x)-Fabax=b,fxdx=Fb-Fa.证明：新知探究xaf(t)dtxaf(t)dtaaf(t)dt=0xaf(t)dt=F(x)-Fabax=b,fxdx=Fb-Fa.定积分的基本公式,又称牛顿----莱布尼兹公式.常表示为bbaaf(x)dx=F(x)=Fb-Fa.新知探究接下来让我们练一练吧bbaaf(x)dx=F(x)=Fb-Fa.例1.计算解:33-12-1dx=arctanx1+x=arctan3-arctan-1ππ7=--=π3412因为'21arctanx=1+x由微积分基本定理得：32-1dx.1+x新知探究33-12-1dx=arctanx1+x=arctan3-arctan-1ππ7=--=π3412'21arctanx=1+x32-1dx.1+x例2.计算32112x-dxx解:3332211123311112x-dx=2xdx-dxxx11=x+=9-1+-1x322=3因为''2211x=2x,=-,xx由微积分基本定理得：新知探究32112x-dxx3332211123311112x-dx=2xdx-dxxx11=x+=9-1+-1x322=3''2211x=2x,=-,xxππ00A=sinxdx=-cosx=-cosπ--cos0=2yoxxysin例3.计算正弦曲线上与x轴所围成的面积y=sinx[0,π]在解:因为'-cosx=sinx由微积分基本定理得：A新知探究ππ00A=sinxdx=-cosx=-cosπ--cos0=2yoxxysiny=sinx[0,π]在'-cosx=sinxyxo2πxysin（1）当对应的区间为时，区域A位于x轴的正上方.定积分取正值.并等于区域A的面积.0,π+Aπ0A=sinxdx新知探究yxo2πxysin0,ππ0A=sinxdx更改积分区间为，自己动手计算一下你有什么结论?π,2π,2π,0运用数形结合的思想深入探究新知探究π,2π,2π,0yox2πxysin（2）当对应的区间为时，区域A位于x轴的下方.定积分取负值.绝对值等于区域A的面积π,2-A2ππ-A=sinxdx新知探究yox2πxysinπ,22ππ-A=sinxdxyox2πxysin（3）当对应的区间为时，区域位于x轴的上方的面积等于位于x轴下方的面积.定积分值为0.且等于位于x轴上方的面积减去位于x轴下方的面积.0,2-+2π0sinxdx=0新知探究yox2πxysin0,22π0sinxdx=0ππ002π2πππ2π2π00sinxdx=-cosx=-cosπ--cos0=2sinxdx=-cosx=-cos2π--cosπ=-2sinxdx=-cosx=-cos2π--cos0=0所以得到：新知探究ππ002π2πππ2π2π00sinxdx=-cosx=-cosπ--cos0=2sinxdx=-cosx=-cos2π--cosπ=-2sinxdx=-cosx=-cos2π--cos0=01、计算.2221dxx(1+x)2、汽车以每小时36km的速度行驶,到某处需要减速停车,设汽车以等加速度刹车,问从开始刹车到停车走了多少距离?2msa=-5课堂练习22222221112211dx11=dx-dxx(1+x)x1+x11π=--arctanx=+-arctan2x241、解:因为22111-'=,arctanx'=xx1+x由微积分基本定理得：2221dxx(1+x)2msa=-522222221112211dx11=dx-dxx(1+x)x1+x11π=--arctanx=+-arctan2x2422111-'=,arctanx'=xx1+x2、解:设开始刹车时刻为则此时刻汽车速度刹车后汽车减速行驶,其速度为当汽车停住时,即得故在这段时间内汽车所走的距离为,0t361000kmmmhss03600v=36()=()=10()0v(t)=v+at=10-5t,0)(tv,0510t(s)2t22220005s=v(t)dt=(10-5t)dt=10t-t=10(m)2课堂练习,0t361000kmmmhss03600v=36()=()=10()0v(t)=v+at=10-5t,0)(tv,0510t(s)2t22220005s=v(t)dt=(10-5t)dt=10t-t=10(m)2感谢您下载68素材平台上提供的PPT作品，为了您和68素材以及原创作者的利益，请勿复制、传播、销售；素材均来源于网络用户分享，故68素材不具备充分的监控能力来审查图片是否存在侵权等情节。68素材不拥有此类图片的版权，本站所有资源仅供学习与交流，不得用于任何商业用途的范围，用户应自觉遵守著作权法及其他相关法律的规定，不得侵犯本网站及权利人的合法权利，给68素材和任何第三方造成损失的，侵权用户应负全部责任。版权声明微积分基本公式,)()(,],[)(xfxFbaCxf且设则有xxfbad)(积分中值定理))((abF)()(aFbF微分中值定理))((abf牛顿–莱布尼兹公式课堂小结,)()(,],[)(xfxFbaCxf且设xxfbad)())((abF)()(aFbF))((abf讲解人：办公资源时间：2020.6.1PEOPLE'SEDUCATIONPRESSHIGHSCHOOLMATHEMATICSELECTIVE2-2感谢你的聆听第1章导数及其应用人教版高中数学选修2-2