中考数学专题复习课件-二次函数中的面积问题

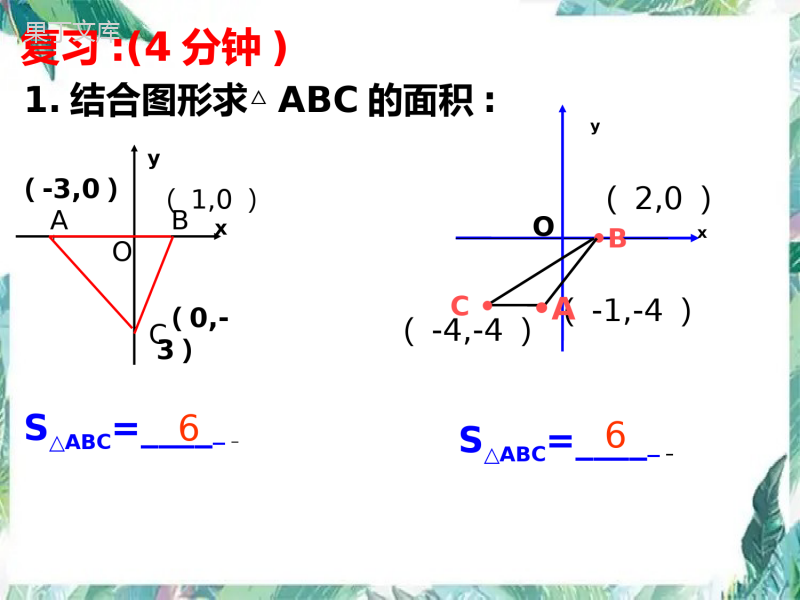
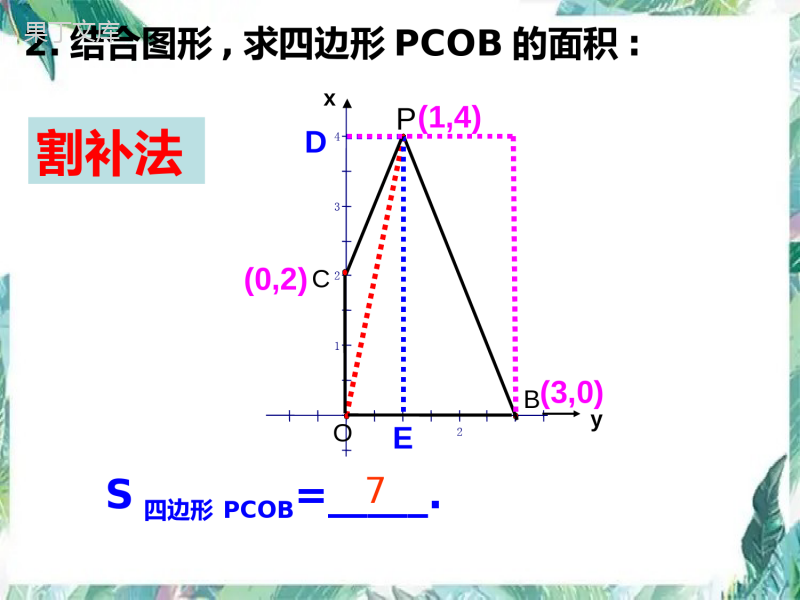
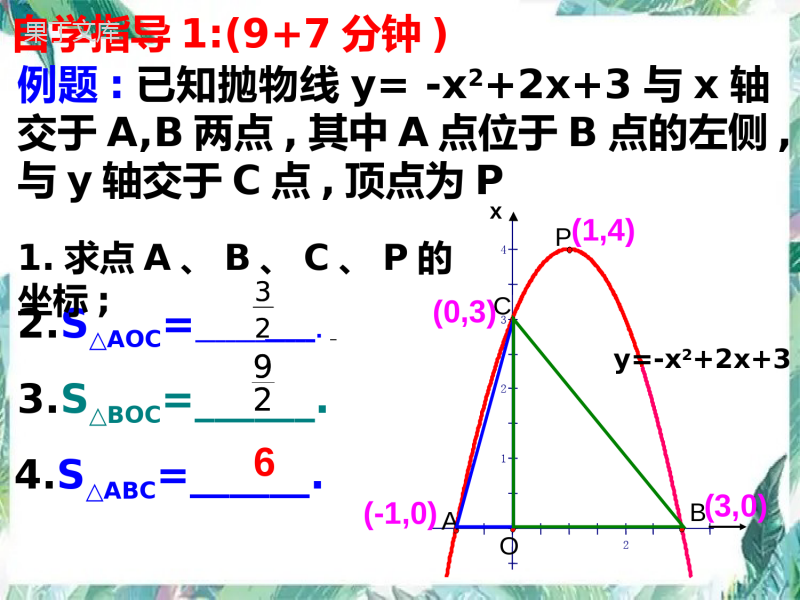
抛物线与三角(四边)形问题--------面积类中考数学专题复习O•BS△ABC=____S△ABC=____66yxCOAByx（-3,0）（1,0）（0,-3）（-1,-4）（2,0）（-4,-4）复习:(4分钟)C••A1.结合图形求△ABC的面积:43212OCPB(0,2)(3,0)(1,4)xDEy割补法S四边形PCOB=_____.72.结合图形,求四边形PCOB的面积:学习目标:(1分钟)1.能熟练的用点坐标表示线段长度;2.掌握二次函数中面积的基本求法;3.能熟练的表示面积与其它变量之间的函数关系；4.体会:特殊到一般的数学思想.例题:已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于C点,顶点为P2.S△AOC=____________.3.S△BOC=______.43212OACPB(0,3)(-1,0)(3,0)(1,4)3292x自学指导1:(9+7分钟)1.求点A、B、C、P的坐标;4.S△ABC=______.6y=-x2+2x+33292(-1,0)43212OACPB(0,3)(3,0)(1,4)x5.在抛物线上是否存在一点D,使得S△ABD=S△ABC?若存在,请求出D点坐标;若不存在,请说明理由.D1D2D3y=-x2+2x+31D(2,3)2D(1+7,-3)3D(1-7,-3)变式训练:(1)S△PAB=.(-1,0)43212OACPB(0,3)(3,0)(1,4)xy=-x2+2x+38E1E2(2)E是抛物线在x轴上方图像上的一动点,是否存在一点E使得S△EAB=S△PAB,若存在,求出E点的坐标,若不存在,请说明理由.121E(1+2,2)2E(1-2,2)自学指导2:(8+8分钟)43212OACPB(0,3)(-1,0)(3,0)(1,4)x例题:已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于C点,顶点为P,S四边形PCAB=_____.DE943212OACPB(0,3)(-1,0)(3,0)(1,4)x变式1:点E是此抛物线y=-x2+2x+3(在第一象限内)上的一个动点,设它的横坐标为m，(1)试用m的代数式表示四边形ECOB的面积S.(2)当m为多少时,S有最大值E变式2:如图,抛物线y=ax2+bx+c经过点A(-3,0),B(1,0),C(0,-3),顶点为P,(1)求抛物线的解析式；D(2)点D是此抛物线(在第三象限内)上的一个动点,设它的横坐标为m,当m为何值时,SDCOA的面积最大最大值为多少?AOPCB-3-31变式3:如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点（1）求抛物线对应的二次函数关系式;（2）在直线AC上方抛物线上有一动点D,求使△DCA面积最大的点D的坐标；（3）x轴上是否存在P点,使得以A、P、C为顶点的三角形是等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.如图,已知抛物线y=x2-x-3与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.(1)直接写出A、D、C三点的坐标;(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标.中考链接:3834(-2,0)(4,0)(0,-3)38341M(2,-3)2M(1+17,3)3M(1-17,3)变式1:如图,直线y=x-3于x轴、y轴分别交于B、C；两点,抛物线y=x2+bx+c同时经过B、C两点,点A是抛物线与x轴的另一个交点.(1)求抛物线的函数表达式；(2)若点P在线段BC上,且S△PAC=S△PAB，求点P的坐标.1212变式2:如图,抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点P、与直线BC相交于点M,连接PB．（1）求该抛物线的解析式;（2）抛物线上是否存在一点Q,使△QMB与△PMB的面积相等?若存在,求点Q的坐标;若不存在,说明理由;（3）在第一象限、对称轴右侧的抛物线上是否存在一点R,使△RPM与△RMB的面积相等?若存在,直接写出点R的坐标;若不存在,说明理由.当堂训练:1.如图,在直角坐标系中,抛物线经过点A(0，4)，B(1，0)，C(5，0)，其对称轴与x轴相交于点M．(1)求抛物线的解析式和对称轴；(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标；若不存在,请说明理由(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标；若不存在,请说明理由.2.在平面直角坐标系中,已知抛物线经过A(4﹣，0)，B(0，﹣4)，C(2，0)三点.(1)求抛物线的解析式；(2)在抛物线的对称轴上是否存在一点P,使△PBC的周长最小?若存在,请求出点P的坐标；若不存在,请说明理由；(3)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.(4)若点P是抛物线上的动点,点Q是直线y=x﹣上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.3.如图，抛物线y=-x2+x+2交x轴于A、B两点，交y轴于点C．（1）求证：△ABC为直角三角形；（2）直线x=m（0＜m＜4）在线段OB上移动，交x轴于点D，交抛物线于点E，交BC于点F．求当m为何值时，EF=DF？2123(4,0)(-1,0)(0,2)(,0)m213(,2)22mmm122yx1(,2)2mm2123(,0)m213(,2)22mmm122yx1(,2)2mm（3）连接CE和BE，若△BCE的面积存在最大值，请求出点E的坐标和△BCE的最大面积．(4,0)(-1,0)(,0)m213(,2)22mmm122yx1(,2)2mmH(,0)m213(,2)22mmm122yx1(,2)2mm4.如图，抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．（1）求此抛物线的解析式；（2）点P为抛物线上的一个动点，求使SAPC△：SACD△=5：4的点P的坐标．5.如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=1/2x﹣2+4x刻画，斜坡可以用一次函数y=x刻画．（1）请用配方法求二次函数图象的最高点P的坐标；（2）小球的落点是A，求点A的坐标；（3）连接抛物线的最高点P与点O、A得△POA求△POA的面积；（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．6.如图，在平面直角坐标系中，抛物线y=x2-2x-4与直线y=x交于点A、B，M是抛物线上一个动点，连接OM．（1）当M为抛物线的顶点时,求△OMB的面积；（2）当点M在抛物线上,OMB△的面积为10时,求点M的坐标；（3）当点M在直线AB的下方且在抛物线对称轴的右侧，M运动到何处时,OMB△的面积最大．7.如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．（1）求直线BD和抛物线的解析式．（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．（3）在抛物线上是否存在点P，使SPBD△=6？若存在，求出点P的坐标；若不存在，说明理由．谢谢指导！