常用积分公式,常用积分公式24个

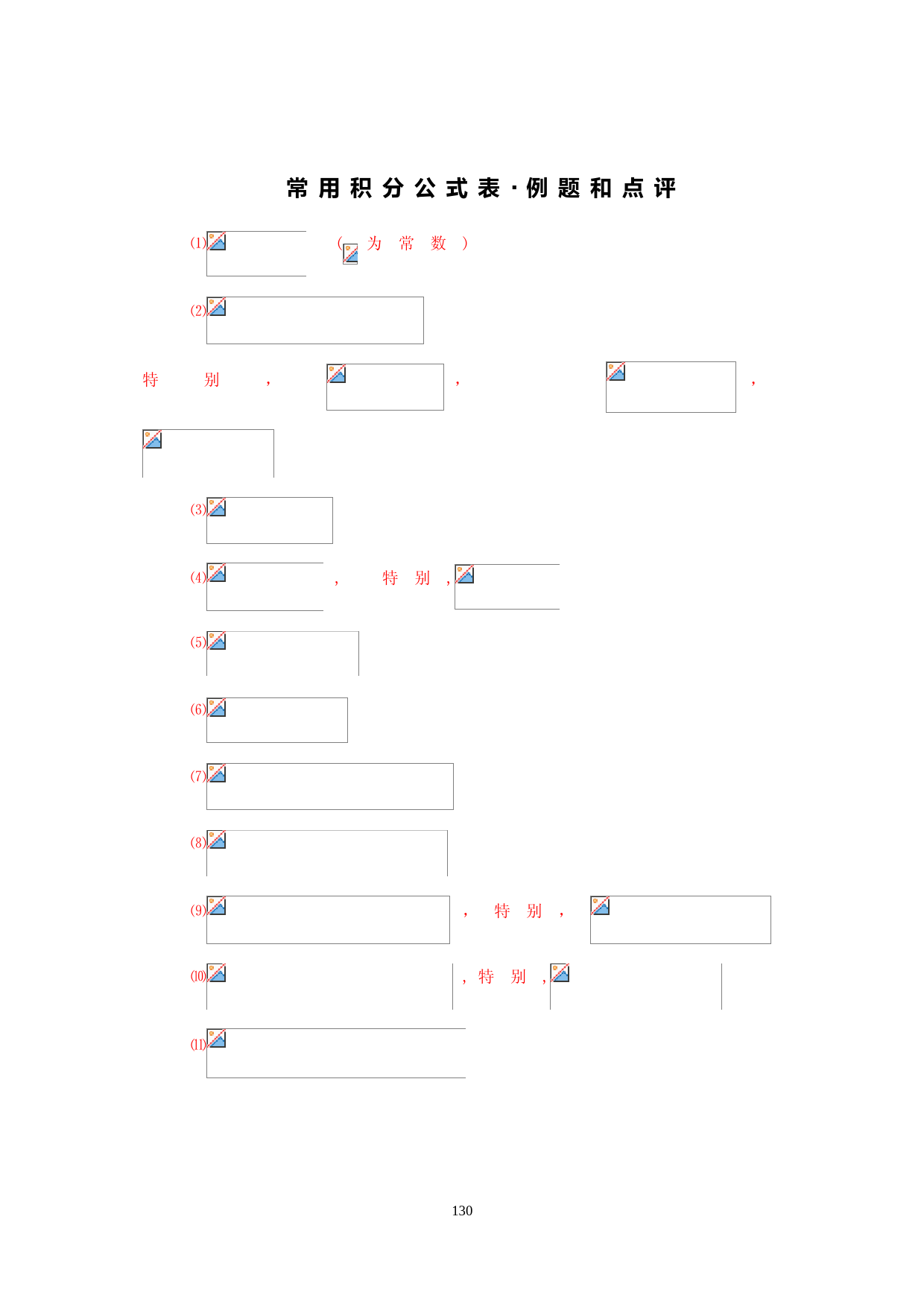
('常用积分公式表·例题和点评⑴(为常数)⑵特别，，，⑶⑷,特别,⑸⑹⑺⑻⑼，特别，⑽,特别,⑾130或⑿⒀⒁⒂⒃⒄⒅⒆⒇（递推公式)跟我做练习(一般情形下，都是先做恒等变换或用某一个积分法，最后套用某一个积分公式)例24含根式的积分131⑴[套用公式⒅］⑵（请你写出答案)⑶［套用公式⒃］⑷(请你写出答案）⑸［套用公式⒄］⑹(请你写出答案)⑺[套用公式⑼]⑻132（请你写出答案)例25求原函数.解因为所以令从恒等式（两端分子相等)，可得方程组解这个方程组（在草纸上做)，得。因此,右端的第一个积分为(套用积分公式）133类似地，右端的第二个积分为所以（见下注）【注】根据，则因此，例26求.【关于，见例17】解令(半角替换），则于是，134【点评】求初等函数的原函数的方法虽然也有一定的规律，但不像求它们的微分或导数那样规范化.这是因为从根本上说，函数的导数或微分可以用一个“构造性"的公式或确定下来，可是在原函数的定义中并没有给出求原函数的方法。积分法作为微分法的逆运算其运算结果有可能越出被积函数所属的函数类譬如，有理函数的原函数可能不再是有理函数初等函数的原函数可能是非初等函数(这就像正数的差有可能是负数、整数的商有可能是分数一样）。有的初等函数尽管很简单,可是它的原函数不能表示成初等函数，譬如等都不能表示成初等函数.因此，一般说来求初等函数的原函数要比求它们的微分或导数困难得多.我们用上面那些方法能够求出原函数的函数，只是初等函数中的很小一部分.尽管如此,我们毕竟可以求出足够多函数的原函数，而这些正好是应用中经常遇到的函数.因此，读者能够看懂前面那些例题并能够基本完成各节后的练习就足够了。135',)