九上人教版数学22.1.2y=ax2的图像和性质

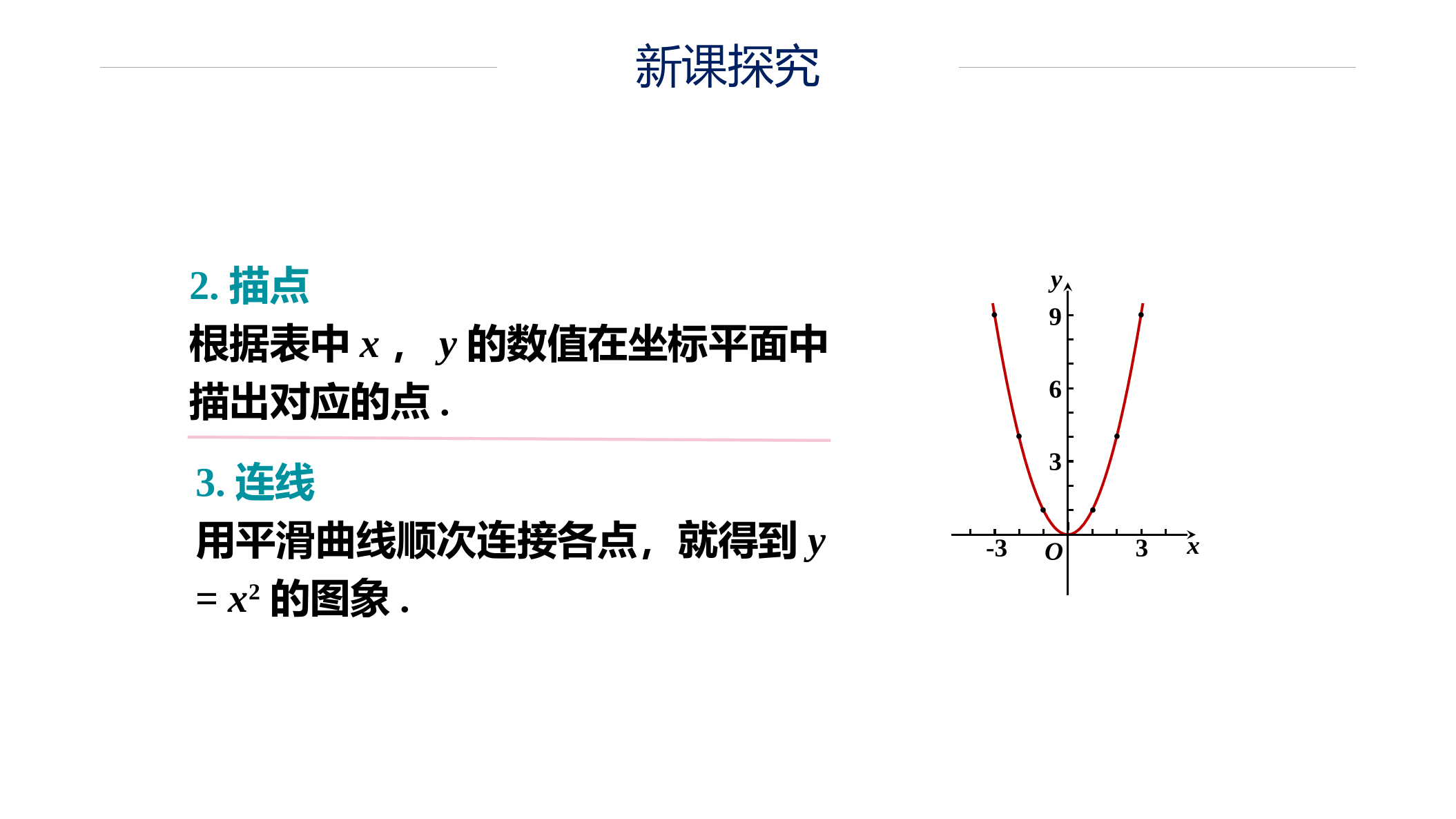
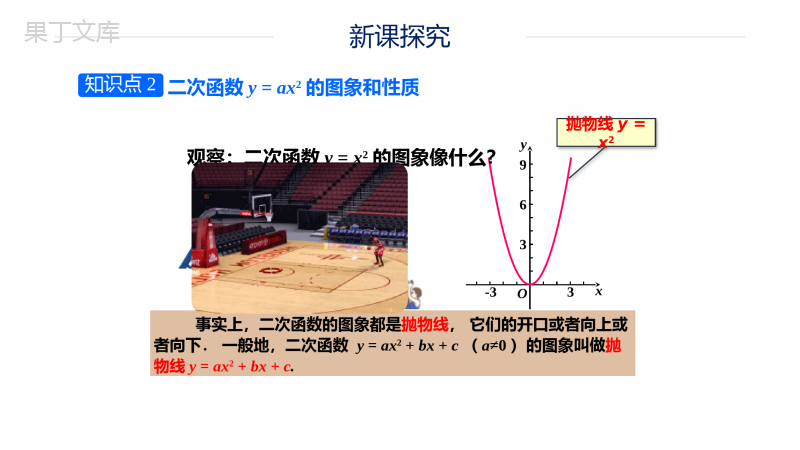
九上人教版数学二次函数y=ax2的图像与性质回忆说出思考方法我们学过的函数图像一次函数与反比例函数的形状如何画函数图像呢？1列表、2描点、3连线新课导入新课探究先画二次函数y=x2的图象x···-3-2-10123···y=x2···9410149···1.列表在y=x2中，自变量x可以是任意实数，列表表示出几组对应值：知识点1二次函数y=ax2的图象的画法新课探究2.描点根据表中x，y的数值在坐标平面中描出对应的点.3.连线用平滑曲线顺次连接各点，就得到y=x2的图象.369yO-33x新课探究369yO-33x观察：二次函数y=x2的图象像什么？事实上，二次函数的图象都是抛物线，它们的开口或者向上或者向下．一般地，二次函数y=ax2+bx+c（a≠0）的图象叫做抛物线y=ax2+bx+c.抛物线y=x2知识点2二次函数y=ax2的图象和性质新课探究369yO-33x函数y=x2的图象开口______.向上抛物线与对称轴的交点叫做抛物线的顶点。这条抛物线关于y轴对称，y轴就是它的对称轴.顶点坐标是________.顶点是图象的最____点.（0，0）低在抛物线y=x2上任取一点（m，m2），因为它关于y轴的对称点（-m，m2）也在抛物线y=x2上，所以抛物线y=x2关于y轴对称。特征实际上，每条抛物线都有对称轴，抛物线与对称轴的交点叫做抛物线的顶点.顶点是抛物线的最低点或最高点．新课探究369yO-33x当x<0(在对称轴的左侧)时，y随着x的增大而减小.当x>0(在对称轴的右侧)时，y随着x的增大而增大.单调性新课探究268y4O-22x4-4解：分别列表，再画出它们的图象，如图.x···-4-3-2-101234······84.520.500.524.58···x···-2-1.5-1-0.500.511.52···y=2x2···84.520.500.524.58···212yxy=2x2221xy例1在同一直角坐标系中，画出函数，y=2x2的图象.221xy新课探究a值越大，抛物线的开口越小．增减性相同：当x<0时，y随x增大而减小；当x>0时，y随x增大而增大.268y4O-22x4-4212yxy=2x2顶点都是原点(0，0)，顶点是抛物线的最低点；开口都向上；对称轴都是y轴；函数的图象与函数y=x2的图象相比，有什么共同点和不同点？yxyx221==22，笔记总结一般地，当a>0时，抛物线y=ax2的开口向上，对称轴是y轴，顶点是原点，顶点是抛物线的最低点，a越大，抛物线的开口越小.268y4O-22x4-4212yxy=2x2笔记总结画出函数y=-x2,,y=-2x2的图象，并思考这些抛物线有什么共同点和不同点．212yxx···-3-2-10123···y=-x2···-9-4-10-1-4-9······-20-2···y=-2x2···-18-8-20-2-8-18···212yxy=-2x2y=-x22129221xy2129-3-6-9yO-33x笔记总结212yxy=-2x2y=-x2-3-6-9yO-33x开口都向下；对称轴都是y轴；a值越小，抛物线的开口越小．顶点都是原点(0，0)，顶点是抛物线的最高点；增减性相同：当x<0时，y随x增大而增大；当x>0时，y随x增大而减小.共同点和不同点一般地，当a<0时，抛物线y=ax2的开口向下，对称轴是y轴，顶点是原点，顶点是抛物线的最高点，a越小，抛物线的开口越小.笔记总结1.二次函数的图象都是抛物线.2.抛物线y=ax2的图象性质:（2）当a>0时，抛物线的开口向上，顶点是抛物线的最低点;当a<0时，抛物线的开口向下，顶点是抛物线的最高点;a越大，抛物线的开口越小.（1）抛物线y=ax2的对称轴是y轴，顶点是原点.212yxy=-2x2y=-x2268y4212yxy=2x2-8-4-2-6O-22x4-41.抛物线y＝x2不具有的性质是（）.A.开口向上B.与x轴不相交C.对称轴是y轴D.最低点是坐标原点2、己知二次函数y=ax2(a≠0)图象经过点A(-1,)和B(3,m),(1)求a与m的值：(2)写出二次函数图象的顶点坐标及对称轴：(3)当-3≤x≤1时，求函数y的最大值和最小值。解：(1)将A(-1,)代入y=ax2(a≠0)，得a=将B(3,m)代入y=，得m=3(2)二次函数图象的顶点坐标为(0,0)，对称轴是y轴。(3)最大值是y=3,最小值是y=0.B练习3.抛物线y＝最小值，则k=4.当-时，求二次函数的最大值和最小值最大值y=0，最小值y=-8练习1THANKYOU