反比例函数的图象和性质(第2课时)(课件)-九年级数学上册同步精品课堂(北师大版)

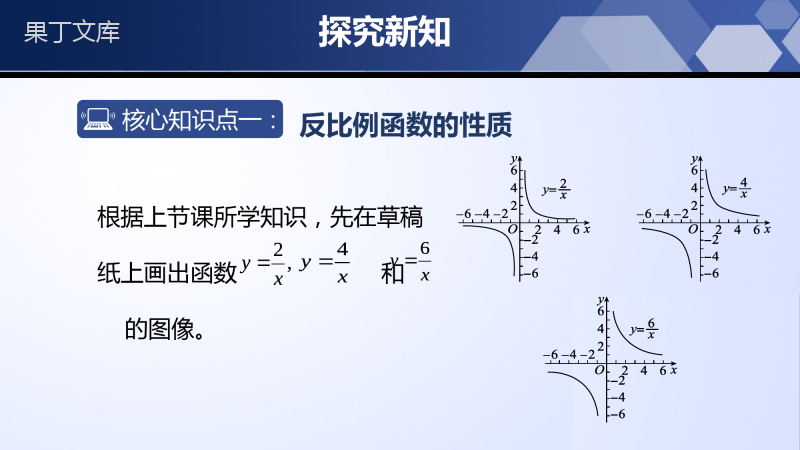
新课标北师大版九年级上册6.2.2反比例函数的图象和性质（第2课时）第六章反比例函数学习目标1.熟悉作函数图象的主要步骤，能熟练地作出反比例函数的图象。2.能从函数图象中获取信息，掌握反比例函数的主要性质。3.能运用反比例函数的性质，解决问题。情境导入1.反比例函数的图象是什么？双曲线2.反比例函数的对称性是什么？既是中心对称图形（原点为对称中心）又是轴对称图形（y=x和y=-x为对称轴）情境导入同学们还记得反比例函数图象的特点吗?反比例函数图象性质当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.由两支曲线组成0kykx0kykx探究新知核心知识点一：反比例函数的性质根据上节课所学知识，先在草稿纸上画出函数和的图像。xy42,yxxy6xy42,yxxy6探究新知思考：(1)函数图象分别位于哪几个象限?函数的图像都位于一、三象限(2)在每一个象限内，随着x值的增大y的值是怎样变化的?能说明这是为什么吗？在每一个象限内，随着x值的增大，y越来越小。(3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗？为什么？与x轴、y轴不相交，因为对于反比例函数x≠0，所以y≠0探究新知归纳总结①由两条曲线组成②分别位于第一、三象限③它们与x轴、y轴都不相交④在每个象限内，y随x的增大而减小反比例函数(k＞0)的图象和性质：kyxkyx探究新知yxO2yxyxO4yxyxO6yx思考：在函数y＝中，当k<0时，结果又如何呢？画出y＝-，y＝-,y=-的图象,观察图像的特点.x2x4x6kx2yx4yx6yxx2x4x6kx探究新知归纳总结（1）函数的图像都位于第二、四象限（2）在每一个象限内，随着x值的增大而增大（3）反比例函数的图像与x轴、y轴不相交k的正负决定反比例函数所在的象限和增减性反比例函数(k<0)的图象和性质：kyxkyx探究新知反比例函数k的符号k＞0k＜0图像性质1.x的取值范围是x≠0，y的取值范围是y≠0;2.函数图像的两个分支分别在第一、三象限。在每个象限内，y随x的增大而减小1.x的取值范围是x≠0，y的取值范围是y≠0;2.函数图像的两个分支分别在第二、四象限；在每个象限内，y随x的增大而增大)0(kxky)0(kxky探究新知函数正比例函数反比例函数表达式图象及象限性质在每一个象限内:当k>0时，y随x的增大而减小;当k<0时，y随x的增大而增大.y=kx(k≠0)(特殊的一次函数)当k>0时，y随x的增大而增大;当k<0时，y随x的增大而减小.k<0xyoxyok>0k<0yx0y0k>0x0)k(kxy或kxy或xky10)k(kxy或kxy或xky1探究新知核心知识点二：反比例函数解析式中k的几何意义在一个反比例函数图象任取两点A、B，过点A分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为；过点B分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为，与有什么关系？为什么？1S2S1S2S1S2S1S2S探究新知xy2因为A,B为图象上的点，所以满足，.过A作AA1x⊥轴于A1，AA2x⊥轴于A2，于是有A1（a，0），A2(0，)，所以矩形AA1OA2的面积为＝；同理矩形BB1OB2的面积为＝.22aa22bb2a1S2S22aa22bb1S2S（1）对于具体的反比例函数，此时与有什么关系？为什么？1S2Sxy2xy222aa22bb2a1S2S22aa22bb1S2S1S2Sxy2探究新知两个矩形面积相等，都等于横坐标与纵坐标绝对值的乘积.思考：对于反比例函数，有怎样的结论？2yx过反比例函数图象上任一点分别作x轴、y轴的平行线，与坐标轴围成的矩形面积为：S矩＝k.（2）对于一般反比例函数，此时与有什么关系？为什么？0kykx1S2S2yx0kykx1S2S探究新知在一个反比例函数图象任取点A，过点A作y轴的平行线（或作x轴的平行线），连接OA，与坐标轴围成的三角形面积为S，S有什么特点？为什么？xyOA过反比例函数图象上任一点，作x轴或y轴的平行线，并连接该点与坐标原点，与坐标轴所围成的三角形面积为：，即.2△kS12△SS矩2△kS12△SS矩探究新知归纳总结对于反比例函数点Q是其图象上的任意一点作QA垂直于y轴，作QB垂直于x轴矩形AOBQ的面积与k的关系是S矩形AOBQ=xkyAByxO因为k有正负，多以表达面积的时，要加上绝对值符号Qk2k推理：△QAO与△QBO的面积和k的关系是S△QAO=S△QBO=xkyk2k随堂练习1.如图，点P在反比例函数y=（k≠0）的图象上，PAx⊥轴于点A，△PAO的面积为2，则k的值为（）A.1B.2C.4D.6C随堂练习2.如图，A，B两点在双曲线y=上，分别经过A，B两点向坐标轴作垂线段，已知S阴影=1.7，则S1+S2=（）A.4B.4.2C.4.6D.5C随堂练习3.若函数y=的图象与直线y=-x没有交点，则k的取值范围是（）A.k>1B.k<1C.k>-1D.k<-1B随堂练习4.已知函数y1=x（x≥0），y2=（x>0）的图象如图所示，给出下列结论：①两函数图象的交点坐标为（2，2）；②当x>2时，y2>y1；③直线x=1分别与两函数图象交于B，C两点，则线段BC的长为3；④当x逐渐增大时，y1的值随着x的增大而增大，y2的值随着x的增大而减小.其中正确的是（）A.①②B.①③C.D.②④①③④D随堂练习5.如图，直线与双曲线交于A，B两点，P是AB上的点，△AOC的面积S1、△BOD的面积S2、△POE的面积S3的大小关系为.S1=S2y2时，x的取值范围为.-23随堂练习7.如图，一次函数y1=k1x+b（k1≠0）的图象与反比例函数y2=的图象交于A，B两点，观察图象，当y1