角平分线的作法和性质-2022-2023学年八年级数学上册同步精品课件(沪科版)

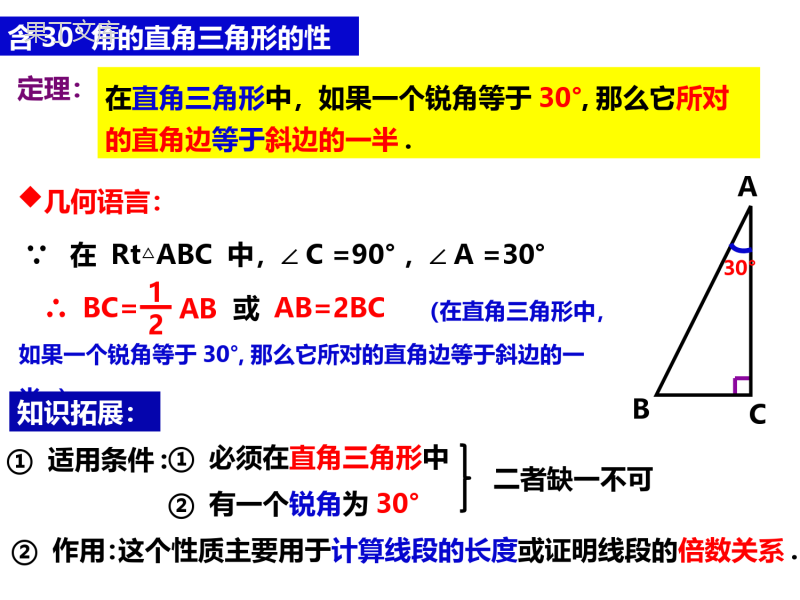
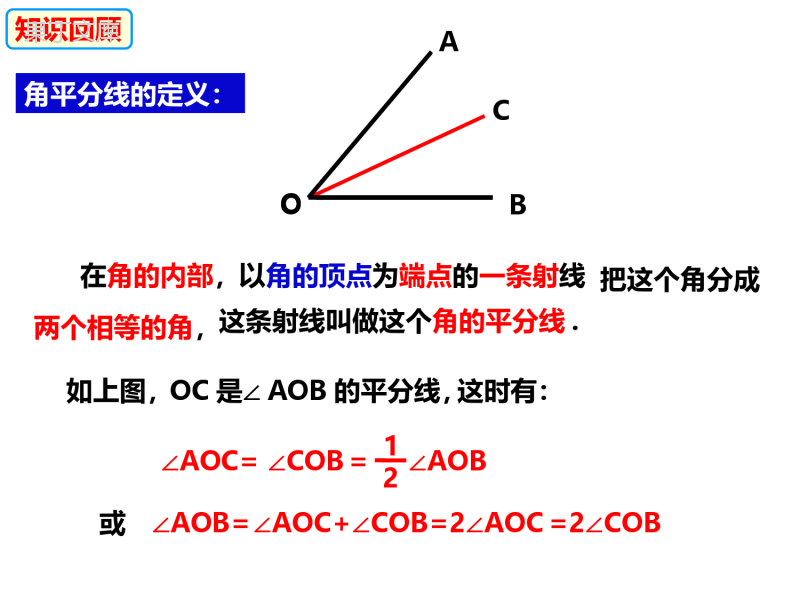
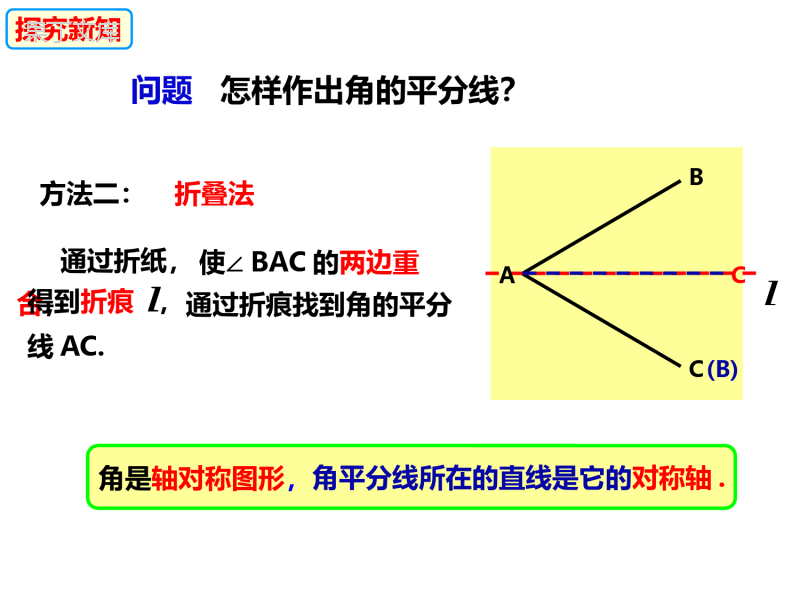
（在直角三角形中，如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.）在直角三角形中，如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.含30°角的直角三角形的性质定理：∵在Rt△ABC中，∠C=90°，∠A=30°ABC几何语言：∴BC=12AB30°或AB=2BC知识拓展：①适用条件:①必须在直角三角形中②有一个锐角为30°二者缺一不可②作用：这个性质主要用于计算线段的长度或证明线段的倍数关系.15.4角平分线的作法和性质知识回顾角平分线的定义：把这个角分成两个相等的角，这条射线叫做这个角的平分线.在角的内部，如上图，∠AOC==∠AOB或=2∠AOC12以角的顶点为端点的一条射线OC是∠AOB的平分线，这时有：BAOOC∠COB∠AOB==2∠COB∠AOC+∠COB探究新知问题怎样作出角的平分线？再用量角器画出这个角的平分线.度量法方法一：先用量角器量出已知角的度数，并除以2，通过折痕找到角的平分线AC.探究新知问题怎样作出角的平分线？BC使∠BAC的两边重合，折叠法方法二：通过折纸，得到折痕，A(B)llC角是轴对称图形，角平分线所在的直线是它的对称轴.ll问题怎样作出角的平分线？探究新知BAMNPＯ用尺规作图法，方法三：作出∠AOB的平分线.作法：任意长为半径画弧1、以点O为圆心，12以大于MN长为半径分别交OA，OB于点M，N.2、分别以点M，N为圆心，(为什么?)在角的内部画弧交于点P.3、做射线OP，则OP为所作的∠AOB的平分线.思考1根据作图，你能证明所作射线OP，就是∠AOB的平分线吗？BAMNPＯ已知：OM=ON，PM=PN.求证：OP平分∠AOB.证明：在△OMP和ONP中∵OM=ONPM=PNOP=OP(已知)(已知)(公共边)∴△OMP≌△ONP(SSS)∴∠MOP=∠NOP∴OP平分∠AOB(全等三角形的对应角相等)(角平分线的定义)探究新知探究新知两弧相交于点P.思考2当∠AOB的两边成一直线时(即∠AOB=180°)，你会作这个角的平分线吗？这时的角平分线OP与直线AB是什关系？作法：任意长为半径画弧1、以点O为圆心，分别交OA，OB于点M，N12以大于MN长为半径画弧，2、分别以点M，N为圆心，3、作射线OP，则OP为所作的∠AOB的平分线.ABONMPOP⊥AB探究新知通过上面作图，你能用尺规完成“经过一点作已知直线的垂线”吗？由于这一点可能在直线上或直线外，这个作图要分为两种情况：①经过已知直线上的一点作这条折线的垂线.②经过已知直线外一点作这条直线的垂线.①经过已知直线上的一点作这条直线的垂线.操作已知：直线AB和AB上的一点C.求作：AB的垂线，使它经过点C.两弧相交于点F.作法：任意长为半径画弧1、以点C为圆心，分别交CA，CB于点D，E.12以大于DE长为半径画弧，2、分别以点M，N为圆心，3、作直线CF，则直线CF为所求作的直线.ABCEDF思考：为什么这样作出的直线CF就是所求作的垂线，你能说说道理吗？②经过已知直线外一点作这条直线的垂线.已知：直线AB和AB外上的一点C.求作：AB的垂线，使它经过点C.两弧相交于点F.作法：1、以点C为圆心，以大于点C到直线AB的距离的线段长为半径画弧，12以大于DE长为半径画弧，2、分别以点D和点E为圆心，3、作直线CF，则直线CF为所求作的直线.ABCDEF交AB于点D和E；思考：为什么这样作出的直线CF就是所求作的垂线，你能说说道理吗？操作1、如图，在△ABC中，作∠ABC的平分线BD，交AC于D，作线段BD的垂直平分线EF，分别交AB于E，BC于F，垂足为O，连接DF．在所作图中，寻找一对全等三角形，并加以证明.(不写作法，保留作图痕迹)对应练习2、尺规作图：请在下图作出一个∠AOC，使其是已知∠AOB的倍.32(要求保留作图痕迹，在所作图中标上必要的字母，不写作法和结论.)ABMNPＯC对应练习P思考：如图，OP是∠AOB的平分线，P是OP上的任意一点，过点P分别作PC⊥OA，PD⊥OB，点C，D是垂足.量一量PC和PD的长度，你能发现什么？你能证明你的猜想吗？PBAＯCDPC=PDCDPCD猜想：角平分线上的点到角两边的距离相等.由此你能得到什么猜想？探究新知验证猜想猜想：角平分线上的点到角两边的距离相等.证明：∵PC⊥OA，PD⊥OB∴∠PCO=∠PDO=90°在△PCO和△PDO中，∠AOP=∠BOP∠PCO=∠PDOOP=OP∴△PDO≌△PEO∴PC=PDPBAＯCD已知：如图，OP平分∠AOB，点P是OP上的任意一点，PC⊥OA，PD⊥OB，垂足分别为C，D.求证：PC=PD.∵OP平分∠AOB∴∠AOP=∠BOP(角平分线的定义)(垂直的定义)∵(公共边)(AAS)(全等三角形的对应边相等)角平分线上的点到角两边的距离相等.归纳总结角平分线的性质：定理：PBAＯCD点到角两边垂线段的长度使用条件：①点一定要在角平分线上②点到角两边的距离性质定理的作用：可用来证明两条线段相等.是指几何语言：∵OP是∠AOB的平分线，∴PC=PD(角平分线上的点到角两边的距离相等)且PC⊥OA，PD⊥OB推理的理由有三个，必须写完整，不能少了任何一个.(角平分线上的点到角两边的距离相等)(角平分线上的点到角两边的距离相等)(角平分线上的点到角两边的距离相等)CABD图①图②CBAD巩固练习1、判断下列各题是否正确地使用了角的平分线的性质?(1)如图①∵AC平分∠BAD∴DC=BC(2)如图②∵BC⊥AB，DC⊥AD∴DB=DC(3)如图②∵AD平分∠BAC，DC⊥AC且DB⊥AB，∴BD=CD××√2、如图，OP为∠AOB的角平分线，PC⊥OA，PD⊥OB，垂足分别是C、D，则下列结论错误的是（）A.PC=PDB.OC=ODC.∠CPO=∠DPOD.∠CPD=∠DOCD巩固练习巩固练习3、如图，已知OC是∠AOB的角平分线，点D、F分别是射线OC、OA的动点，DE⊥OB于E且DE=3cm，则线段DF的最小值是cm.3F4、如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC＝5，DE＝2，则△BCE的面积等于()A．10B．7C．5D．4CF巩固练习5、如图，PA、PC分别是△ABC外角∠MAC与∠NCA的平分线，并交于点P，PD⊥BM于点D，PF⊥BN于点F.求证：BP是∠MBN的平分线．巩固练习E知识拓展：过角平分线上的一点向角两边作垂线段，再利用角平分线的性质定理解决问题.解决有关角平分线问题最常用的作辅助线的方法：6、已知：如图，在△ABC中，AD是它的角平分线，且BD=CD，DE⊥AB，DF⊥AC，垂足分别为E，F.求证：EB=FC.ABCDEFDF⊥AC∠DEB=∠DFC=90°在Rt△BDE和Rt△CDF中DE=DFBD=CD∴Rt△BDE≌Rt△CDF∴EB=FC证明：∵AD是∠BAC的角平分线，且DE⊥AB，∴DE=DF(角平分线上的点到角两边的距离相等)(垂直的定义)∵(HL)(全等三角形的对应边相等)(已知)(已证)7、如图，CD是∠AOB平分线上的点，CE⊥OA于点E，CF⊥OB于点F，求证：∠CDE=∠CDF.8、如图，在△ABC中，∠C＝90°，BC＝AC，AD是∠BAC的平分线，DE⊥AB于点E.若AB＝10cm，求△DBE的周长．解:∵AD平分∠CAB，DE⊥AB∴DC＝DE(角平分线上的点到角两边的距离相等)在Rt△ACD和Rt△AED中DC=DEAD=AD∴Rt△ACD≌Rt△AED∴AC=AE∵(HL)(全等三角形的对应边相等)(公共边)(已证)∵AC=BC∴AE=BC∴△DBE的周长=DE+DB+EB且∠C＝90°，=CD+DB+EB=BC+EB=AE+EB=AB又∵AB＝10cm∴△DBE的周长为10cm9、如图所示，BD是∠ABC的角平分线，DE⊥AB，垂足分别为E，S△ABC=60cm2，AB=18cm，BC=12cm，求DE的长．巩固练习F10、如图，AE∥CF，AG、CG分别平分∠EAC和∠FCA，过点G的直线BD⊥AE，交AE于B，交CF于D.求证：AB+CD=AC.H巩固练习11、如图，D是∠EAF的平分线上的一点，点B，C分别在AF，AE上，若∠ACD+∠ABD=180°.求证：CD=BD.巩固练习NM角平分线上的点到角两边的距离相等.归纳总结角平分线的性质：定理：PBAＯCD点到角两边垂线段的长度使用条件：①点一定要在角平分线上②点到角两边的距离性质定理的作用：可用来证明两条线段相等.是指几何语言：∵OP是∠AOB的平分线，∴PC=PD(角平分线上的点到角两边的距离相等)且PC⊥OA，PD⊥OB推理的理由有三个，必须写完整，不能少了任何一个.