中考专题-十字模型,中考对角互补模型专题

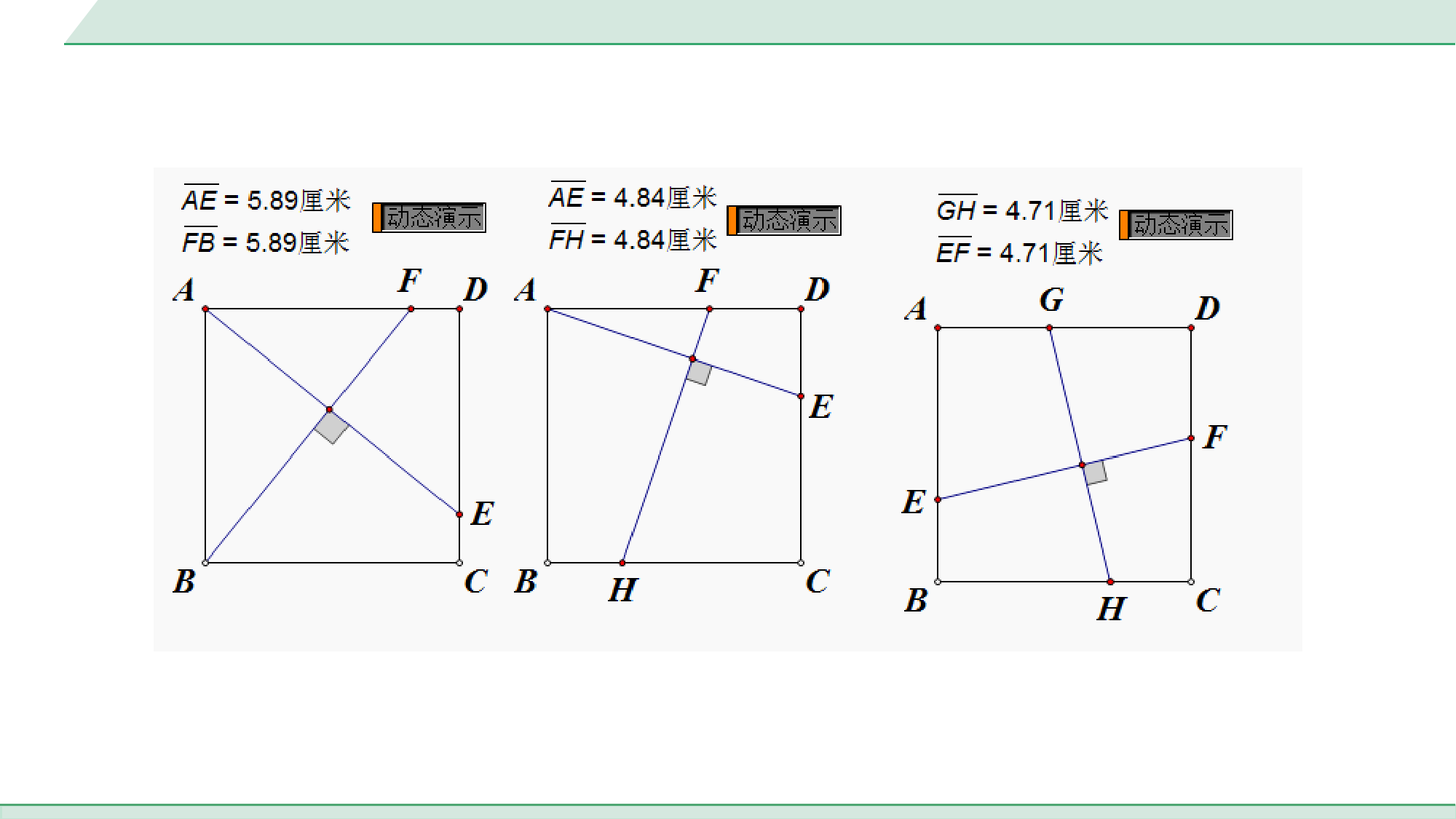
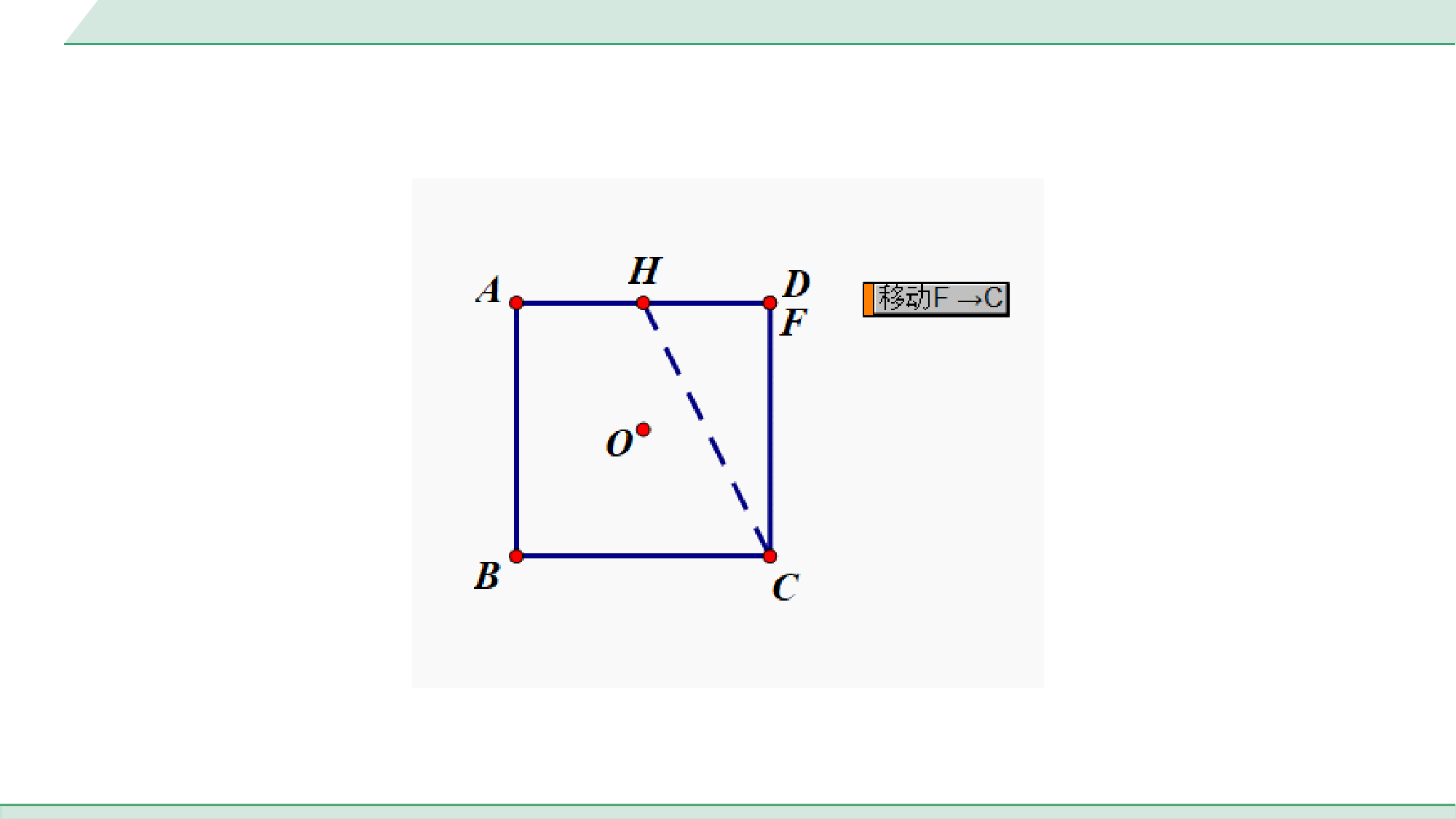
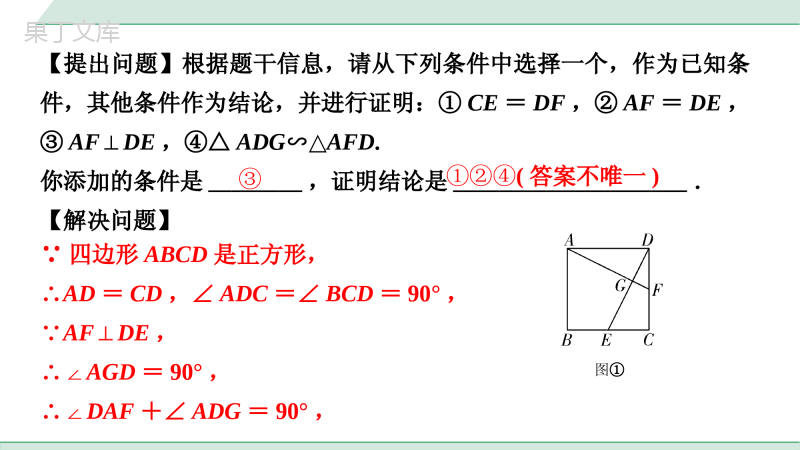
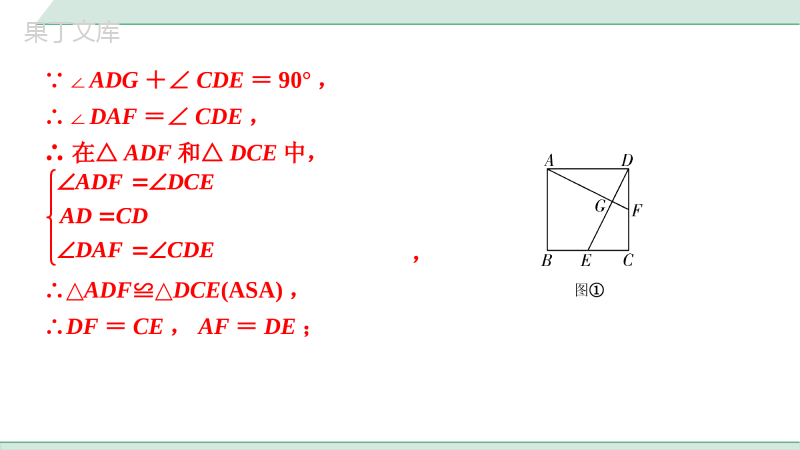
中考专题十字模型【活动目的】运用所学的知识探究正方形中十字图形的特点及相关结论.活动1:【分析图形】如图①,在正方形ABCD中,点E、F分别是BC、CD上的点,AF、DE相交于点G.图①【提出问题】根据题干信息,请从下列条件中选择一个,作为已知条件,其他条件作为结论,并进行证明:①CE=DF,②AF=DE,③AF⊥DE,④△ADG∽△AFD.你添加的条件是________,证明结论是____________________.【解决问题】③①②④(答案不唯一)∵四边形ABCD是正方形,∴AD=CD,∠ADC=∠BCD=90°,∵AF⊥DE,∴∠AGD=90°,∴∠DAF+∠ADG=90°,图①∵∠ADG+∠CDE=90°,∴∠DAF=∠CDE,∴在△ADF和△DCE中,,∴△ADF≌△DCE(ASA),∴DF=CE,AF=DE;ADFDCEADCDDAFCDE图①ADFDCEADCDDAFCDE在△ADG和△AFD中,,∴△ADG∽△AFD.AGDADFDAGFAD【总结结论】______________________________________________________________________________________________________________________________________________________;如题图,在正方形ABCD中,点E、F分别是BC、CD上的点,AF、DE相交于点G.若AF⊥DE,则有CE=DF,AF=DE,△ADG∽△AFD.图①AGDADFDAGFAD活动2:【类比探究】如图②当点E、F分别在正方形ABCD的边CB、DC的延长线上时,活动1中添加条件是否仍然可以证明相应的结论?说明理由.图②仍然可以.理由:∵四边形ABCD是正方形,∴AD=CD,∠ADC=∠BCD=90°,∵AF⊥DE,∴∠AGD=90°,∴∠DAF+∠ADG=90°,∵∠ADG+∠CDE=90°,∴∠DAF=∠CDE,∴在△ADF和△DCE中,,∴△ADF≌△DCE(ASA),∴DF=CE,AF=DE;ADFDCEADCDDAFCDE图②ADFDCEADCDDAFCDE在△ADG和△AFD中,,∴△ADG∽△AFD.AGDADFDAGFAD图②AGDADFDAGFAD活动3:【挖掘本质】问题1:如图③,当点E、F分别在BC、CD上运动,且CE=DF,点G到哪条边中点的距离始终不变?为什么?图③AD理由:∵AF⊥DE,∴∠AGD=90°,∴点G的运动轨迹是以AD中点为圆心,以AD为直径的一条圆弧,∴点G到AD的中点的距离始终不变.1414问题2:根据点G的运动轨迹你能发现什么结论?图③点G的运动轨迹是以AD中点为圆心,以AD为直径的一条圆弧.1414活动4:【知识迁移】运用所学的知识探究矩形中十字图形的特点.问题:如图④,在矩形ABCD中,AB=m,AD=n,点E是AD上一点,且CE⊥BD,则CE与BD之间有什么数量关系?然后给予证明.图④CE与BD之间的数量关系为.CEmBDn证明:∵四边形ABCD是矩形,∴∠BCD=∠CDE=90°,∴∠BDE+∠BDC=90°,CEmBDn∵CE⊥BD,∴∠BDE+∠DEC=90°,∴∠BDC=∠DEC,∴△CDE∽△BCD,∴.CECDABmBDBCADn图④CECDABmBDBCADn【真题再现】1.在正方形ABCD中,如图①,点E是AB边上的一个动点(点E与点A、B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:△ABF≌△BCE;图①第1题图(1)证明:∵BF⊥CE,∴∠CGB=90°,∴∠GCB+∠GBC=90°,又∵四边形ABCD为正方形,∴BC=AB,∠FAB=∠EBC=90°,∠GBA+∠GBC=90°,∴∠GCB=∠FBA,在△ABF与△BCE中,,∴△ABF≌△BCE(ASA);FBAECBABBCFABEBC图①第1题图FBAECBABBCFABEBC(2)当点E运动到AB中点时,连接DG.①如图②,若AB=2,求DG的长;图②第1题图∵E为AB中点,AB=2,∴EB=1,BC=AB=2,∴CE=,在Rt△CEB中,由CE·BG=EB·BC得BG=,∴CG=,222215BCEB122555EBBCCE22455BCBG∟H(2)解:①如解图①,过点D作DH⊥CE于点H,222215BCEB122555EBBCCE22455BCBG∵∠DCE+∠BCE=∠BCE+∠CBF=90°,∴∠DCE=∠CBF,在△CHD与△BGC中,∴△CHD≌△BGC(AAS),∴CH=BG=,∴GH=CG-CH==CH,,CHDBGCDCHCBGDCCB255255图②第1题图∟H,CHDBGCDCHCBGDCCB255255在△DGH与△DCH中,∴△DGH≌△DCH(SAS),∴DG=DC=2;,GHCHGHDCHDDHDH图②第1题图∟H,GHCHGHDCHDDHDH②如图③,过点C作CM⊥DG于点H,分别交AD、BF于点M、N,求的值.图③第1题图②设正方形ABCD的边长是m,则BE=,∴CE=m.易得△BCG∽△ECB,∴,∴CG=m.2mCGBCCEEC2255BCCE22522mm2mCGBCCEEC2255BCCE22522mm∴CP=CG=m,∴DP=.∴S△DCG=CG·DP=.又∵S△DCG=DG·CH,由(2)得DG=DC=m,∴CH=.易得△CGN∽△CHG,△CDM∽△CHD,55122252555mmm1221252522555mmm1245m图③第1题图如解图②,作DP⊥CG于点P,由(2)可知点P是CG的中点,∟P55122252555mmm1221252522555mmm1245m∴,∴CN=,CM=,∴MN=CM-CN=,NH=CN-CH=m-=,∴.,CNCGCMCDCGCHCHCH254CDmCH2CGmCH4m45m5m54MNNH图③第1题图∟P,CNCGCMCDCGCHCHCH254CDmCH2CGmCH4m45m5m54MNNH
提供中考专题-十字模型,中考对角互补模型专题会员下载,编号:1701028376,格式为 xlsx,文件大小为21页,请使用软件:wps,office Excel 进行编辑,PPT模板中文字,图片,动画效果均可修改,PPT模板下载后图片无水印,更多精品PPT素材下载尽在某某PPT网。所有作品均是用户自行上传分享并拥有版权或使用权,仅供网友学习交流,未经上传用户书面授权,请勿作他用。若您的权利被侵害,请联系963098962@qq.com进行删除处理。

 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载 下载
下载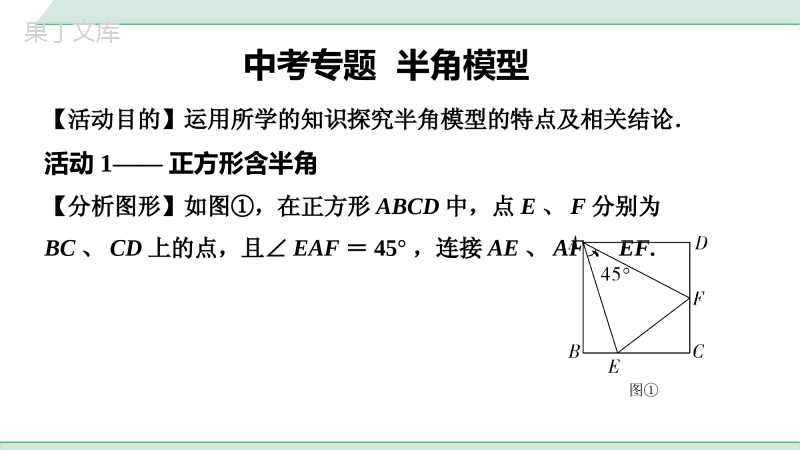 下载
下载 下载
下载 下载
下载 下载
下载