隐圆-模型(1) (1),隐圆模型最全汇总

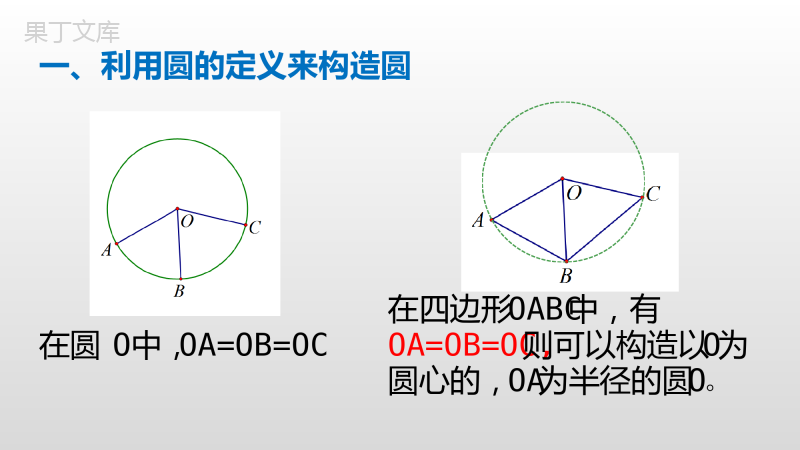
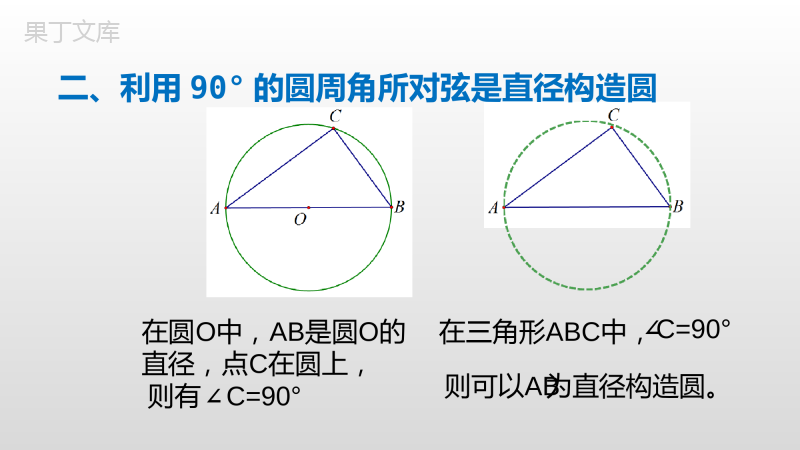
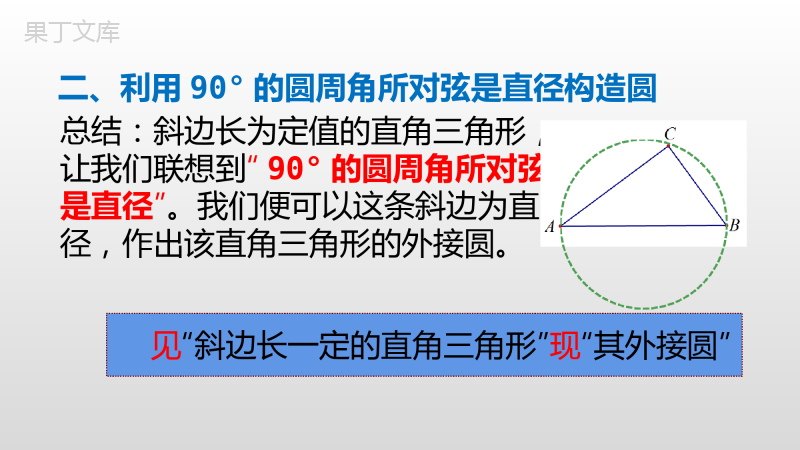
隐圆中考专题一、利用圆的定义来构造圆在圆O中，OA=OB=OC在四边形OABC中，有OA=OB=OC,则可以构造以O为圆心的，OA为半径的圆O。一、利用圆的定义来构造圆总结：例题中存在如图所示的一个结构，即有公共端点的三条相等线段，不妨形象地称为“相等三爪图”，它“逼”我们联想到：“到定点的距离等于定长的点的集合是圆”。见“相等三爪图”现“定义圆”二、利用90°的圆周角所对弦是直径构造圆在圆直径，点O中，AB是圆O的则有C=90°∠C在圆上，在三角形则可以ABABC为直径构造圆。中，∠C=90°总结：斜边长为定值的直角三角形，让我们联想到“90°的圆周角所对弦是直径”。我们便可以这条斜边为直径，作出该直角三角形的外接圆。见“斜边长一定的直角三角形”现“其外接圆”二、利用90°的圆周角所对弦是直径构造圆三、利用圆内接四边形对角互补构造“四点共圆”在圆O内接四边形中，四边形ACBD中，若则可以构造ACBD四点共圆。四边形ABCD中，若∠A+∠C=180°则也可以构造ABCD四点共圆。∠C=∠D=90°∠C=∠D=90°∠CAD+∠CBD=180°总结：在一个四边形中，如果有一组对角互补，那么这个四边形的四个顶点共圆。即“对角互补存隐圆”。见“四边形对角互补”现“四点共圆”三、利用对角互补型四边形“四点共圆”构造圆构造辅圆几种常见模型模型一：利用圆的定义来构造圆模型二：利用所对弦是直径构造圆90°的圆周角模型三：利用“四点共圆”构造辅助圆课堂小结化隐为显谢谢聆听！