中考专题--对角互补模型,对角互补模型总结

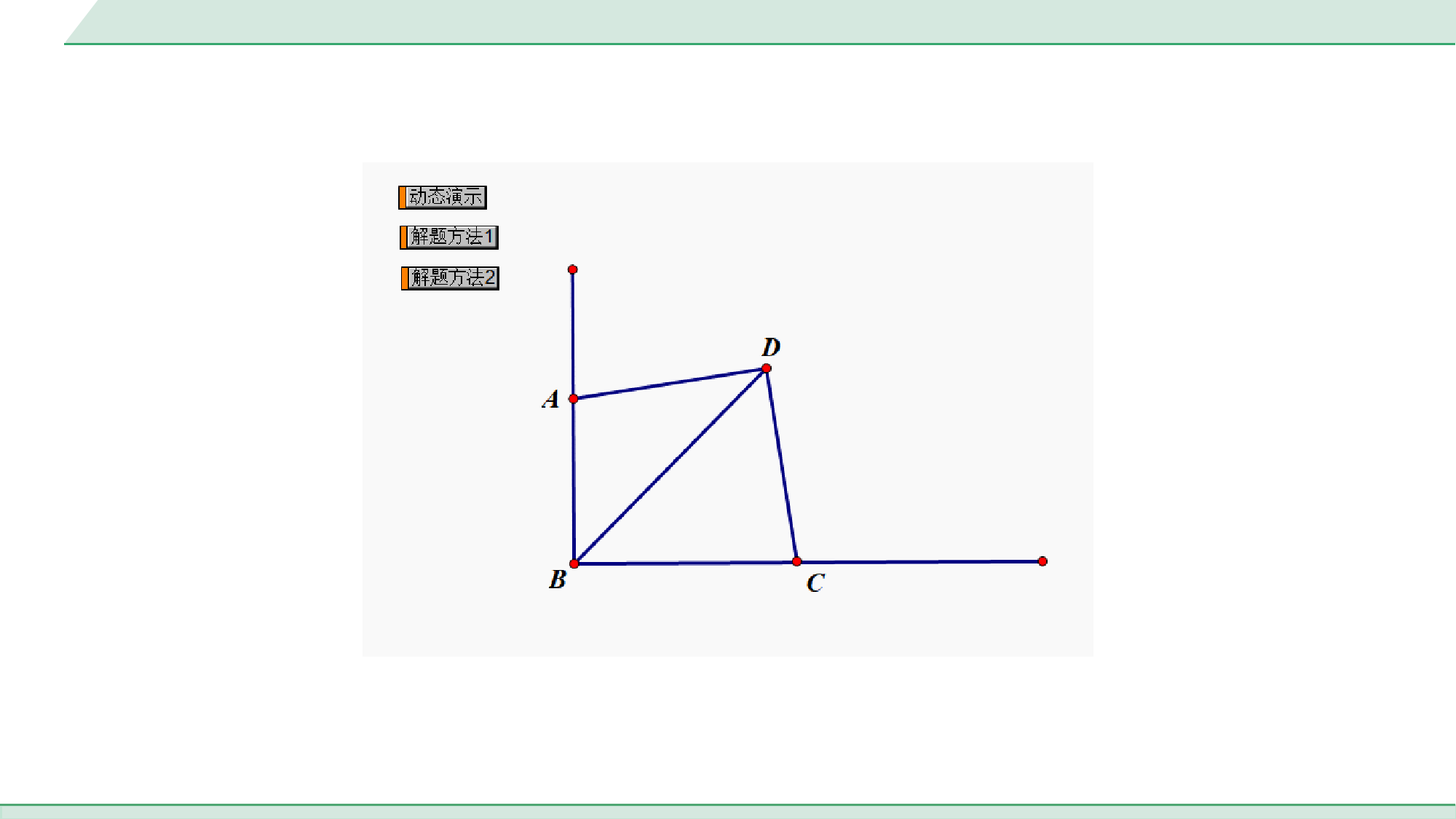
满分技法【活动目的】运用所学的知识探究对角互补模型的特点．活动1——探究对角互补90°模型【分析图形】如图①，已知∠ABC＝∠ADC＝90°，BD平分∠ABC.图①中考专题对角互补模型满分技法【提出问题】请证明以下结论是否成立：①AD＝CD；②AB＋BC＝BD；【解决问题】【方法一】过点D作垂线．2解：如解图①，过点D作DE⊥BA，DF⊥BC，垂足分别为E，F，EF∴∠DEA＝∠DFC＝90°，∵∠ABC＝90°，∴四边形BEDF是矩形，图①2∵BD平分∠ABC，∴DE＝DF，∴四边形BEDF是正方形，∵∠ADC＝90°∴∠EDA＋∠ADF＝∠ADF＋∠FDC＝90°，∴∠EDA＝∠FDC，在△ADE和△CDF中，,AEDCFDDEDFEDAFDC∴△ADE≌△CDF(ASA)，EF图①,AEDCFDDEDFEDAFDC∴AE＝CF，AD＝CD，∴结论①成立；∵四边形BEDF是正方形，∴BE＝BF＝BD，∵AB＋BC＝AB＋BF＋CF＝AB＋BF＋AE＝BE＋BF＝2BE，∴AB＋BC＝2×BD＝BD.∴结论②成立．22222EF图①22222∵BD平分∠ABC，∠ABC＝90°，∴∠ABD＝∠DBC＝45°，∵∠BDE＝90°，∴∠DEB＝∠ABD＝∠DBC＝45°，∴BD＝DE，∵∠ADC＝∠BDE＝90°，∴∠ADB＋∠BDC＝∠BDC＋∠CDE，∴∠ADB＝∠CDE，【方法二】以点D为垂足作垂线．E解：过点D作DE⊥BD，交BC的延长线于点E，连接DE.图①在△ABD和△CED中，,ADBCDEBDEDABDCED∴△ABD≌△CED(ASA)，∴AB＝CE，AD＝CD，∴结论①成立；∴AB＋BC＝CE＋BC＝BE，∵在Rt△BDE中，BE＝BD，22E图①,ADBCDEBDEDABDCED22满分技法活动2——探究对角互补60°和120°模型【分析图形】如图②，已知∠ABC＝2∠ADC＝120°，BD平分∠ABC.图②满分技法【提出问题】请证明以下结论是否成立：①AD＝CD；②AB＋BC＝BD；【解决问题】图②【方法一】解：如解图③，过点D作DE⊥BA，交BA的延长线于点E，DF⊥BC于点F，EF∴∠AED＝∠CFD＝90°，∵BD平分∠ABC，∴DE＝DF，在四边形BFDE中，满分技法∵∠ABC＝120°，∴∠EDF＝60°，∴∠EDA＋∠ADF＝60°，∵2∠ADC＝120°，∴∠ADC＝60°，∴∠ADF＋∠FDC＝60°，∴∠EDA＝∠FDC，在△DEA和△DFC中，,EDAFDCDEDFAEDCFD∴△DEA≌△DFC(ASA)，∴AE＝CF，AD＝CD，图②EF,EDAFDCDEDFAEDCFD∴结论①成立，在Rt△BDE中，∵∠DBE＝60°，∴BE＝BD，∴AB＋BC＝AB＋BF＋CF＝AB＋BF＋AE＝BE＋BF，易知△BED≌△BFD，∴BE＝BF，∴AB＋BC＝2BE＝2×BD＝BD，∴AB＋BC＝BD.∴结论②成立．1212图②EF1212∵∠ABC＝120°，BD平分∠ABC，∴∠ABD＝∠DBE＝60°，又∵∠BDE＝60°∴△BDE是等边三角形，∴BD＝DE，∠BDE＝∠BED＝∠ABD＝60°，∴∠BDC＋∠CDE＝60°，【方法二】解：如解图④，以BD为边作∠BDE＝60°，交BC的延长线于点E.解图④∴∠ADB＝∠CDE，在△ABD和△CED中，,ADBCDEBDDEABDCED∴△ABD≌△CED(ASA)，∴AB＝CE，AD＝CD，∴结论①成立，∴AB＋BC＝CE＋BC＝BE＝BD.∴结论②成立．解图④,ADBCDEBDDEABDCED满分技法活动3——类比探究【提出问题】如图③，已知∠ABC＝∠ADC＝90°，∠CBD＝α.求证：CD＝AD·tanα.【解决问题】图③证明：如解图⑤，过点D分别作DE⊥AB，DF⊥BC分别交AB于点E，交BC于点F.图③EF由题易证，△ADE∽△CDF，∴，∵DE＝BF，∴在Rt△BDF中，tanα＝，∴tanα＝，∴CD＝AD·tanα.CDDFADDEDFDFBFDECDADCDDFADDEDFDFBFDECDAD满分技法【真题再现】1.(1)【探究发现】如图①，∠EOF的顶点O在正方形ABCD两条对角线的交点处，∠EOF＝90°，将∠EOF绕点O旋转，旋转过程中，∠EOF的两边分别与正方形ABCD的边BC和CD交于点E和点F(点F与点C，D不重合)．则CE，CF，BC之间满足的数量关系是________；第1题图①【解法提示】∵四边形ABCD是正方形，∴AC⊥BD，OB＝OC，∠OBE＝∠OCF＝45°，∵∠EOF＝∠BOC＝90°，∴∠BOE＋∠EOC＝∠EOC＋∠COF，∴∠BOE＝∠COF，∴△BOE△COF(ASA)，∴BE＝CF，∴CE＋CF＝CE＋BE＝BC.解：(1)CE＋CF＝BC；第1题图①满分技法(2)【类比应用】如图②，若将(1)中的“正方形ABCD”改为“∠BCD＝120°的菱形ABCD”，其他条件不变，当∠EOF＝60°时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由；第1题图②满分技法理由：如解图①，连接EF，在CO上截取CJ＝CF，连接FJ.(2)(1)中结论不成立．猜想结论：CE＋CF＝BC.12J∵四边形ABCD是菱形，∠BCD＝120°，∴∠BCO＝∠OCF＝60°，∴∠OBC＝30°，∴OC＝BC.∵∠EOF＋∠ECF＝180°，∴O，E，C，F四点共圆，∴∠OFE＝∠OCE＝60°，12第1题图②1212∵∠EOF＝60°，∴△EOF是等边三角形，∴OF＝FE，∠OFE＝60°，∵CF＝CJ，∠FCJ＝60°，∴△CFJ是等边三角形，∴FC＝FJ，∠JFC＝∠OFE＝60°，∴∠OFJ＝∠CFE，∴△OFJ≌△EFC(SAS)，∴OJ＝EC，∴CF＋CE＝CJ＋OJ＝OC＝BC；12J第1题图②12满分技法(3)【拓展延伸】如图③，∠BOD＝120°，OD＝，OB＝4，OA平分∠BOD，AB＝，且OB＞2OA，点C是OB上一点，∠CAD＝60°，求OC的长．3413第1题图③3413(3)如解图②，由OB＞2OA可知△BAO是钝角三角形，∠BAO＞90°，过点A作AH⊥OB于点H，设OH＝x.H在Rt△AHO中，∵OA平分∠BOD，∴∠HOA＝∠BOD＝60°，∴AH＝x，在Rt△ABH中，BH＝，∵OB＝4，∴＋x＝4，解得x＝或，122133x2133x32123第1题图③122133x2133x32123∴OH＝或(舍去)，∴OA＝2OH＝1，∵∠COD＋∠CAD＝180°，∴A，C，O，D四点共圆，∵OA平分∠COD，∴∠AOC＝∠AOD＝60°，∴∠ADC＝∠AOC＝60°，∵∠CAD＝60°，∴△ACD是等边三角形，由(2)得OC＋OD＝OA，32123414H第1题图③32123414