面板数据模型,面板数据模型是什么意思

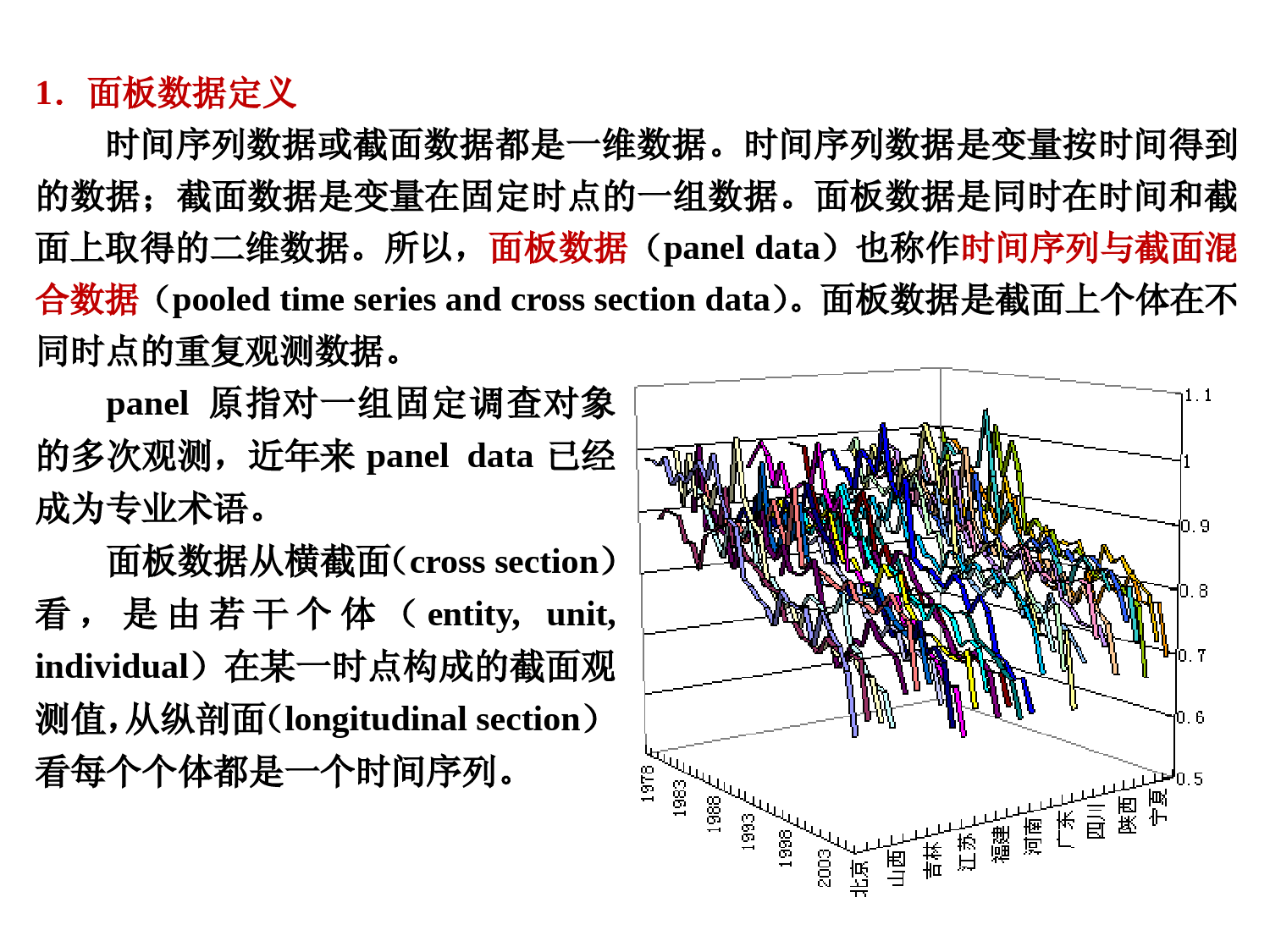
第4章面板数据模型南开大学数量经济研究所所长数量经济学专业博士生导师张晓峒nkeviews@yahoo.com.cnfile：5panel02file：6panel02file：5panel02a4.1面板数据定义4.2面板数据模型分类4.3面板数据模型估计方法4.4面板数据模型的检验与设定4.5面板数据建模案例分析4.6面板数据的其他模型4.7EViews操作第第44章面板数据模型章面板数据模型ChengHsiaoChengHsiaoBaltagi《面板数据的计量经济分析》白仲林著，张晓峒主审，南开大学出版社，2008，书号ISBN978-7-310-02915-0白仲林著Baltagi著白仲林主译1．面板数据定义时间序列数据或截面数据都是一维数据。时间序列数据是变量按时间得到的数据；截面数据是变量在固定时点的一组数据。面板数据是同时在时间和截面上取得的二维数据。所以，面板数据（paneldata）也称作时间序列与截面混合数据（pooledtimeseriesandcrosssectiondata）。面板数据是截面上个体在不同时点的重复观测数据。panel原指对一组固定调查对象的多次观测，近年来paneldata已经成为专业术语。面板数据从横截面（crosssection）看，是由若干个体（entity,unit,individual）在某一时点构成的截面观测值，从纵剖面（longitudinalsection）看每个个体都是一个时间序列。1．面板数据定义面板数据分两种特征：（1）个体数少，时间长。（2）个体数多，时间短。面板数据主要指后一种情形。面板数据用双下标变量表示。例如yit,i=1,2,…,N;t=1,2,…,Ti对应面板数据中不同个体。N表示面板数据中含有N个个体。t对应面板数据中不同时点。T表示时间序列的最大长度。若固定t不变，yi.,(i=1,2,…,N)是横截面上的N个随机变量；若固定i不变，y.t,(t=1,2,…,T)是纵剖面上的一个时间序列（个体）。对于面板数据yit,i=1,2,…,N;t=1,2,…,T，如果每个个体在相同的时期内都有观测值记录，则称此面板数据为平衡面板数据（balancedpaneldata）。若面板数据中的个体在相同时期内缺失若干个观测值，则称此面板数据为非平衡面板数据（unbalancedpaneldata）。利用面板数据建立模型的好处是：（1）由于观测值的增多，可以增加估计量的抽样精度。（2）对于固定效应模型能得到参数的一致估计量，甚至有效估计量。（3）面板数据建模比单截面数据建模可以获得更多的动态信息。安徽河北江苏内蒙古山西1996199920020200040006000800010000120001400019961997199819992000200120021996199820002002安徽福建黑龙江江苏辽宁山东山西浙江02000400060008000100001200014000安徽北京福建河北黑龙江吉林江苏江西辽宁内蒙古山东上海山西天津浙江安徽河北江苏内蒙古山西19961998200020020200040006000800010000120001996199719981999200020012002199619992002安徽河北江苏内蒙古山西020004000600080001000012000安徽北京福建河北黑龙江吉林江苏江西辽宁内蒙古山东上海山西天津浙江案例1（file:5panel02）：1996-2002年中国东北、华北、华东15个省级地区的居民家庭固定价格的人均消费（CP）和人均收入（IP）数据。数据是7年的，每一年都有15个数据，共105组观测值。人均消费和收入两个面板数据都是平衡面板数据，各有15个个体。面板数据散点图15个地区7年人均消费对收入的面板数据散点图见图6和图7。图6中每一种符号代表一个年度的截面散点图（共7个截面）。相当于观察7个截面散点图的叠加。图7中每一种符号代表一个省级地区的7个观测点组成的时间序列。相当于观察15个时间序列。图图66图图772,0003,0004,0005,0006,0007,0008,0009,00010,00011,0003,0005,0007,0009,00011,00013,000CP_1996CP_1997CP_1998CP_1999CP_2000CP_2001CP_2002IP2,0003,0004,0005,0006,0007,0008,0009,00010,00011,0003,0005,0007,0009,00011,00013,000CP_IAHCP_IBJCP_IFJCP_IHBCP_IHLJCP_IJLCP_IJSCP_IJXCP_ILNCP_INMGCP_ISDCP_ISHCP_ISXCP_ITJCP_IZJIP5panel02a5panel02aFileFile：：5panel02a5panel02a2000300040005000600070008000900010000110002000400060008000100001200014000IPCROSSCP1996CP1997CP1998CP1999CP2000CP2001CP2002IP用原变量建模还是用对数变量建模?7.88.08.28.48.68.89.09.29.48.08.28.48.68.89.09.29.49.6LOG(IPCROSS)LOG(CP1996)LOG(CP1997)LOG(CP1998)LOG(CP1999)LOG(CP2000)LOG(CP2001)LOG(CP2002)人均消费对收入的面板数据散点图对数的人均消费对收入的面板数人均消费对收入的面板数据散点图对数的人均消费对收入的面板数据散点图据散点图本例用对数数据研究更合理本例用对数数据研究更合理为了观察得更清楚，图8给出北京和内蒙古1996-2002年消费对收入散点图。从图中可以看出，无论是从收入还是从消费看内蒙古的水平都低于北京市。内蒙古2002年的收入与消费规模还不如北京市1996年的大。图9给出该15个省级地区1996和2002年的消费对收入散点图。6年之后15个地区的消费和收入都有了相应的提高。2000300040005000600070008000900010000110002000400060008000100001200014000cp_bjcp_nmgIP_I2000300040005000600070008000900010000110002000400060008000100001200014000CP_1996CP_2002IP_T图图88图图99尽管两个地区的水平值差异很大，但消费结构并没有太大的变化。尽管两个地区的水平值差异很大，但消费结构并没有太大的变化。2．面板数据模型分类用面板数据建立的模型通常有3种，即混合模型、固定效应模型和随机效应模型。2.1混合模型（Pooledmodel）。如果一个面板数据模型定义为，yit=+Xit'+it,i=1,2,…,N;t=1,2,…,T(1)其中yit为被回归变量（标量），表示截距项，Xit为k1阶回归变量列向量（包括k个回归量），为k1阶回归系数列向量，it为误差项（标量）。则称此模型为混合模型。混合模型的特点是无论对任何个体和截面，回归系数和都相同。如果模型是正确设定的，解释变量与误差项不相关，即Cov(Xit,it)=0。那么无论是N，还是T，模型参数的混合最小二乘估计量（PooledOLS）都是一致估计量。以案例1（file:5panel02）为例得到的混合模型估计结果如下：LnCPit=0.0187+0.9694LnIPit+it(0.2)(79.2)R2=0.984,SSE=0.1702,DW=0.62人均消费对人均可支配收入的弹性系数人均消费对人均可支配收入的弹性系数是是0.96940.9694。。人均消费对人均可支配收入的边际系人均消费对人均可支配收入的边际系数是数是0.96940.9694CPCPitit//IPIPitit2.2固定效应模型（fixedeffectsmodel）。固定效应模型分为3种类型，即个体固定效应模型、时点固定效应模型和个体时点双固定效应模型。下面分别介绍。2.2.1个体固定效应模型（entityfixedeffectsmodel）如果一个面板数据模型定义为，yit=i+Xit'+it,i=1,2,…,N;t=1,2,…,T(3)其中i表示对于i个个体有i个不同的截距项，Xit为k1阶回归变量列向量（包括k个回归量），为k1阶回归系数列向量，对于不同个体回归系数相同，yit为被回归变量（标量），it为误差项（标量）。如果i是随机变量，且其变化与Xit有关系，则称此模型为个体固定效应模型。个体固定效应模型（3）的强假定条件是，E(iti,Xit)=0,i=1,2,…,Ni作为随机变量描述不同个体建立的模型间的差异。i是不可观测的。第第44章面板数据模型章面板数据模型2．面板数据模型分类2.2.1个体固定效应模型（entityfixedeffectsmodel）个体固定效应模型也可以表示为yit=1D1+2D2+…+NDN+Xit'+it,t=1,2,…,T(4)其中Di=其他,,个个体如果属于第，,0...,,2,1,1Nii个体固定效应模型（3）还可以用多方程表示为y1t=1+X1t'+1t,i=1（对于第1个个体或时间序列），t=1,2,…,Ty2t=2+X2t'+2t,i=2（对于第2个个体或时间序列），t=1,2,…,T…yNt=N+XNt'+Nt,i=N（对于第N个个体或时间序列），t=1,2,…,T注意：（1）在EViews输出结果中i是以一个不变的常数部分和随个体变化的部分相加而成。（2）在EViews5.0以上版本个体固定效应对话框中的回归因子选项中填不填c输出结果都会有固定常数项。2.2.1个体固定效应模型（entityfixedeffectsmodel）对于个体固定效应模型，个体效应i未知，E(iXit)随Xit而变化，但不知怎样与Xit变化，所以E(yitXit)不可识别。对于短期面板数据，个体固定效应模型是正确设定的，的混合OLS估计量不具有一致性。下面解释设定个体固定效应模型的原因。假定有面板数据模型yit=0+1xit+2zi+it,i=1,2,…,N;t=1,2,…,T(5)其中0为常数，不随时间、截面变化；zi表示随个体变化，但不随时间变化的难以观测的变量。令i=0+2zi，于是（5）式变为yit=i+1xit+it,i=1,2,…,N;t=1,2,…,T(6)上模型可以被解释为含有N个截距，即每个个体都对应一个不同截距的模型。对于每个个体回归函数的斜率相同（都是1），这正是个体固定效应模型形式。第第44章面板数据模型章面板数据模型2.2.1个体固定效应模型（entityfixedeffectsmodel）yit=i+1xit+it,i=1,2,…,N;t=1,2,…,T(6)上模型可以被解释为含有N个截距，即每个个体都对应一个不同截距的模型。对于每个个体回归函数的斜率相同（都是1），这正是个体固定效应模型形式。可见个体固定效应模型中的截距项i中包括了那些随个体变化，但不随时间变化的难以观测的变量的影响。i是一个随机变量。因为zi是不随时间变化的量，所以当对个体固定效应模型中的变量进行差分时，可以剔除那些随个体变化，但不随时间变化的难以观测变量的影响，即剔出i的影响。以案例1为例，省家庭平均人口数就是这样的一个变量。对于短期面板来说，这是一个基本不随时间变化的量，但是对于不同的省份，这个变量的值是不同的。第第44章面板数据模型章面板数据模型以案例1（file:5panel02）为例得到的个体固定效应模型估计结果如下：输出结果的方程形式是tLncp1=ˆ安徽+1ˆLnip1t=(0.6878–0.0039)+0.89Lnip1t(5.4)(60.6)tLncp2=ˆ北京+1ˆLnip2t=(0.6878+0.0821)+0.89Lnip2t(5.4)(60.6)。。。tLncp15=ˆ浙江+1ˆLnip15t=(0.6878+0.0434)+0.89Lnip15t(5.4)(60.6)R2=0.9937,SSEr=0.0667,t0.05(89)=1.98,DW=1.51从结果看，北京、上海、浙江是自发消费（消费函数截距）最大的3个地区。第第44章面板数据模型章面板数据模型2．面板数据模型分类2.2.2时点固定效应模型（timefixedeffectsmodel）如果一个面板数据模型定义为，yit=t+Xit'+it,i=1,2,…,N(7)其中t是模型截距项，随机变量，表示对于T个截面有T个不同的截距项，且其变化与Xit有关系；yit为被回归变量（标量），it为误差项（标量），满足通常假定条件。Xit为k1阶回归变量列向量（包括k个回归变量），为k1阶回归系数列向量，则称此模型为时点固定效应模型。时点固定效应模型也可以加入虚拟变量表示为yit=0+1W1+2W2+…+TWT+Xit'+it,i=1,2,…,N;t=1,2,…,T(8)其中Wt=,0;...,,2,1,1)(。，个截面不属于第其他个截面如果属于第ttTt第第44章面板数据模型章面板数据模型2.2.2时点固定效应模型（timefixedeffectsmodel）模型（8）还也可以用多方程表示为yi1=(0+1)+X1t'+i1,t=1，（对于第1个截面），i=1,2,…,Nyi2=(0+2)+X2t'+i2,t=2，（对于第2个截面），i=1,2,…,N…yiT=(0+T)+XNt'+iT,t=T，（对于第T个截面），i=1,2,…,N设定时点固定效应模型的原因。假定有面板数据模型yit=0+1xit+2zt+it,i=1,2,…,N;t=1,2,…,T(9)其中0为常数，不随时间、截面变化；zt表示随不同截面（时点）变化，但不随个体变化的难以观测的变量。令t=0+2zt，于是（9）式变为yit=t+1xit+it,i=1,2,…,N;t=1,2,…,T(10)上述模型可以被解释为含有T个截距，即每个截面都对应一个不同截距的模型。这正是时点固定效应模型形式。对于每个截面，回归函数的斜率相同（都是1），t却因截面（时点）不同而异。可见时点固定效应模型中的截距项t包括了那些随不同截面（时点）变化，但不随个体变化的难以观测的变量的影响。t是一个随机变量。以案例1为例，“全国零售物价指数”就是这样的一个变量。对于不同时点，这是一个变化的量，但是对于不同省份（个体），这是一个不变化的量。以例1为例得到的时点固定效应模型估计结果1iLncp=ˆ0+ˆ1996+1ˆLnipi1=(-0.2474+0.0257)+1.00Lnipi1,t=1996(-2.1)(72.9)2iLncp=ˆ0+ˆ1997+1ˆLnipi2=(-0.2474+0.0266)+1.00Lnipi2,t=1997(-2.1)(72.9)…7iLncp=ˆ0+ˆ2002+1ˆLnipi7=(-0.2474–0.0204)+1.00Lnipi7,t=2002(-2.1)(72.9)R2=0.9867,SSEr=4028843,t0.05(97)=1.98注意：时点固定效应模型中不可以加AR项。第第44章面板数据模型章面板数据模型2．面板数据模型分类2.2.3个体时点固定效应模型（timeandentityfixedeffectsmodel）如果一个面板数据模型定义为，yit=0+i+t+Xit'+it,i=1,2,…,N;t=1,2,…,T(11)其中yit为被回归变量（标量）；i是随机变量，表示对于N个个体有N个不同的截距项，且其变化与Xit有关系；t是随机变量，表示对于T个截面（时点）有T个不同的截距项，且其变化与Xit有关系；Xit为k1阶回归变量列向量（包括k个回归量）；为k1阶回归系数列向量；it为误差项（标量）满足通常假定(itXit,i,t)=0；则称此模型为个体时点固定效应模型。个体时点固定效应模型还可以表示为，yit=0+1D1+2D2+…+NDN+1W1+2W2+…+TWT+Xit'+it,(12)其中Di=其他,,个个体如果属于第，,0...,,2,1,1NiiWt=)(,0;,...,2,1,1。个截面不属于第其他个截面，如果属于第tTtt如果模型形式是正确设定的，并且满足模型通常的假定条件，对模型（12）进行混合OLS估计，全部参数估计量都是不一致的。正如个体固定效应模型可以得到一致的、甚至有效的估计量一样，一些计算方法也可以使个体时点双固定效应模型得到更有效的参数估计量。以例1为例得到的截面、时点固定效应模型估计结果如下：注意：（1）对于第1个截面（t=1）EViwes输出结果中把(1+i),(i=1,2,…,N)写在一起。（2）对于第2,…,T个截面（t=1）EViwes输出结果中分别把(t+i),(t=2,…,T),(i=1,2,…,N)估计在一起。2．面板数据模型分类2.2.3个体时点固定效应模型（timeandentityfixedeffectsmodel）输出结果如下：1996,1Lncp=ˆ0+ˆ1+ˆ1996+1ˆLnip1,1996=2.40-0.04-0.06+0.70Lnip1,1996（安徽省）1996,2Lncp=ˆ0+ˆ2+ˆ1996+1ˆLnip2,1996=2.40+0.17–0.06+0.70Lnip2,1996（北京市）…1997,1Lncp=ˆ0+ˆ1+ˆ1997+1ˆLnip1,1997=2.40–0.04+0.02+0.70Lnip1,1997（安徽省）1997,2Lncp=ˆ0+ˆ2+ˆ1997+1ˆLnip2,1997=2.40+0.17+0.02+0.70Lnip2,1997（北京市）…2002,15Lncp=ˆ0+ˆ15+ˆ2002+1ˆLnip15,2002=2.40+0.12+0.06+0.70Lnip15,2002（浙江省）R2=0.9947,SSEr=0.0562,t0.05(83)=1.98注意：（1）个体时点固定效应模型中不可以加AR项。（2）在上述三种固定效应模型中，个体固定效应模型最为常用。2．面板数据模型分类2.3随机效应模型对于面板数据模型yit=i+Xit'+it,i=1,2,…,N;t=1,2,…,T(15)如果i为随机变量，其分布与Xit无关；Xit为k1阶回归变量列向量（包括k个回归量），为k1阶回归系数列向量，对于不同个体回归系数相同，yit为被回归变量（标量），it为误差项（标量），这种模型称为个体随机效应模型（随机截距模型、随机分量模型）。其假定条件是iiid(,2)itiid(0,2)都被假定为独立同分布，但并未限定何种分布。同理也可定义时点随机效应模型和个体时点随机效应模型，但个体随机效应模型最为常用。对于个体随机效应模型，E(iXit)=，则有，E(yitxit)=+Xit'，对yit可以识别。所以随机效应模型参数的混合OLS估计量具有一致性，但不具有有效性。第第44章面板数据模型章面板数据模型例1的个体随机效应模型估计结果如下：注意：术语“随机效应模型”和“固定效应模型”用得并不十分恰当，容易产生误解。其实固定效应模型应该称之为“相关效应模型”，而随机效应模型应该称之为“非相关效应模型”。因为固定效应模型和随机效应模型中的i都是随机变量。3.面板数据模型估计方法3.1混合最小二乘（PooledOLS）估计（适用于混合模型）3.2平均数（between，组间）OLS估计（适用于混合模型、个体随机效应模型）3.3离差变换（within，组内）OLS估计（适用于个体固定效应模型）3.4一阶差分（firstdifference）OLS估计（适用于个体固定效应模型）3.5随机效应（randomeffects）估计法（可行GLS（feasibleGLS）估计法）（适用于个体随机效应模型）3．面板数据模型估计方法面板数据模型中的估计量既不同于截面数据估计量，也不同于时间序列估计量，其性质随设定固定效应模型是否正确而变化。回归变量xit可以是时变的，也可以是非时变的。3.1混合最小二乘（PooledOLS）估计混合OLS估计方法是在时间上和截面上把NT个观测值混合在一起，然后用OLS法估计模型参数。给定混合模型yit=+Xit'+it,i=1,2,…,N;t=1,2,…,T(19)把上模型写成向量形式，uWγy其中y=(y1…yN)和u=(u1…uN)是NT1阶列向量。=()(k+1)1列向量。W=(1Xit)NT(k+1)阶矩阵，其第1列是单位列向量。假定条件是E(u∣W)=0，误差项u是严格外生的。E(uu∣W)=，则的混合OLS估计公式是γˆ(WW)-1Wy第第44章面板数据模型章面板数据模型3．面板数据模型估计方法3.1混合最小二乘（PooledOLS）估计如果模型是正确设定的，且解释变量与误差项不相关，即Cov(Xit,it)=0。那么无论是N，还是T，模型参数的混合最小二乘估计量都具有一致性。对混合模型通常采用的是混合最小二乘（PooledOLS）估计法。然而，在误差项服从独立同分布条件下由OLS法得到的方差协方差矩阵，在这里通常不会成立。因为对于每个个体i及其误差项来说通常是序列相关的。NT个相关观测值要比NT个相互独立的观测值包含的信息少。从而导致误差项的标准差常常被低估，估计量的精度被虚假夸大。如果模型存在个体固定效应，即i与Xit相关，那么对模型应用混合OLS估计方法，估计量不再具有一致性。解释如下：假定模型实为个体固定效应模型yit=i+Xit'+it，但却当作混合模型来估计参数，则模型可写为yit=+Xit'+(i-+it)=+Xit'+uit(20)其中uit=(i-+it)。因为i与Xit相关，也即uit与Xit相关，所以个体固定效应模型的参数若采用混合OLS估计，估计量不具有一致性。3.2平均数（between）OLS估计平均数OLS估计法的步骤是首先对面板数据中的每个个体求平均数，共得到N个平均数（估计值）。然后利用yit和Xit的N组观测值估计参数。以个体固定效应模型yit=i+Xit'+it(21)为例，首先对面板中的每个个体求平均数，从而建立模型iy=i+iX'+i,i=1,2,…,N(22)其中iy=TtityT11，iX=TtitT11X，i=TtitT11，i=1,2,…,N。变换（22）式如下iy=+iX'+(i-+i),i=1,2,…,N(23)上式称作平均数模型。对上式应用OLS估计，则参数估计量称作平均数OLS估计量。此条件下的样本容量为N。由于i和Xit相关，也即i和iX相关，所以，回归参数的平均数OLS估计量是非一致估计量。对于混合模型yit=+Xit'+it，如果it和Xit不相关，也即it和iX不相关，则和的平均数OLS估计量是一致估计量。平均数OLS估计法适用于短期面板的混合模型和个体随机效应模型。3.3离差变换（within）OLS估计对于短期面板数据，离差变换OLS估计法的原理是先把面板数据中每个个体的观测值变换为对其平均数的离差观测值，然后利用离差变换数据估计模型参数。具体步骤是，对于个体固定效应模型yit=i+Xit'+it(24)中的每个个体计算平均数，可得到如下模型，iy=i+iX'+i上两式相减，消去了i，得yit-iy=(Xit-iX)'+(it-i)此模型称作离差变换数据模型。对上式应用OLS估计，ˆ=NiTtNiTtiityy1111))(())((iitiitiitXXXXXX所得的估计量称作离差变换OLS估计量。对于个体固定效应模型，的离差变换OLS估计量是一致估计量。如果it还满足独立同分布条件，的离差变换OLS估计量不但具有一致性还具有有效性。4.3.3离差变换（within）OLS估计如果对固定效应i感兴趣，可按下式估计。iˆ=iy-iX'ˆ,i=1,2,…,N(27)利用中心化（或离差变换）数据，计算回归参数估计量ˆ的方差协方差矩阵如下，Var(ˆ)=2ˆ111))((NiTtiitiitXXXX，其中2ˆ=kNNTNiTtit112ˆ。个体固定效应模型的估计通常采用的就是离差变换（within）OLS估计法。当个体数N不大时，可采用OLS虚拟变量估计法估计i和。在短期面板条件下，即便i的分布、以及i和Xit的关系都已知到，i的估计量仍不具有一致性。方差分析方差分析SA=kimjiXX112)(=kiiXXm12)(称样本组间（between）离差平方和SE=kimjiijXX112)(称样本组内（within）离差平方和其中iX表示各个水平的样本平均数，X表示样本总平均数。批号验结果i…j…m行平均均值水平A1X11…X1j…X1m1X1………AiXi1…Xij…XimiXi…………AkXk1…Xkj…XkmkXkkXNXiij)(=X（km=N）3．面板数据模型估计方法3.4一阶差分（firstdifference）OLS估计在短期面板条件下，一阶差分OLS估计就是对个体固定效应模型中的回归量与被回归量的差分变量构成的模型的参数进行OLS估计。具体步骤是，对个体固定效应模型yit=i+Xit'+it取其滞后一期关系式yit-1=i+Xit-1'+it-1上两式相减，得一阶差分模型（i被消去）yit-yit-1=(Xit-Xit-1)'+(it-it-1),i=1,2,…,N;t=1,2,…,T对上式应用OLS估计得到的的估计量称作一阶差分OLS估计量。尽管i不能被估计，的估计量是一致估计量。在T>2，it独立同分布条件下得到的的一阶差分OLS估计量不如离差变换OLS估计量有效。3.5随机效应（randomeffects）估计法（可行GLS（feasibleGLS）估计法）有个体随机效应模型，yit=+i+Xit'+i，其中i，it服从独立同分布，是常数。对其作如下变换yit-iyˆ=(1-ˆ)+(Xit-ˆiX)'+vit（29）其中vit=(1-ˆ)i+(it-ˆi)渐近服从独立同分布，=1-22T，应用OLS估计，则所得估计量称为随机效应估计量或可行GLS估计量。当ˆ=0时，（29）式等同于混合OLS估计；当ˆ=1时，（29）式等同于离差变换OLS估计。对于随机效应模型，可行GLS估计量不但是一致估计量，而且是有效估计量，但对于个体固定效应模型，可行GLS估计量不是一致估计量。面板数据模型估计量的稳健统计推断。在实际的经济面板数据中，N个个体之间相互独立的假定通常是成立的，但是每个个体本身却常常是序列自相关的，且存在异方差。为了得到正确的统计推断，需要克服这两个因素。对于第i个个体，当N，Xi的方差协方差矩阵仍然是TT有限阶的，所以可以用以前的方法克服异方差。采用GMM方法还可以得到更有效的估计量。EViwes中对随机效应模型的估计采用的就是可行（feasible）GLS估计法。4．面板数据模型检验与设定方法关于面板数据模型参数的约束检验介绍3个统计量。4.1面板数据模型中丢失变量或存在多余变量的F检验F=)1/(/)(kNTSSEmSSESSEuurFm,NT-k-1)其中SSEr表示施加约束条件后估计模型的残差平方和；SSEu表示未施加约束条件的估计模型的残差平方和；m表示约束条件个数；NT表示面板数据样本容量（N表示个体数，T表示个体长度）；k表示非约束面板数据模型中被估参数的个数。判别规则是，若FF0.05(14,89)=1.78，推翻原假设，比较上述两种模型，建立个体固定效应模型比混合模型更合理。EViews中称作多余的固定效应检验，使用F和LR两个统计量。在固定效应模型估计窗口中的View键选Fix/RandomEffectsTesting,RedundantFixedEffects-LikelihoodRatio功能。因为概率小于0.05，推翻原假设，两相比较，应该建立个体固定效应模型。4．面板数据模型的检验与设定4.4Hausman检验原假设与备择假设是H0:个体效应与回归变量无关（个体随机效应模型）H1:个体效应与回归变量相关（个体固定效应模型）离差变换OLS估计可行GLS估计估计量之差个体随机效应模型估计量具有一致性估计量具有一致性小个体固定效应模型估计量具有一致性估计量不具有一致性大是一个标量时，H=222~ˆ)~ˆ(SS2(1)是一个向量时，H=(ˆ-~)'[)~(Var-)ˆ(Var]-1(ˆ-~)或者H=2)~ˆ()~ˆ(22)~ˆ()~ˆ(SS2(1)H=(ˆ-~)'()~-ˆ(Var)-1(ˆ-~)2,0003,0004,0005,0006,0007,0008,0009,00010,00011,0002,0004,0006,0008,00010,00012,00014,000IPCPpooledregression7.88.08.28.48.68.89.09.29.48.08.28.48.68.89.09.29.49.6LOG(IP)LOG(CP)人均消费对收入的面板数据散点图对数的人均消费对收入的面板数据散点图5．面板数据建模案例分析案例1（file:5panel02）：1996-2002年中国东北、华北、华东15个省级地区的居民家庭固定价格的人均消费（CP）和人均收入（IP）数据见file:panel02。数据是7年的，每一年都有15个数据，共105组观测值。第第44章面板数据模型章面板数据模型5．面板数据建模案例分析个体固定效应模型估计结果如下：LnCPit=0.6878+0.8925LnIPit+it(5.4)(60.6)R2=0.99,DW=1.55．面板数据建模案例分析混合模型与个体固定效应模型比较，应该建立个体固定效应模型。F=)/(/)(kNNTSSENSSESSEuur=)214105/(0667.014/)0667.01702.0(=00075.000074.0=9.875．面板数据建模案例分析个体随机效应模型与个体固定效应模型比较，应该建立个体固定效应模型。H=2)~(2)ˆ(2)~ˆ(REWssREW=222)012976.0()014739.0()917660.0892481.0(=12.98最终确定的是建立个体固定效应模型。（5panel02）个体固定效应模型的预测。在EViews个体固定效应回归结果窗口点击Proc键，选makemodel功能，将打开一个对话窗。点击solve键。在打开的对话窗中可以选择动态预测和静态预测。图10是不带AR(1)项的个体固定效应模型对安徽省、北京市人均食品支出的样本内静态预测结果。图10不带AR(1)项的个体固定效应模型预测结果3,2003,4003,6003,8004,0004,2004,4004,6004,8001996199719981999200020012002CPAHCPAH(Baseline)5,0006,0007,0008,0009,00010,00011,0001996199719981999200020012002CPBJ(Baseline)CPBJ2,0003,0004,0005,0006,0007,0008,0009,00010,00011,0002,0004,0006,0008,00010,00012,00014,000CPAHCPAHFCPBJCPBJFCPFJCPFJFCPHBCPHBFCPHLJCPHLJFCPJLCPJLFCPJSCPJSFCPJXCPJXFCPLNCPLNFIPTIME2,0003,0004,0005,0006,0007,0008,0009,00010,00011,0002,0004,0006,0008,00010,00012,00014,000CPNMGCPNMGFCPSDCPSDFCPSHCPSHFCPSXCPSXFCPTJCPTJFCPZJCPZJFIPTIME拟合的个体回归直线拟合的个体回归直线（file：6panel02c，graph06）（file：6panel02c，graph07）5．面板数据建模案例分析案例2（file:5panel01a）美国公路交通事故死亡人数与啤酒税的关系研究见StockJHandMWWatson,IntroductiontoEconometrics,AddisonWesley,2003第8章。美国每年有4万高速公路交通事故，约1/3涉及酒后驾车。这个比率在饮酒高峰期会上升。早晨13点25%的司机饮酒。饮酒司机出交通事故数是不饮酒司机的13倍。现有19821988年48个州共336组美国公路交通事故死亡人数（number）与啤酒税（beertax）的数据。图11982年数据散点图(5panel01a-graph01)图21988年数据散点图(5panel01a-graph07)1.01.52.02.53.03.54.04.50.00.40.81.21.62.02.42.8BEER82VFR82VFR82vs.BEER821.21.62.02.42.83.23.60.00.40.81.21.62.02.4BEER88VFR88VFR88vs.BEER881982年数据的估计结果（散点图见图1）number1982=2.01+0.15beertax1982(0.15)(0.13)1988年数据的估计结果（散点图见图2）number1988=1.86+0.44beertax1988(0.11)(0.13)19821988年混合数据估计结果（file:5panel01b,散点图见图3）number19821988=1.85+0.36beertax19821988(42.5)(5.9)SSE=98.75显然以上三种估计结果都不可靠（回归参数符号不对）。原因是啤酒税之外还有许多因素（如各州的路况、车型、交通立法等因素）影响交通事故死亡人数。从面板理论上说，不知混合模型是不是最优的模型形式。0.51.01.52.02.53.03.54.04.50.00.40.81.21.62.02.42.8BEERTAXVFR图11982年数据散点图(5panel01a-graph01)图21988年数据散点图(5panel01a-graph07)1.01.52.02.53.03.54.04.50.00.40.81.21.62.02.42.8BEER82VFR82VFR82vs.BEER821.21.62.02.42.83.23.60.00.40.81.21.62.02.4BEER88VFR88VFR88vs.BEER88按个体固定效应模型估计numberit=2.375+…-0.66beertaxit(24.5)(-3.5)R2=0.91,SSE=10.35，（file:5panel01ch8-pool1,pool1）用F检验判断应该建立混合模型还是个体固定效应模型。H0：i=。混合模型（约束截距项为同一参数）。H1：i各不相同。个体固定效应模型（截距项任意取值）F=)/()1/()(kNNTSSENSSESSEuur=10.520361.08809.1)49336/(35.10)148/()35.1075.98(F0.05(47,287)=1.4因为F=52.10>F0.05(47,287)=1.4，推翻原假设，比较上述两种模型，建立个体固定效应模型更合理。为什么建立个体固定效应模型更合理？因为在进行离差变换OLS估计过程中剔除了那些影响交通事故数，但没有在模型中列出的重要解释变量。按双固定效应模型估计numberit=2.37+…-0.646beertaxit(23.3)(-3.25)SSE=9.92用F检验判断应该建立混合模型还是个体时点双固定效应模型。H0：i=。t=。混合模型（约束截距项为同一参数）。H1：i，t各不相同。个体时点双固定效应模型（截距项任意取值）F=)/()/()(kTNNTSSETNSSESSEuur=48.470353.06760.1)748336/(92.9)17148/()92.975.98(F0.05(53,281)=1.38因为F=47.48>F0.05(55,279)=1.38，推翻原假设，比较上述两种模型，建立个体时点双固定效应模型比混合模型合理。用Hausman检验判断应该建立个体随机效应模型还是个体固定效应模型。H0:个体效应与回归变量无关（个体随机效应模型）H1:个体效应与回归变量相关（个体固定效应模型）H检验的EViews输出结果如下。比较个体固定效应模型和个体随机效应模型，因为相应p值小于0.05，结论是应该建立个体固定效应模型。案例2（file:5panel01a）美国公路交通事故死亡人数与啤酒税的关系研究差分OLS估计也是估计固定效应模型的一种方法，Stock利用1988年和1982年数据的差分数据（6阶差分）得估计结果（见图4）。这个估计结果在符号上也是合理的。number1988-number1982=-0.072-1.04(beertax1988-beertax1982)(0.065)(0.36)图4差分数据散点图(File:5panel01a-graph08)-.6-.4-.2.0.2.4.6-1.6-1.2-0.8-0.40.00.40.8VFR88-VFR82BEER88-BEER82例3:加入人力资本的生产函数研究05,00010,00015,00020,00025,00030,00035,00040,00002,5005,0007,50010,00012,50015,000YBJYTJYHEBYSXCYNMGYLNYJLYHLJYSHYJSYZJYAHYFJYJXYSDYHENYHUBYHUNYGDYGXYHNYSCYGZYYNYSXYGSYQHYNXYXJK678910115.05.56.06.57.07.58.08.59.09.510.0LNYAH01LNYBJ01LNYGD01LNYGS01LNYGX01LNYGZ01LNYHEB01LNYHEN01LNYHLJ01LNYHN01LNYHUB01LNYHUN01LNYJL01LNYJS01LNYJX01LNYLN01LNYNMG01LNYNX01LNYQH01LNYSC01LNYSD01LNYSH01LNYSXC01LNYTJ01LNYXJ01LNYYN01LNYZJ01LOG(K)人均产出y对人均资本K的面板数据散点图对数形式人均产出Lny对人均资本LnK的面板数据散点图5．面板数据建模案例分析（（FileFile：：5panel05panel044））（（FileFile：：5panel045panel04aa））5．面板数据建模案例分析例3:加入人力资本的生产函数研究05,00010,00015,00020,00025,00030,00035,00040,0004567891011YAHYBJYFJYGDYGSYGXYGZYHEBYHENYHLJYHNYHUBYHUNYJLYJSYJXYLNYNMGYNXYQHYSCYSDYSHYSXYSXCYTJYXJYYNYZJEDU678910114567891011LNYAH01LNYBJ01LNYGD01LNYGS01LNYGX01LNYGZ01LNYHEB01LNYHEN01LNYHLJ01LNYHN01LNYHUB01LNYHUN01LNYJL01LNYJS01LNYJX01LNYLN01LNYNMG01LNYNX01LNYQH01LNYSC01LNYSD01LNYSH01LNYSXC01LNYTJ01LNYXJ01LNYYN01LNYZJ01EDU人均产出Lny对人均受教育时间edu的面板数据散点图对数形式人均产出Lny对人均受教育时间edu的面板数据散点图结合图形分析，建立如下计量模型:itititititu+edu+lnk+c=lny（（FileFile：：5panel05panel044））（（FileFile：：5panel045panel04aa））三．模型估计与分析（1）模型估计我们首先使用混合模型估计，估计结果如下：Lnyit=1.67+0.81Lnkit+0.08eduit+uit(1)(26.4)(58.5)(6.8)R2=0.96,DW=0.37,SSE=12.0被估参数均通过显著性检验，回归方程拟和的效果也较好，但DW值太低，存在正自相关。在混合模型中加入AR(1)后的输出结果：Lnyit=6.21+0.45Lnkit+0.05eduit+0.96AR(1)+vit(2)(8.8)(13.4)(6.8)(83.6)R2=0.99,DW=2.1,SSE=3.07AR(1)的回归参数显著的不为零，DW的值说明模型已消除了自相关。三．模型估计与分析再建立个体固定效应模型，估计结果如下：Lnyit=(1.19-0.49)+(1.19-0.17)D2+…+(1.19-0.01)D29+0.76Lnkit+0.21eduit+uit(21.7)(48.8)(11.3)R2=0.98,SSE=4.4,DW=1.06其中虚拟变量D2、D3…，D29的定义为：02932iii1其它，，，个个体，属于第如果iD模型的DW值太小，存在自相关。加入AR(1)后的个体固定效应模型估计结果如下：Lnyit=(1.65-0.34)+(1.65-0.12)D2+…+(1.65-0.23)D29+0.75Lnkit+0.16eduit+0.58AR(1)+vit(34.5)(7.9)(12.5)R2=0.99,SSE=3.2,DW=2.09其中虚拟变量D2、D3…，D29的定义为：02932iii1其它，，，个个体，属于第如果iD已消除自相关。下面用F统计量检验是应该建立混合模型还是个体固定效应模型，原假设与备择假设分别为：H0：模型中不同个体的截距相同H1：模型中不同个体的截距不同对模型(1)和(3)进行考察：7.24)2-29-432/(4.4)28/()4.4-(12.0)--/()/()-(KNNTSSE1-NSSESSEFUURF=24.7>F0.05(28,401)，所以推翻原假设。比较上述两个模型，个体固定效应模型（3）比混合模型（1）合理。接下来考察个体随机效应模型，估计结果如下：Lnyit=(1.26-0.43)+(1.26-0.15)D2+…+(1.26-0.23)D29+0.78Lnkit+0.18eduit+uit(5)(21.9)(54.0)(10.7)R2=0.98,SSE=4.9,DW=0.92,T=432其中虚拟变量D2、D3…，D29的定义为：02932iii1其它，，，个个体，属于第如果iD下面进行Hausman检验是应该建立个体随机效应模型(5)还是个体固定效应模型(3)。原假设和备择假设分别为：H0：个体随机效应模型，H1：个体固定效应模型因为H=22.4>20.05(2)=6.0，结论仍然是，模型存在个体固定效应，应该建立个体固定效应模型。案例：柯布-道格拉斯生产函数研究。Murray-book(file:5cobbdoug01)资本和劳动对产出有多大贡献一直是经济学中长期存在的一个问题。在估计生产函数时，可以得到劳动和资本贡献的一种度量指标。哈佛大学的格里历切斯（ZviGriliches）和巴黎国民统计局的马里斯（JacquesMairesse），多次利用大型的企业面板数据估计了柯布-道格拉斯生产函数。马里斯提供的面板数据包含了来自16个国家的625个企业长达8年的共5000组观测数据。0.00E+002.00E+074.00E+076.00E+078.00E+071.00E+081.20E+081.40E+080.0E+001.0E+072.0E+073.0E+074.0E+07KAPITALOUTPUT0.00E+002.00E+074.00E+076.00E+078.00E+071.00E+081.20E+081.40E+0802000006000001000000LABOROUTPUT625个企业的产出分别对资本和劳动力的散点图(file:5cobbdoug01a)案例：柯布-道格拉斯生产函数研究。Murray-book(file:5cobbdoug01)468101214161820681012141618LOGKAPLOGOUT4681012141618202468101214LOGLABORLOGOUT625个企业的对数的产出分别对对数的资本和对数的劳动力的散点图(file:5cobbdoug01a)由散点图知应该建立对数变量的模型案例：柯布-道格拉斯生产函数研究。Murray-book(file:5cobbdoug01)0.00E+005.00E+061.00E+071.50E+072.00E+072.50E+073.00E+07050000100000150000200000250000SER01SER02SER03SER04SER05SER06SER07SER08SER09SER10SER11SER12SER13SER14SER15SER16SER17SER18SER19SER20SER21SER22SER23SER24SER25SER26SER27SER28SER29LABOR020000040000060000080000010000001200000140000002000004000006000008000001000000SER01SER02SER03SER04SER05SER06SER07SER08SER09SER10SER11SER12SER13SER14SER15SER16SER17SER18SER19SER20SER21SER22SER23SER24SER25SER26SER27SER28SER29KAPITAL其中29个企业的产出分别对资本和劳动力的散点图(file:5cobbdoug01a)案例：柯布-道格拉斯生产函数研究。Murray-book(file:5cobbdoug01)681012141618681012141618LOG(SER01)LOG(SER02)LOG(SER03)LOG(SER04)LOG(SER05)LOG(SER06)LOG(SER07)LOG(SER08)LOG(SER09)LOG(SER10)LOG(SER11)LOG(SER12)LOG(SER13)LOG(SER14)LOG(SER15)LOG(SER16)LOG(SER17)LOG(SER18)LOG(SER19)LOG(SER20)LOG(SER21)LOG(SER22)LOG(SER23)LOG(SER24)LOG(SER25)LOG(SER26)LOG(SER27)LOG(SER28)LOG(SER29)LOG(KAPITAL)6810121416182468101214LOG(SER01)LOG(SER02)LOG(SER03)LOG(SER04)LOG(SER05)LOG(SER06)LOG(SER07)LOG(SER08)LOG(SER09)LOG(SER10)LOG(SER11)LOG(SER12)LOG(SER13)LOG(SER14)LOG(SER15)LOG(SER16)LOG(SER17)LOG(SER18)LOG(SER19)LOG(SER20)LOG(SER21)LOG(SER22)LOG(SER23)LOG(SER24)LOG(SER25)LOG(SER26)LOG(SER27)LOG(SER28)LOG(SER29)LOG(LABOR)其中29个企业对数的产出分别对对数的资本和劳动力的散点图(file:5cobbdoug01a)案例：柯布-道格拉斯生产函数研究。Murray-book(file:5cobbdoug01)格里历切斯（ZGriliches）和马里斯（JMairesse）给出了如下柯布-道格拉斯生产函数用对数形式估计的个体随机效应、截面固定效应的模型估计结果：120iiiiQLK资本和劳动的系数估计值0.30和0.69与我们利用美国数据得到的结果相似。输出结果还报告了个人误差成分和干扰项因观测而异的成分的方差估计值（在这种情况下，总干扰方差的93%来自于个体误差成分）。输出结果还包含了一个时间的“固定效应”；也就是说，模型中为每个年度包含了一个虚拟变量。这个年度虚拟变量就刻画了生产技术的逐年变化。案例：柯布-道格拉斯生产函数研究。Murray-book(file:5cobbdoug01)模型没有考虑不同个体之间的差异。用F检验考察个体固定效应是否有必要。检验结果显示应该建立（双）固定效应模型。豪斯曼检验结果也显示应该建立（双）固定效应模型。双固定效应估计量让我们拒绝了法国制造业企业存在着规模报酬不变的虚拟假设：尽管检验结论有所不同，但随机效应估计量和固定效应估计量所得到的β1+β2的点估计值相差不大：分别是0.99和0.97。看来，在制造业中，规模报酬非常接近于不变。双固定效应模型估计结果（1）第一自由度625-1=624，第二自由度5000-624-7-3=4366（2）第一自由度8-1=7，第二自由度5000-624-7-3=4366（3）第一自由度625-1+8-1=631，第二自由度5000-624-7-3=4366多余的个体固定效应检验豪斯曼检验结果案例7：中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？以中国29个省级地区（不包括重庆）1995-2006年间12年的面板数据对我国的经济增长与环境问题做出分析，所选数据均为平衡面板数据，共348组数据。其中，RGDP表示人均国内生产总值（单位：元），SO2表示工业二氧化硫排放量（单位：吨）。用BJ、TJ、HEB、SX、NMG、LN、JL、HLJ、SH、JS、ZJ、AH、FJ、JX、SD、HEN、HUB、HUN、GD、GX、HAN、SC、GZ、YN、SHX、GS、QH、NX、XJ分别表示北京、天津、河北、山西、内蒙古、辽宁、吉林、黑龙江、上海、江苏、浙江、安徽、福建、江西、山东、河南、湖北、湖南、广东、广西、海南、四川、贵州、云南、陕西、甘肃、青海、宁夏、新疆。（数据均来自于1996-2007年《中国统计年鉴》）。线性混合模型估计结果是SO2ij=557081.4+1.1111RGDPij（16.0）（0.4）R2=0.0005，DW=0.11,NT=2912=348说明二氧化硫排放量（SO2）与人均国内生产总值（RGDP）之间不存在线性关系。由可决系数R2=0.0005知数据一定非常散。案例7：中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？二氧化硫排放量（SO2）与人均国内生产总值（RGDP）之间是否真的不存在任何关系呢？首先看数据的散点图。040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95SO2_96SO2_97SO2_98SO2_99SO2_00SO2_01SO2_02SO2_03SO2_04SO2_05SO2_06中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？继续分析二氧化硫排放量（SO2）与人均国内生产总值（RGDP）面板数据的特征。以每个截面观测值为一种符号的面板数据散点图如下（图中把1995、2001和2006年数据分别连在一起。）：发现二氧化硫排放量（SO2）有逐年增加的趋势。040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95SO2_96SO2_97SO2_98SO2_99SO2_00SO2_01SO2_02SO2_03SO2_04SO2_05SO2_06040000080000012000001600000200000024000000100002000030000400005000060000RGDP_BJ_XJSO2_BJSO2_TJSO2_HEBSO2_SXSO2_NMGSO2_LNSO2_JLSO2_HLJSO2_SHSO2_JSSO2_ZJSO2_AHSO2_FJSO2_JXSO2_SDSO2_HENSO2_HUBSO2_HUNSO2_GDSO2_GXSO2_HANSO2_SCSO2_GZSO2_YNSO2_SHXSO2_GSSO2_QHSO2_NXSO2_XJ以每个个体观测值为一种符号的面板数据散点图如下（图中把北京、天津、上海、浙江、山东、广东和青海的数据分别连在一起）：发现北京、天津、上海二氧化硫排放量（SO2）增加的很慢，尤其是北京，呈现出逐年减少的特征。而对于其他省级地区，二氧化硫排放量（SO2）仍然呈逐年增加态势。案例7：中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？线性混合模型的回归直线和二次多项式混合模型的二次回归曲线分别见图。拟合二次回归曲线是没有道理的（人均国内生产总值超过6万元之后，二氧化硫排放量（SO2）为负）。那么应该建立何种面板数据模型呢？040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95_06SO2_95_06F1-500000050000010000001500000200000025000000100002000030000400005000060000RGDPSO2_95_06SO2_95_06vs.Polynomial(degree=2)ofRGDP第第44章面板数据模型章面板数据模型1000002000003000004000005000006000007000008000000100002000030000400005000060000so2rgdp库兹涅茨曲线(Kuznets，1955)：人均国民收入从最低上升到中等水平时，收入分配状况先趋于恶化，继而随着经济发展，逐步改善，最后达到比较公平的收入分配状况，呈颠倒过来的U的形状。GrossmanandKrueger(1991)在分析环境效应时,通过对42个国家截面数据的分析，研究了SO2、微尘和悬浮颗粒三种环境质量指标与收入之间的关系，发现环境污染与经济增长的长期关系呈倒U形，就象反映经济增长与收入分配之间关系的，并且判断出在一国人均GDP未达到40005000美元(针对SO2的分析)的转折点时，经济增长趋向于加重环境压力；一旦一国人均GDP超过了40005000美元的转折点，经济增长就开始倾向于减轻环境压力。GrossmanandKrueger用人均收入变化的两类效应来解释该现象的出现:经济发展意味着更大规模的经济活动与资源需求量,因而对环境产生负面的规模效应；但同时经济发展又通过正的技术进步效应以及结构效应减少了污染排放、改善了环境质量。这两类效应共同决定了环境质量与经济发展之间的这一倒U型曲线关系。面板数据的三次多项式混合模型拟合图（按库兹涅茨曲线假说拟合）如下：事实证明这种拟合并没有显著性。SO2ij=349806.2+41.5645RGDPij-0.00156RGDPij2+1.38108RGDPij3（4.3）（2.4）（-1.8）（1.2）R2=0.035，DW=0.12,NT=2912=348040000080000012000001600000200000024000000100002000030000400005000060000RGDPSO2_95_06SO2_95_06vs.Polynomial(degree=3)ofRGDP中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？进一步分析，看到不同个体的差异很大。可以尝试一下个体固定效应模型。个体固定效应模型估计结果：SO2ij=…+268086.1+44.9158RGDPij-0.0011RGDPij2+8.7510-9RGDPij3（6.8）（5.9）（-3.1）（1.9）R2=0.88，DW=0.91,NT=2912=348中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？选择个体固定效应模型或混合模型的F检验结果：应该建立个体固定效应模型。第第44章面板数据模型章面板数据模型中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？对个体固定效应模型加AR项克服自相关。SO2ij=…+31663.6+76.84RGDPij-0.0021RGDPij2+1.8610-8RGDPij3+0.34AR(1)（0.8）（10.7）（-6.7）（4.8）（9.6）R2=0.95，DW=1.55,NT-29=2912-29=319采用个体固定效应模型形式，倒U型曲线非常好的拟合了中国污染与人均GDP的关系。中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线。中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？29个省级地区的预测结果，0500,0001,000,0001,500,0002,000,0002,500,000010,00020,00030,00040,00050,00060,000SO2JSSO2JS_FSO2JXSO2JX_FSO2LNSO2LN_FSO2NMGSO2NMG_FSO2NXSO2NX_FSO2QHSO2QH_FSO2SCSO2SC_FSO2SDSO2SD_FSO2SHSO2SH_FSO2SHXSO2SHX_FSO2SXSO2SX_FSO2TJSO2TJ_FSO2XJSO2XJ_FSO2YNSO2YN_FSO2ZJSO2ZJ_FRGDP_TIME-200,0000200,000400,000600,000800,0001,000,0001,200,0001,400,0001,600,000010,00020,00030,00040,00050,00060,000SO2AHSO2AH_FSO2BJSO2BJ_FSO2FJSO2FJ_FSO2GDSO2GD_FSO2GSSO2GS_FSO2GXSO2GX_FSO2GZSO2GZ_FSO2HANSO2HAN_FSO2HEBSO2HEB_FSO2HENSO2HEN_FSO2HLJSO2HLJ_FSO2HUBSO2HUB_FSO2HUNSO2HUN_FSO2JLSO2JL_FRGDP_TIME15个省级地区的预测结果14个省级地区的预测结果（file：6panel03a，graph08）01234567-0.4-0.20.00.20.40.60.81.01.21.4B1F1B1F2B1F3T=20T=50T=200动态模型动态模型y=.8y(-1)+vy=.8y(-1)+v，样本容量分别为，样本容量分别为T=20T=20，，5050，，100100时，各模拟时，各模拟22万次万次6．面板数据的其他模型（动态面板数据模型、变系数面板数据模型、面板数据的向量自回归模型，非均衡面板数据模型、离散面板数据模型）6.1动态面板数据模型个体固定效应动态面板数据模型如下：yit=i+yit-1+Xit'+it,i=1,2,…,N;t=1,2,…,T以例1为例，个体固定效应动态面板数据模型估计结果itLncp=…+0.6870+0.1413Lncpit-1+0.89Lnipit(4.1)(2.1)(12.5)R2=0.9942,SSEr=0.048,DW=1.78关于模型误差项的假定如个体固定效应模型。注意：动态面板数据模型的系数估计量是有偏的不一致的估计量。6．面板数据的其他模型6.2变系数面板数据模型个体变系数（斜率）面板数据模型yit=0+i+Kkkitkix1+it,i=1,2,…,N;t=1,2,…,T时点变系数（斜率）面板数据模型yit=0+t+Kkkitktx1+it,i=1,2,…,N;t=1,2,…,T回归系数不存在显著性差异。回归系数不存在显著性差异。时点变系数（斜率）面板数据模型（例1）yit=0+t+itxit+it,i=1,2,…,15;t=1,2,…,7检验时点变系数模型的斜率和截距是否分别相等。1996=1997=1998=1999=2000=2001=20021996=1997=1998=1999=000=2001=2002EViews命令：c(2)=c(3)=c(4)=c(5)=c(6)=c(7)=c(8)c(8)=c(9)=c(10)=c(11)=c(12)=c(13)=c(14)Wald检验结果如下：6.3面板数据的向量自回归模型个体固定效应的面板数据向量自回归模型（PVAR）表示如下：Yi,t=i+1Yi,t-1+2Yi,t-2+…+pYi,t-p+1Xi,t-1+…+pXi,t-p+i,t其中Yit，i=1,2,…,N;t=p+1,p+2,…,T是个体i在时点t的m1阶列向量。Xit，i=1,2,…,N;t=1,2,…,T是个体i在时点t的m1阶外生解释变量列向量。j，j，j=1,2,…,p分别是Yi,t-j和Xi,t-j的mm阶系数矩阵。模型假定条件是（1）对于任意的N和T>p+2，Yit和Xi,t是可观测的。（2）对于i=1,2,…,N;t=1,2,…,T，it~iid（0，），即it是零期望的，方差协方差矩阵为的，独立同分布的随机变量。（3）Yi,t，Xi,t和i与误差项it正交。即E(Yi,ti,t)=E(Xi,ti,t)=E(ii,t)=0，PVAR模型的估计方法是（1）先通过对模型变量差分，剔除个体固定效应项i。Yi,t=i+1Yi,t-1+2Yi,t-2+…+pYi,t-p+1Xi,t-1+…+pXi,t-p+i,t其中i=0。（2）然后对上模型采用2SLS估计方法估计模型回归系数。（3）估计i。6.4随机系数面板数据模型对于面板数据模型yit=Kkkitkitx1+it,i=1,2,…,N;t=1,2,…,T如果kit可以线性分解为kit=ktkikvu,k=1,2,…,K。其中k是常量，kiu和ktv是分别属于个体和时点的回归系数随机成分。称这种模型为随机系数面板数据模型。目前主要有两类，Swamy随机系数面板数据模型和Hsiao随机系数面板数据模型。EViews不能估计随机系数面板数据模型。第第44章面板数据模型章面板数据模型6.5离散面板数据模型包括Probit面板数据模型，logit面板数据模型，受限（censoring，truncated）因变量面板数据模型。6.6非均衡面板数据模型非均衡面板数据各类模型与相应均衡面板数据各类模型原理相同，只是对应不同的个体，样本容量T不同。给定数据时，相应确定自由度即可。EViews有专门选项估计非均衡面板数据模型。6.7带有AR项的面板数据模型yit=i+Xit'+AR(1)+it,i=1,2,…,N;t=1,2,…,T例（file:5panel03）：中国工业污染（SO2排放量）与人均GDP的关系符合库兹涅茨曲线吗？SO2ij=…+31663.6+76.84RGDPij-0.0021RGDPij2+1.8610-8RGDPij3+0.34AR(1)（0.8）（10.7）（-6.7）（4.8）（9.6）R2=0.95，DW=1.55,NT-29=2912-29=319注意：在EViews中可以估计统一的自相关系数，也可以按个体不同各自估计自相关系数。7面板数据分析的EViews操作◇演示建立两种EViews工作文件，（1）混合数据型工作文件（file：5panel02），（2）面板数据型工作文件（file：6panel_02）。◇画散点图，（1）画个体符号不同的散点图，（2）画截面符号不同的散点图，（人均消费，file：5panel02a）◇配回归直线（食品支出，file：7panel05）。◇估计（Estimation）窗口介绍，◇各种面板数据模型的估计操作。混合、固定、随机效应，变斜率模型，动态面板。（file：5panel02）◇加AR项克服自相关。（人均消费，file：panel02）◇模型参数约束的检验（F、W、LR检验）。（人力资本，file：5panel04）◇决定模型类型的检验（F、Hausman检验）。（人均消费，file：panel02）◇预测（人均消费，file：panel02）◇单位根检验（人均消费，file：panel02）◇协整检验（人均消费，file：panel02、panel03）第第44章面板数据模型章面板数据模型7面板数据分析的EViews操作可以建立两种EViews工作文件，（1）混合数据型工作文件，（2）面板数据型工作文件。利用1996~2002年15个省级地区城镇居民家庭年人均消费性支出和年人均收入数据（不变价格数据）介绍面板数据模型估计步骤。（1）混合数据型工作文件1．用EViews6.0建立混合数据型工作文件、估计模型。首先建立一般年度工作文件（19962002）。（file：6pool02）在打开工作文件窗口的基础上，点击EViews主功能菜单上的Object键，选NewObject功能（如图1），从而打开NewObject（新对象）选择窗（如图2）。在TypeofObject选择区选择Pool（合并数据库），并在NameofObject选择区为混合数据库起名Pool1（初始显示为Untitled）。点击图2中OK键，从而打开混合数据库（Pool）窗口。图1图2在窗口中输入15个地区的标识AH（安徽）、BJ（北京）、…、ZJ（浙江），如图3。图3（2）定义序列名并输入数据。在新建的混合数据库（Pool）窗口的工具栏中点击Sheet键（符号？表示与CP和IP相连的15个地区标识名）如图4。点击OK键，从而打开混合数据库（Pool）窗口（图5）。（点击Edit+-键，使EViwes处于可编辑状态）可以用键盘输入数据，也可以用复制和粘贴的方法输入数据。注意：图5所示为以个体为序的阵列式排列（stackeddata）。点击Order+-键，还可以变换为以截面为序的阵列式排列。图4图5输入完成后的情形见图6。点击PanelGener或Quick/GenerateSeriesbyEquation健，可以通过公式用已有的变量生成新变量（注意：输入变量时，不要忘记带变量后缀“？”）。图6第第44章面板数据模型章面板数据模型（2）画个体符号不同的散点图，（人均消费，file：panel02）截面符号不同的散点图与此相仿。（5panel02c，graph2）2,0003,0004,0005,0006,0007,0008,0009,00010,00011,0002,0004,0006,0008,00010,00012,00014,000IPSER01SER02SER03SER04SER05SER06SER07SER08SER09SER10SER11SER12SER13SER14SER15（3）配回归直线（食品支出，file：5expend-zhang-2）。图5倒数拟合（file：5expend-zhang-2）图62次多项式拟合-2000-1000010002000300040005000040008000120001600020000I1F1F1vs.InverseofI1010002000300040005000040008000120001600020000I1F1F1vs.Polynomial(degree=2)ofI101,0002,0003,0004,0005,00002,0006,00010,00014,00018,000log(income)food5.56.06.57.07.58.08.59.06.06.57.07.58.08.59.09.510.0LOG(CINCOME)LOG(Cfood)◇面板数据模型的估计操作。混合、固定、随机效应，不同斜率，动态面板模型在打开工作文件窗口的基础上，点击主功能菜单中的Objects键，选NewObject功能，从而打开NewObject（新对象）选择窗。在TypeofObject选择区选择Pool（混合数据库），点击OK键，从而打开Pool（混合数据）窗口（图8）。在窗口中输入15个地区标识（变量的后缀）AH（安徽）、BJ（北京）、…、ZJ（浙江）。◇加AR项克服自相关。（人均消费，file：panel02）◇模型参数约束的检验（F、W、LR检验）。（人力资本，file：5panel04）◇决定模型类型的检验（F、Hausman检验）。（人均消费，file：panel02）◇预测（人均消费，file：panel02）点击Estimation键，随后弹出PooledEstimation（混合估计）对话窗口。EViwes5.0对话窗口见图9。图9EViwes5.0面板模型估计窗口EViwes6混合估计（PoolEstimation）窗口见图10。混合估计窗口分为两个模块，Specification（设定）和Options（选择），基本功能与早期版本无本质区别。选项主要集中在Specification（设定）模块中。图10EViwes6面板模型估计窗口在EstimationMethod（估计方法）选项区内有三个选项框。（1）Cross-section（横跨个体）中包括None（不选），Fixed（固定），Random（随机）分别用来做非个体效应，个体固定效应和个体随机效应的设定（见图11）。（2）Period（时点）中也包括None（不选），Fixed（固定），Random（随机）三项选择分别用来进行非时点效应，时点固定效应或时点随机效应设定（见图12）。（3）Weight（权数）可以在5种加权方法中做选择（见图13）。图11图12图13在EViews5、6的随机效应模型估计结果窗口点击View键，选Fixed/RandomEffectsTesting/CorrelatedRandomEffect-HausmanTest功能，可以直接获得应该建立随机效应模型还是个体固定效应模型的Hausman检验结果。用EViwes可以估计固定效应模型（包括个体固定效应模型、时点固定效应模型和时点个体固定效应模型3种）、随机效应模型、带有AR(1)参数的模型、截面不同回归系数也不同的面板数据模型。用EViwes可以选择普通最小二乘法、加权最小二乘法（以截面模型的方差为权）、似不相关回归法估计模型参数。可以在Commoncoefficients选择窗和Crosssectionspecificcoefficients选择窗中填入AR(1)项。如果把AR(1)项填在Commoncoefficients选择窗中相当于假设模型有相同的自回归误差项，如果把AR(1)项填在Crosssectionspecificcoefficients选择窗中相当于假设模型有不同的自回归误差项。注意：如果把解释变量填入Crosssectionspecificcoefficients选择窗中，对应不同的解释变量将会得到不同的回归参数。估计过程中的缺省方法是等权（Noweighting）估计。还可以选择Crosssectionweights（按截面取权数）和SUR（似不相关回归）。第第44章面板数据模型章面板数据模型注意：（1）EViwes输出结果中没有给出描述个体效应的截距项相应的标准差和t值。（2）当对个体固定效应模型选择加权估计时，输出结果将给出加权估计和非加权估计两种统计量评价结果。（3）输出结果的联立方程组形式可以通过点击View选Representations功能获得。（4）点击View选WaldCoefficientTests…功能可以对模型的斜率进行Wald检验。例如c(1)=0.7。（5）点击View选Residuals/Table,Graphs,CovarianceMatrix,CorrelationMatrix功能可以分别得到按个体计算的残差序列表，残差序列图，残差序列的方差协方差矩阵，残差序列的相关系数矩阵。（6）点击Procs选MakeModel功能，将会出现估计结果的联立方程形式，进一步点击Solve键，在随后出现的对话框中可以进行动态和静态预测。第第44章面板数据模型章面板数据模型◇加AR项克服自相关。（人均消费，file：panel02）◇模型参数约束的检验（F、W、LR检验）。（人力资本，file：5panel04）◇决定模型类型的检验（F、Hausman检验）。（人均消费，file：panel02）◇预测（人均消费，file：panel02）第第44章面板数据模型章面板数据模型（2）面板数据型工作文件。建立面板数据型工作文件（19962002）。（file：6panel02）第第44章面板数据模型章面板数据模型Object/newObject/series/cp,ip（不必写问号？）输入数据。第第44章面板数据模型章面板数据模型混合数据型工作文件（Pool）和面板数据型工作文件（panel）的对比混合数据型工作文件（Pool）画图面板数据型工作文件（panel）画图7.88.08.28.48.68.89.09.29.48.08.28.48.68.89.09.29.49.6LOG(IPCROSS)LOG(CP1996)LOG(CP1997)LOG(CP1998)LOG(CP1999)LOG(CP2000)LOG(CP2001)LOG(CP2002)7.88.08.28.48.68.89.09.29.48.08.28.48.68.89.09.29.49.6LOG(IP)LOG(CP)面板数据型工作文件（面板数据型工作文件（panelpanel）的估计窗口）的估计窗口点击点击QuickQuick键选键选EquationEstimationEquationEstimation，专有模型类型模块，专有模型类型模块PanelOptionPanelOption。。混合数据型工作文件（Pool）和面板数据型工作文件（panel）的对比面板数据型工作文件（Panel）画图混合数据型工作文件（Pool）画图第4章结束.