中考专题-一线三等角模型

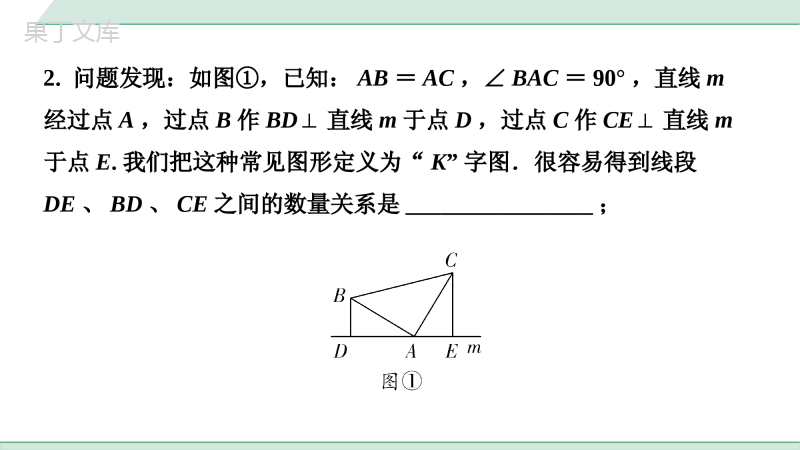
中考专题一线三等角模型模型一一线三等角基本模型(锐角、钝角)模型应用1.如图，在△ABC中，点D是BC上一点，连接AD，点E是AD上一点，连接BE，若∠BAC＝∠BED，∠BAC＋∠ADC＝180°，AE＝1，BE＝CD＝2，则DE的长是__．第1题图32.问题发现：如图①，已知：AB＝AC，∠BAC＝90°，直线m经过点A，过点B作BD⊥直线m于点D，过点C作CE⊥直线m于点E.我们把这种常见图形定义为“K”字图．很容易得到线段DE、BD、CE之间的数量关系是________________；【解法提示】∵BD⊥直线m，CE⊥直线m，∴∠BDA＝∠AEC＝90°，∵∠BAC＝90°，∴∠BAD＋∠CAE＝90°，∵∠BAD＋∠ABD＝90°，∴∠CAE＝∠ABD，在△ADB和△CEA中，∴△ADB≌△CEA(AAS)；∴AE＝BD，AD＝CE，∴DE＝AE＋AD＝BD＋CE.BDAAECABDCAE,ABCA很容易得到线段DE、BD、CE之间的数量关系是_____________；DE＝BD＋CEBDAAECABDCAE,ABCA线段DE、BD、CE之间的数量关系仍然成立．证明：设∠BDA＝∠BAC＝α，∴∠ABD＋∠BAD＝∠BAD＋∠CAE＝180°－α，∴∠CAE＝∠ABD，拓展探究：如图②，若AB＝AC，∠BAC＝∠BDA＝∠AEC，则线段DE、BD、CE之间的数量关系还成立吗？如果成立，请证明；在△ADB和△CEA中，∴△ADB≌△CEA(AAS)，∴AE＝BD，AD＝CE，∴DE＝AE＋AD＝BD＋CE；BDAAECABDCAEABCA,BDAAECABDCAEABCA,由(2)知，△ADB≌△CEA，∴BD＝AE，AD＝CE，∠DBA＝∠CAE，△ABF和△ACF均为等边三角形，∴∠ABF＝∠CAF＝∠BFA＝60°，AF＝BF，∴∠DBA＋∠ABF＝∠CAE＋∠CAF，∴∠DBF＝∠FAE，解决问题：如图③，若AB＝AC，∠BAC＝∠BDA＝∠AEC＝120°，点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，BD＝2，CE＝4，求△DEF的周长．在△DBF和△EAF中，∴△DBF≌△EAF(SAS)，∴DF＝EF，∠BFD＝∠AFE，∴∠DFE＝∠DFA＋∠AFE＝∠DFA＋∠BFD＝∠BFA＝60°，∴△DEF为等边三角形，∴△DEF的周长＝3DE＝3(AE＋AD)＝3(BD＋CE)＝3×(2＋4)FBFAFBDFAEBDAE,FBFAFBDFAEBDAE,模型分析已知A、P、B三点共线，且∠1＝∠2＝∠3.(1)点P在线段AB上图①图②(2)点P在线段AB的延长线上图③图④结论：①△ACP∽△BPD；②当AC＝BP或AP＝BD或CP＝PD时，△CAP≌△PBD.如图①，当点P为线段AB的中点时，连接CD，则△ACP∽△BPD∽△PCD图①模型二一线三垂直(直角)模型应用3.如图，A、B、C三点在同一条直线上，∠A＝∠C＝90°，AB＝CD，添加下列条件，不能判定△EAB≌△BCD的是()A.∠E＋∠D＝90°B.AC＝AE＋CDC.EB＝BDD.∠EBD＝60°第3题图D4.如图，在矩形ABCD中，E是BC的中点，DF⊥AE，垂足为F.若AB＝12，BC＝10，则DF的长为()A.B.C.D.9013100131101312013第4题图D90131001311013120135.如图，在正方形ABCD中，点E、F、G分别在AB，BC，CD上，且∠EFG＝90°.若AB＝9，AE＝2，CF＝3，则CG的长为__．第5题图187187证明：∵∠BAC＝90°，BE⊥AD，∴∠AEB＝90°，∠B＋∠BAF＝∠BAF＋∠CAF＝90°，∴∠B＝∠CAF，∵CF⊥AD，∴∠CFA＝∠AEB＝90°，6.(2021南充)如图，∠BAC＝90°，AD是∠BAC内部一条射线，若AB＝AC，BE⊥AD于点E，CF⊥AD于点F.求证：AF＝BE.第6题图CFAAEBCAFBACBA,在△ACF和△BAE中，∴△ACF≌△BAE(AAS)，∴AF＝BE.第6题图CFAAEBCAFBACBA,7.点E是矩形ABCD边AB延长线上的一动点，在矩形ABCD外作RtECF△，其中∠ECF＝90°，过点F作FG⊥BC，交BC的延长线于点G，连接DF，交CG于点H.(1)发现如图①，若AB＝AD，CE＝CF，猜想线段DH与HF的数量关系；第7题图①解：DH＝HF；理由如下：∵四边形ABCD是矩形，AB＝AD，∴四边形ABCD是正方形，∴BC＝CD，∠ABC＝∠EBC＝∠BCD＝90°，∴CD⊥BC，第7题图①∵FG⊥BC，∠ECF＝90°，∴CD∥GF，∠CGF＝∠ECF＝∠EBC＝90°，∴∠GCF＋∠BCE＝90°，∠BCE＋∠BEC＝90°，∴∠GCF＝∠BEC，在△GCF和△BEC中，∴△GCF≌△BEC(AAS)，∴BC＝GF，∴CD＝GF，CGFEBCGCFBECCFCE,CGFEBCGCFBECCFCE,第7题图①∵CD∥GF，∴∠HDC＝∠HFG，∠HCD＝∠HGF，在△HCD和△HGF中，∴△HCD≌△HGF(ASA)，∴DH＝HF；HDCHFGCDGFHCDHGF,HDCHFGCDGFHCDHGF,(2)探究如图②，若AB＝nAD，CF＝nCE，则(1)中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由；第7题图②DH＝HF仍然成立；证明：∵四边形ABCD是矩形，FG⊥BC，∠ECF＝90°，∴∠CGF＝∠ECF＝∠EBC＝90°，∴∠FCG＋∠BCE＝90°，∠BCE＋∠CEB＝90°，∴∠FCG＝∠CEB，∴△FCG∽△CEB，∴，GFCFnBCCEGFCFnBCCE∵四边形ABCD是矩形，AD＝BC，AB＝nAD，∴，∴，∴GF＝CD，∵四边形ABCD是矩形，∴CD⊥BC，∵FG⊥BC，∴CD∥GF，∴∠HDC＝∠HFG，∠HCD＝∠HGF，在△HCD和△HGF中，∴△HCD≌△HGF(ASA)，第7题图②CDnBCGFCDBCBCHDCHFGCDGFHCDHGF,CDnBCGFCDBCBCHDCHFGCDGFHCDHGF,备用图(3)拓展在(2)的基础上，若射线FC过AD的三等分点，AD＝3，AB＝4，请直接写出线段EF的长．【解法提示】如解图，设射线FC交AD于点R，R∵四边形ABCD是矩形，∴AB＝CD＝4，AD＝BC＝3，∠RDC＝90°，RD∥CH，∵AB＝nAD，CF＝nCE，∴，∴CE＝CF，分两种情况讨论：ABnAD4334ABnAD4334①当AR＝AD时，∵AD＝3，∴AR＝1，DR＝2，在RtCDR△中，由勾股定理得，∵RD∥CH，DH＝HF，∴RC＝CF＝，∴CE＝，在Rt△CEF中，由勾股定理得；13CRDRCD22222425335254225EFCFCE222235552522备用图R13CRDRCD22222425335254225EFCFCE222235552522②当DR＝AD时，同理可得DR＝1，RC＝，CF＝RC＝，CE＝，在Rt△CEF中，由勾股定理得，综上所述，若射线FC过AD的三等分点，AD＝3，AB＝4，则线段EF的长为或.1317173174备用图R22223175171744EFCFCE5525174131717317422223175171744EFCFCE5525174模型分析已知A、B、C三点共线，且∠1＝∠2＝∠3＝90°.结论：图①，图③中：①△ABD∽△CEB；②当AB＝CE或AD＝CB或BD＝EB时，△ABD≌△CEB.图②中：①△AFD∽△CEB∽△GFB；②当AF＝CE或AD＝CB或FD＝EB时，△AFD≌△CEB模型迁移8.如图，已知抛物线y＝－2x2＋4x＋6与x轴交于A、B两点，与y轴交于点C，M为抛物线上一点，过点M作MN⊥y轴于点N，是否存在点M，使得△CNM∽△BOC？若存在，求出点M的坐标；若不存在，请说明理由．第8题图解：存在点M，使得△CNM∽△BOC.∵抛物线y＝－2x2＋4x＋6与x轴交于A、B两点，与y轴交于点C，∴令y＝0，即－2x2＋4x＋6＝0，解得x1＝－1，x2＝3，令x＝0，解得y＝6，∴A(－1，0)，B(3，0)，C(0，6)，∴OB＝3，OC＝6，第8题图设M(a，－2a2＋4a＋6)，当△CNM∽△BOC，点N在点C上方时，如解图，∴，即，解得a＝0(舍去)或a＝，∴M(，)，第8题图CNMNBOCOaaa22466367474558MNCNMNBOCOaaa22466367474558同理，当点N在点C下方时，如解图，，解得a＝0(舍去)或a＝，∴M(，)．综上所述，当△CNM∽△BOC时，点M的坐标为(，)或(，)．第8题图aaCNMNaBOCO26246=369494398MNNM7455894398aaCNMNaBOCO26246=369494398NM7455894398